实验5 稀疏矩阵-Toy模板网

这篇具有很好参考价值的文章主要介绍了实验5 稀疏矩阵。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实验5 稀疏矩阵

注意

数据类型请使用int,本题中所有运算的结果均视作对int型自然溢出
可以使用 vector 等 STL 中的容器保存稀疏矩阵元素，减少不必要的bug
各操作需在稀疏矩阵上进行，充分考虑数据的稀疏性， 不得直接或间接转换为二维数组形式计算 ，否则取消成绩

题目描述

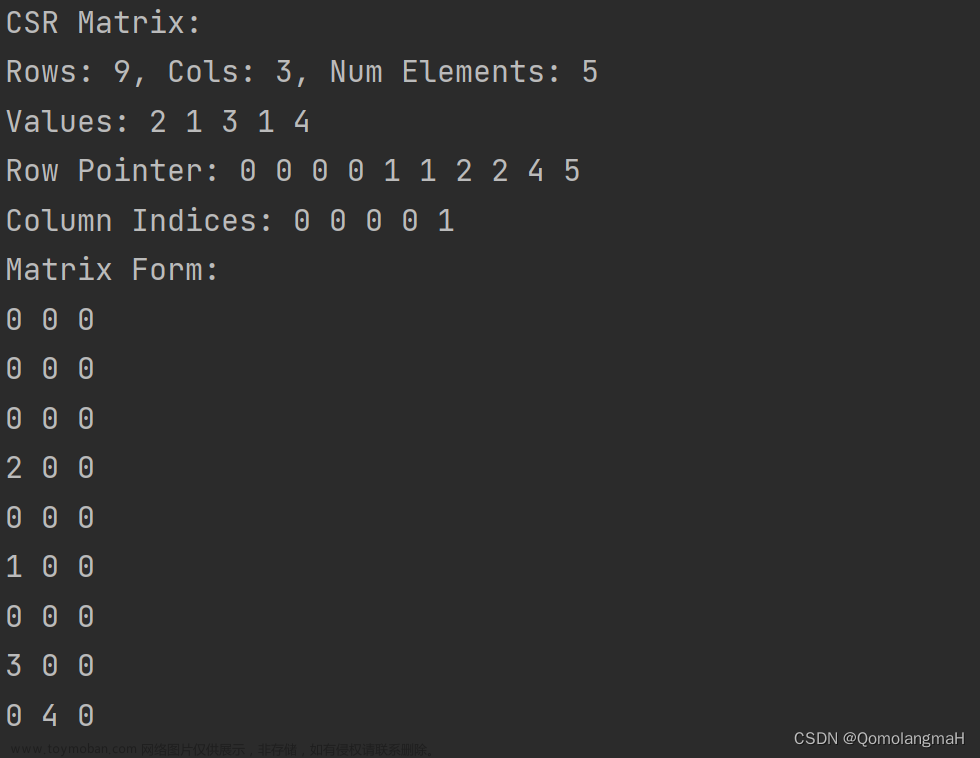
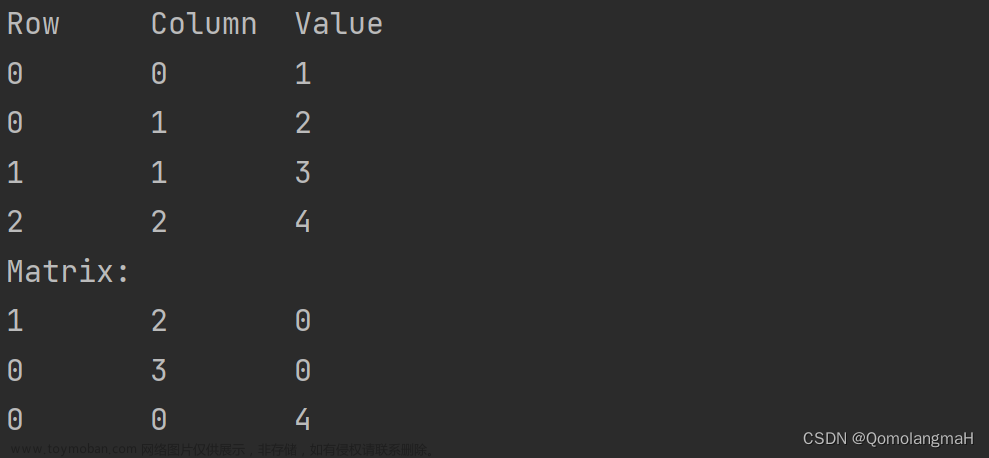
创建 稀疏矩阵类 （参照课本 MatrixTerm 三元组定义） ,采用行主顺序把稀疏矩阵非0元素映射到一维数组中,提供操作:两个稀疏矩阵相加、两个稀疏矩阵相乘、稀疏矩阵的转置、输出矩阵。
键盘输入矩阵的行数、列数;并按行优先顺序输入矩阵的各元素值,建立矩阵;
对建立的矩阵执行相加、相乘、转置的操作,输出操作的结果矩阵。

操作描述

为方便操作描述,我们假设存在一个矩阵 P,下列各操作实际为对矩阵 P 的操作。
重置矩阵 :
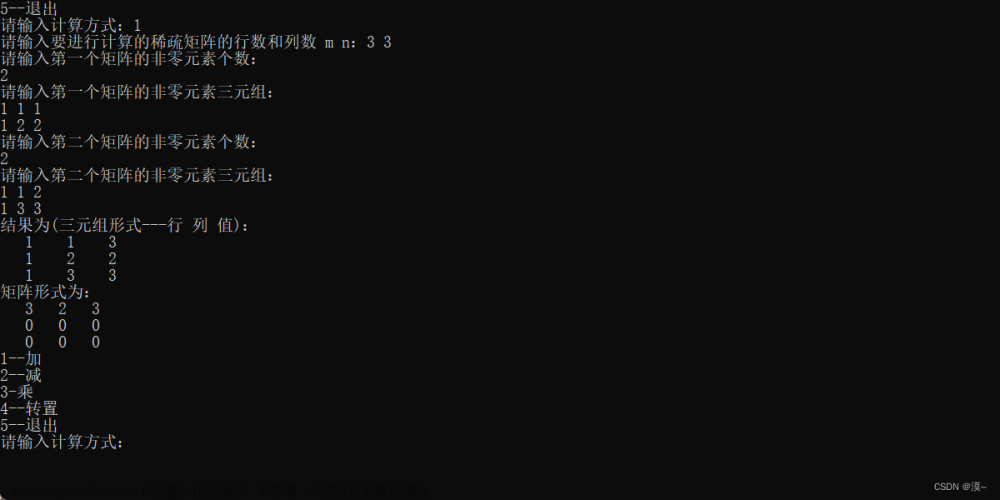
1
矩阵的行数n 矩阵的列数m
[n行m列表示矩阵中的所有元素]
即重置矩阵 P 的尺寸为 n 行 m 列,且随后按行优先顺序输入矩阵 P 的各个元素。
矩阵乘法:
2
矩阵的行数矩阵的列数
矩阵中非零元素个数t
[t行表示矩阵中非零元素]
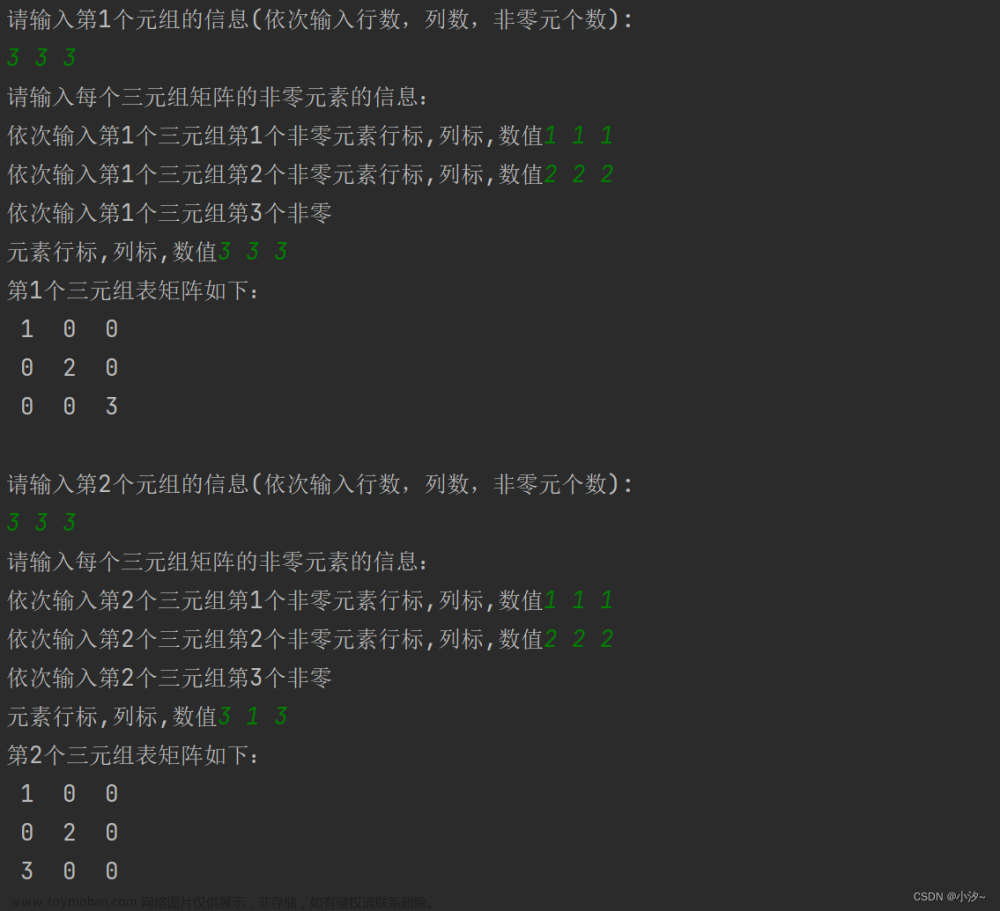
t 行非零元素已按行优先顺序给出，矩阵中非零元素的表示为 x y v，其中 x 表示行序号，y 表示列序号，v 表示非零元素值，行列序号从 1 开始。
设输入的矩阵为 Q,若 PxQ 运算合法,则将 PxQ 的结果矩阵赋给 P,若不合法,则将 Q 赋给 P,同时输出 -1。
矩阵加法:
3
矩阵的行数矩阵的列数
矩阵中非零元素个数t
[t行表示矩阵中非零元素]
t 行非零元素已按行优先顺序给出，矩阵中非零元素的表示为 x y v，其中 x 表示行序号，y 表示列序号，v 表示非零元素值，行列序号从 1 开始。
设输入的矩阵为 Q,若 P+Q 运算合法,则将 P+Q 的结果矩阵赋给 P,若不合法,则将 Q 赋给 P,同时输出 -1。
输出操作:
4
设当前矩阵 P 的尺寸为 n 行 m 列,第一行输出矩阵 P 的行数和列数，随后 n 行按行优先顺序输出矩阵 P,每行 m 个数字,来表示当前的矩阵内容，每行数字之间用空格分隔。
转置操作:
5
设当前矩阵 P 的尺寸为 n 行 m 列，将其转置为 m 行 n 列的矩阵，无需输出。

思路与探讨

数组和矩阵

笔记补充：详细写了数组和矩阵的相关知识

本次实验参考第七章稀疏矩阵的相关描述，但在具体实现时做了简化。比如没用迭代器和arrayList。

整体思路描述

定义一个三元组结构体，用于存储稀疏矩阵
定义一个稀疏矩阵类，并依次定义重置，乘法，加法，输出，转置等相关操作
而后对相关操作依次进行实现
最后设置主函数，通过条件语句设置相关操作的触发条件，完成实验。

细节思路补充

关键点

定位每一行（列）第一个非0元素的索引可以辅助快速准确读取三元组里的数据。
为此，需要附设两个数组，num 和 Index，分别用于记录存储在三元组中的稀疏矩阵 a 中每一行（列）的非 0 元素个数和每一行（列）第 1 个非0 元素在三元组中的索引。

以上是稀疏矩阵乘法和转置的核心关键点。
可提高程序针对稀疏矩阵运算效率。

//计算a每行中的非0元素个数
for (int i = 1; i <= a.Rows; i++)
	num[i] = 0;//每行计数清零 
for (int i = 0; i < a.Terms; i++)
{
	if (a.element[i].value != 0)//遍历非零 
		num[a.element[i].row]++;//计数得第i行对应非零元素个数 
}
//求出a中每一行第1个非0元素的对应索引
Index[1] = 0;
for (int i = 2; i <= a.Terms; i++)
	Index[i] = Index[i - 1] + num[i - 1];//第i行第一个非零元素索引

乘法思路

有效性检验
借助上述定位法由公式计算乘法结果
将结果中的非0元素导出三元组

矩阵加法

有效性检验
使用it和ib，从左至右依次扫描两个矩阵中的非0元素。
当it和ib都未扫描完成时，循环：
- 计算it所指的元素和ib所指的元素按行主次序的索引
  - tIndex = P中的it所指的元素索引
  - bIndex = Q中ib所指的元素索引
    - 元素索引——（元素的行下标-1）* 列数+元素的列下标
  - 判断tIndex > bIndex 还是tIndex=bIndex，确定it所指的元素是在ib所指的元素之前，之后还是进行相加运算,并只在和不为0时才加入C(结果矩阵三元组）。
复制剩余元素

矩阵转置

设置转置矩阵特征
计算待转置矩阵中每一列非0元素的个数
确定矩阵第i列第1个非0元素的对应索引
实施从*this到b的转置复制

若已看懂思路，试着自己写~文章来源地址https://www.toymoban.com/news/detail-714939.html

实现代码

#include <iostream>
using namespace std;

struct matrixTerm 
{//三元组结构体定义 
    int row, col, value;
    matrixTerm& operator=(matrixTerm& x) 
    {//运算符重载 ，赋值*this = x 
        row = x.row;
        col = x.col;
        value = x.value;
        return *this;
    }
};
const int maxsize = 199999;//新matrixTerm创建最大容量设定 

class sparseMatrix//稀疏矩阵类定义 
{
private:
    int Rows;//行 
	int Cols;//列
	int Terms;//非零元素个数 
    matrixTerm * element;//用来存非零元素的数组 
    int maxSize;//数组最大容量 
public:
    sparseMatrix(int n,int m)//构造函数
	{
		element = new matrixTerm[maxsize];
        Rows = n;
        Cols = m;
        Terms= 0;
	} 
    ~sparseMatrix(){ delete[] element; }//析构函数 
    sparseMatrix& operator=(sparseMatrix& a)
	{//运算符重载 ，赋值*this = a 
		Rows = a.Rows;
        Cols = a.Cols;
        Terms = a.Terms;
        maxSize = a.maxSize;
        for (int i = 0; i < Terms; i++)
            element[i] = a.element[i];
        return *this;
	} 
	void inputAelement(int x,int y,int v);//辅助函数——非0值输入  
    void initial(int n,int m);//重置1
    int multiply(sparseMatrix& a); //乘法2 
    int add(sparseMatrix& a);//加法3 
    void output();//输出4 
    void transpose();//转置5 
};

 //辅助函数——非0值输入，更新三元组 
void sparseMatrix::inputAelement(int x,int y,int v)
{
    matrixTerm New;
    New.row = x;//行序号 
    New.col = y;//列序号 
    New.value = v;//非零元素值 
    element[Terms] = New;
    Terms++;
}

//重置1 
void sparseMatrix::initial(int n,int m) 
{
    Rows = n;
    Cols = m;
    Terms = 0;
    for (int i = 1; i <= Rows; i++)
    {//按行优先顺序输入矩阵的各个元素 
        for (int j = 1; j <= Cols; j++) 
		{
            int b;
            cin >> b;
            if (b != 0) 
			{
                element[Terms].row = i;
                element[Terms].col = j;
                element[Terms].value = b;
                Terms++;
            }
        }
    }
}

//乘法2 
int sparseMatrix::multiply(sparseMatrix& Q)
{
	//有效性检验 
    if (Cols != Q.Rows)
    {//按矩阵乘法C[m,n]= P[m,k] ×Q[k,n]，需要有Cols=Q.Rows 
        *this = Q;
        return -1;
    }
    else
    {
    	//取乘数P的行和乘数Q的列构建结果sparseMatrix
        sparseMatrix C(Rows, Q.Cols); 
        int num[10000]; //每行非零元素的个数 
        int Index[10000]; //每行第一个非零元素对应的索引  
        int Answer[10000];//存放乘法结果  
        
        //每行计数清零 
        for (int i = 1; i <= Q.Rows; i++)
            num[i] = 0;
        //计数得第i行对应非零元素个数 
		for (int i = 0; i < Q.Terms; i++)
        {
            if (Q.element[i].value != 0) 
                num[Q.element[i].row]++;
        }
        //第i行第一个非零元素索引 
        Index[1] = 0;
        for (int i = 2; i <= Q.Terms; i++)
            Index[i] = Index[i - 1] + num[i - 1];
        
		//开始乘法计算C[m,n]= P[m,k] ×Q[k,n]
		int p = 0;
        for (int i = 1; i <= Rows && p < Terms; i++) 
        {
        	//赋初值0 
            for (int j = 1; j <= Q.Cols; j++)
                Answer[j] = 0; 
            while (p < Terms && element[p].row == i)//循环条件为仍有非零元素且第i行有非零元素 
            {
                int t = element[p].col; 
                if (num[t] != 0) //P有非0元素的行对应的Q里的列任有非0元素 
                {//如果都是0了，乘法所得也不会是非0，这个判断起简化作用 
                    for (int q = Index[t]; q < Index[t] + num[t]; q++)
                    	//计算对应i行每列的乘积 
                        Answer[Q.element[q].col] += element[p].value * Q.element[q].value;
                }
                //继续下一个非零元素 
                p++;
            }
            for (int k = 1; k <= Q.Cols; k++)
            {//结果中的非0元素导出三元组 
                if (Answer[k] != 0)
                {
                    C.element[C.Terms].value = Answer[k];
                    C.element[C.Terms].row = i;
                    C.element[C.Terms].col = k;
                    C.Terms++;
                }
            }
        }
        *this = C;
		return 0;    
    }
}

//加法3
int sparseMatrix::add(sparseMatrix& Q)  
{
    if (Q.Cols != Cols || Q.Rows != Rows) //根据矩阵加法规则，行列不等不符合 
	{
        *this = Q;
        return -1;
    }
    else
	{
		sparseMatrix C(Rows, Cols);//设置结果矩阵的特征 
		int it = 0,ib = 0;	
		while(it != Terms && ib != Q.Terms)//遍历，把相关的项相加 
		{   //行主索引加上每一项的列数 
			int tIndex = (element[it]).row*Cols + (element[it]).col;
			int bIndex = (Q.element[ib]).row*Cols + (Q.element[ib]).col;
			if(tIndex < bIndex)
			{//Q项在后 
				C.element[C.Terms].col = element[it].col;
				C.element[C.Terms].row = element[it].row;
				C.element[C.Terms].value = element[it].value;
				it++;
		        C.Terms++;
			}	
			else if(tIndex == bIndex)
			{//两项在同一个位置 
				if((element[it]).value + (Q.element[ib]).value != 0)
				{//仅当相加后不为0时加入c 
					C.element[C.Terms].col = (element[it]).col;
					C.element[C.Terms].row = (element[it]).row;
					C.element[C.Terms].value = (element[it]).value + (Q.element[ib]).value;
					C.Terms++;
				}
				it++;ib++;
			}
			else 
			{
			    C.element[C.Terms].col = Q.element[ib].col;
				C.element[C.Terms].row = Q.element[ib].row;
				C.element[C.Terms].value = Q.element[ib].value;
				ib++;
				C.Terms++;
			}
		}
		//复制剩余项
		for(;it != Terms;it++)
		{
			C.element[C.Terms].col = element[it].col;
			C.element[C.Terms].row = element[it].row;
			C.element[C.Terms].value = element[it].value;
			C.Terms++;
		}
		for(;ib != Q.Terms;ib++)
		{
			C.element[C.Terms].col = Q.element[ib].col;
			C.element[C.Terms].row = Q.element[ib].row;
			C.element[C.Terms].value = Q.element[ib].value;
			C.Terms++;
		}
		*this = C;
		return 0;	
	}
}

//输出4 
void sparseMatrix::output()
{
    int i, j, k = 0;
    cout << Rows << " " << Cols << endl;
    for (i = 0; i < Rows; i++)//遍历输出 
	{
        for (j = 0; j < Cols; j++)
		{
            if (k < Terms && element[k].row == i + 1 && element[k].col == j + 1)
			{
                cout << element[k].value << " ";
                k++;
            }
            else
			    cout <<0<< " ";
        }
        cout << endl;
    }
}

//转置5
void sparseMatrix::transpose() 
{
    //设置转置矩阵特征
    sparseMatrix b(Cols,Rows); 
    b.Terms = Terms;
    b.Cols = Rows;
    b.Rows = Cols;
    //初始化
    int* colSize = new int[Cols + 1];//矩阵第i列的非零元素个数 
    int* rowNext = new int[Cols + 1];//矩阵第i列第一个非零元素索引  

    //计算待转置矩阵中每一列非0元素的个数
    for (int i = 1; i <= Cols; i++) 
        colSize[i] = 0;
    for (int i = 0; i < Terms; i++)
        colSize[element[i].col]++;
    //确定矩阵第i列第1个非0元素的对应索引
    rowNext[1] = 0;
    for (int i = 2; i <= Cols; i++)
        rowNext[i] = rowNext[i - 1] + colSize[i - 1];
    //上述几步和乘法中同理，提高程序针对稀疏矩阵运算效率 
      
    //实施从*this到b的转置复制
    for(int i = 0;i < Terms;i++)
    {
        int j = rowNext[element[i].col];
        //行列转置
        b.element[j].row = element[i].col;
        b.element[j].col = element[i].row;
        b.element[j].value = element[i].value; 
        rowNext[element[i].col] = rowNext[element[i].col] + 1;	
		//对应列rowNext索引+1，以防同一列有多个非零元素 (防撞） 
    }
    *this = b;
}

int main()
{
    sparseMatrix P(0,0);
    int w;//操作个数 
    int panduan = 0;//各种不合法输出工具变量 
    int n;//矩阵行数 
	int m;//矩阵列数 
	int t;//矩阵非0元素个数 
	int trans;//操作编码 
    cin>> w;
    for (int i = 0; i < w; i++) 
	{
        cin >> trans;
        if (trans == 1) 
		{//重置矩阵 
            cin >> n >> m;
            P.initial(n, m);
        }
        else if(trans == 2)
		{//矩阵乘法 
            cin >> n >> m;
            cin >> t;
            sparseMatrix Q1(n, m);
            for (int i = 0; i < t; i++) 
			{
				//Q矩阵非零元素的行、列序号及非0元素值 
                int x, y, v;
                cin >> x >> y >> v;
                Q1.inputAelement(x, y, v);
            }
            panduan = P.multiply(Q1);
            if(panduan == -1)
                cout << panduan << endl;
        }
        else if(trans == 3)
		{//矩阵加法 
            cin >> n >> m;
            cin >> t;
            sparseMatrix Q2(n, m);
            for (int i = 0; i < t; i++) 
			{
                int x, y, v;
                cin >> x >> y >> v;
                Q2.inputAelement(x, y, v);
            }
            panduan = P.add(Q2);
            if(panduan == -1)
                cout << panduan << endl;
        }
        else if (trans == 4) 
        	//输出操作 
		    P.output();
        else
        	//转置 
		    P.transpose();
    }
    return 0;
}