搜索与图论：染色法判定二分图-Toy模板网

这篇具有很好参考价值的文章主要介绍了搜索与图论：染色法判定二分图。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

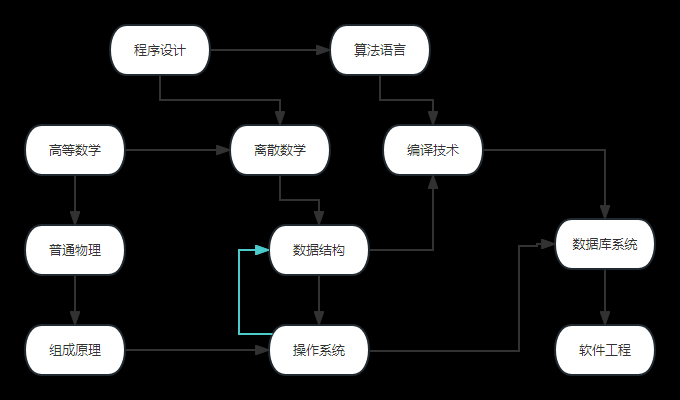
将所有点分成两个集合，使得所有边只出现在集合之间，就是二分图

二分图：一定不含有奇数个点数的环；可能包含长度为偶数的环，不一定是连通图

染色可以使用1和2区分不同颜色，用0表示未染色
遍历所有点，每次将未染色的点进行dfs, 默认染成1或者2
由于某个点染色成功不代表整个图就是二分图,因此只有某个点染色失败就能立刻break/return

染色失败相当于存在相邻的2个点染了相同的颜色，即点的个数的奇数个文章来源地址https://www.toymoban.com/news/detail-715047.html

染色法判定二分图：

#include <iostream>
#include <cstring>

using namespace std;
const int N = 1e5 + 10, M = 2e5 + 10; // 由于是无向图, 顶点数最大是N，那么边数M最大是顶点数的2倍
int e[M], ne[M], h[N], idx;//邻接表
int st[N];//该点的颜色

void add(int a, int b)
{
//头插法
    //如图 如1与2之间要有一条线，让2的ne为1，再让h[1]为2的索引。
    //这样h[1]就是1节点存的最后一个相连的点，如图就是7节点。
    //而在索引表内部，通过头插法的方式(即每次ne指向上一个点(h存的就是上一个点))，索引表为：7->4->2
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++;
}

bool dfs(int u, int color) 
{
    st[u] = color;

    for(int i = h[u]; i != -1; i = ne[i])
    {//遍历邻接表
        int j = e[i];
        if(!st[j]) //若还没颜色，则递归下去染色
        {
        //递归下去
            if(!dfs(j, 3 - color)) return false;//如果当前是3-2=1，则下一次是3-1=2，以此类推，奇数和偶数的点颜色不一样
        }
        //如果该点有颜色，则判断该点的颜色是否跟邻接表的头点颜色相同，相同则说明矛盾
        else if(st[j] == color) return false;
    }
    return true;
}

int main()
{
    int n, m;
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);
    while (m --)
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b,a);  // 无向图，a->b, b->a
    }

    bool flag = true;
    for(int i = 1; i <= n; i ++)
    {
        if(!st[i])
        {
            if(!dfs(i, 1))//如果返回FALSE，则说明有矛盾发生，flag赋为FALSE
            {
                flag = false;
                break;
            }
        }
    }
    if(flag) printf("Yes\n");
    else printf("No\n");
    return 0;
}

到了这里，关于搜索与图论：染色法判定二分图的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！