数据结构可以说是程序员常用,但大部分人不知其所以然的知识点,本文将对Hash、二叉搜索树、平衡二叉树、B-Tree、B+Tree几种数据做一下梳理和总结。
1、Hash 结构
1.1、关于 Hash 数据结构
Hash 本身是一个函数,又被称为散列函数,可以大幅提升检索数据的效率。
-
Hash 算法是通过某种特定性的算法(比如:MD5、SHA1、SHA2、SHA3)将输入转变为输出。
相同的输入永远可以得到相同的输出,假设输入内容有微小偏差,在输出中通常会有不同的结果。 -
Hash值的长度是固定的,而输入数据的可能性是无限的,这就会出现不同的输入数据映射到了相同的Hash值,这种现象就叫
Hash碰撞。 -
解决Hash碰撞的常见方案有开放寻址法和链表法。开放寻址法是在发生碰撞时,尝试寻找下一个可用的槽位来存储数据。
链表法则是将映射到同一个Hash值的数据存储在一个链表中,通过链表来解决碰撞问题。 -
当链表长度过长时,查询效率会降低,此时可以将链表转换为红黑树来提高查询效率。红黑树是一种自平衡的二叉查找树,能够保证最坏情况下的查询时间复杂度为O(log n),其中n为节点数量。

举例:如果想要验证两个文件是否相同,可以直接对比两个文件通过Hash函数计算出的结果,如两个文件通过Hash函数计算的结果一样,即文件相同,否则不同。
提高查询速度的数据结构,常见的有两类:
树,例如:平衡二叉树,查询、插入、修改、删除的平均时间复杂度都是O(log2N).哈希,例如:HashMap,查询、插入、修改、删除的平均时间复杂度都是O(1) ;(key,value)
采用 Hash 进行检索效率非常高,基本都是一次检索就能找到数据,B+Tree 需要自顶向下依次查找,多次访问节点才能找到数据,中间需要多次 I/O 操作,从效率上来将 Hash 比 B+Tree 更快。
Hash 索引适用的存储引擎如表所示:
| 索引/存储引擎 | InnoDB | MyISAM | Memory |
|---|---|---|---|
| Hash 索引 | 不支持 | 不支持 | 支持 |
Hash 索引的使用场景:
-
① 当字段的重复度低,且经常需要进行
等值查询时,采用 Hash 索引是个不错的选择。 -
② Redis 存储的核心就是 Hash 表。
-
③ InnoDB 提供自适应 Hash 索引 (Adaptive Hash Index)
1.2、InnoDB索引为啥不选 Hash 结构
Hash结构效率高,那为啥InnoDB的索引结构要设计成树型呢?
- 原因①,
Hash索引仅能满足 (=)(<>)和 in 查询。如果进行 范围查询,时间复杂度会退化为O(n),树型结构的有序特性,依然能保持 O(log2N) 的高效率。 - 原因②,
Hash索引有一个缺陷,数据的存储是没有顺序的,在 ORDER BY 的情况下,使用 Hash 索引还需要对数据重新排序。 - 原因③,对于联合索引而言,Hash值是将联合索引键合并后一起来计算,无法对单独的一个键或几个索引键进行查询。
- 原因④,对于等值查询而言,通常 Hash 索引的效率更高,
但如果索引列的重复值很多,效率就会降低。因为当遇到 Hash 冲突时,需要遍历桶中的行指针来进行比较,找到查询的关键字,非常耗时。故 Hash 索引常不会用到重复值多的列上,比如 性别、年龄等。
1.3、关于InnoDB 提供自适应 Hash 索引 (Adaptive Hash Index)
如果某个数据经常被访问,当满足一定条件时,会将这个数据页的地址存放到 Hash 表中,下次查询的时候,就会直接找到这个数据页所在的位置。采用自适应 Hash 索引的目的就是,方便根据 SQL 的查询条件,加速定位到叶子节点,特别是当 B+Tree 比较深,层级比较多时,自适应Hash能显著提高数据的检索效率。
-- 查询是否开启 自适应Hash索引,默认为 ON ,开启.
show variables like '%adaptive_hash_index%';

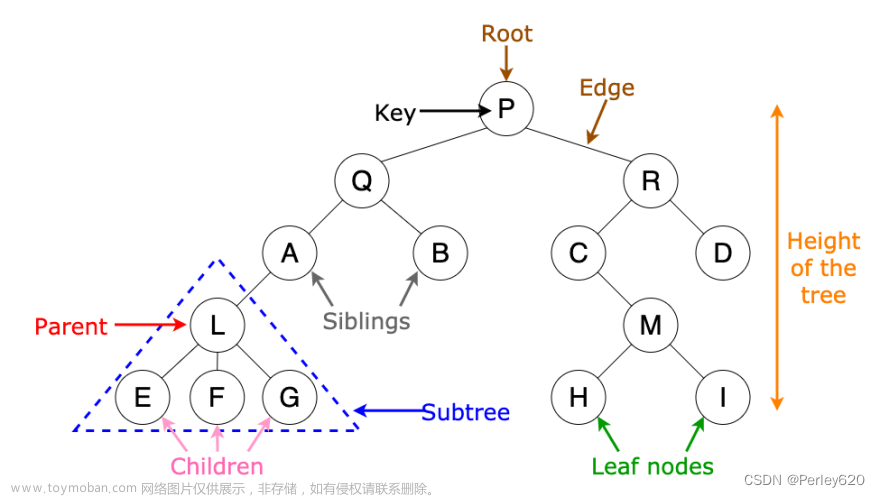
2、二叉搜索树
如果我们利用二叉树作为索引结构,那么磁盘的IO次数和索引树的高度是相关的。
二叉搜索树(二叉查找树)的特点:
一个节点只能有两个子节点,也就是一个节点度不能超过2.-
左子节点 < 本节点;右子节点 >= 本节点,比我大的向右,比我小的向左。
二叉搜索树的查找规则:
二叉搜索树(Binary Search Tree),搜索某个节点和插入节点的规则一样,假设搜索插入的数值为key:
- ① 如果 key 大于根节点,则在右子树中进行查找;
- ② 如果 key 小于根节点,则在左子树中进行查找;
- ③ 如果 key 等于根节点,也就是找到了这个节点,返回根节点即可。

二叉查找树可能退化成一条链表,查找数据的时间复杂度为O(N),如下图:
3、平衡二叉树(AVL树 )
为解决二叉搜索树可能退化成链表的问题,就出现了平衡二叉树(Balanced Binary Tree),又称为 AVL 树(有别于 AVL 算法),它是在二叉搜索树的基础上增加了一些约束:平衡二叉树是一课空树,或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一颗平衡二叉树。
常见的平衡二叉树包含:平衡二叉搜索树、红黑树、数堆、伸展树。一般平衡二叉树指的就是平衡二叉搜索树,搜索的时间复杂度为O(log2n),数据查询的时间主要依赖于磁盘的 I/O次数,当n 越大,查询越复杂。

每访问一次节点就需要进行一次磁盘I/O操作,以上图示例来讲,需要进行4次I/O操作。虽然平衡二叉树的效率高,但是树的深度比较高时,也意味着磁盘I/O操作次数多,就会影响整体数据查询的效率。
4、B-Tree(B树)
B树(Balance Tree)也就是多路平衡查找树,简写为 B-Tree(这里的横杠是连接符,而不是减号)。B-Tree 的高度远小于平衡二叉树的高度。B-Tree 关键点如下:
-
B-Tree 在插入、删除节点的时候,如果导致树不平衡,就通过
自动调节节点的位置来保持树的自平衡。 -
关键字集合分布在整棵树中,如果一个磁块包括了x个关键字,那指针数为x+1,
叶子节点和非叶子节点都存放数据。搜索有可能在非叶子节点结束。 -
搜索性能等价于在关键字全集内做一次二分查找。
-
对于一个M阶(每个节点最多可以包括M个子节点)的B-Tree,根节点的儿子数的范围是[2,M],且所有叶子节点位于同一层。

假设查询关键字为 8 的数据。
- ① 与根节点的关键字26 和 36 比较,8 小于26 ,取磁块1的P1指针向下级节点查找。
- ② 按磁块1的P1指针找到磁块2,比对关键字 6 和 21,8大于6且小于21,取取磁块2的P2指针向下级节点查找。
- ③ 按磁块2的P2指针找到磁块6,对比磁块6的关键字8和18,找到关键字8.
在B-Tree 的搜索中,是把数据读取出来,然后在内存中进行比较,那比较的时间可忽略不计。读取磁盘块本身需要进行I/O操作,其消耗的时间比在内存中进行比较需要的时间较多,是数据查找用时的重要因素。B-Tree相比于平衡二叉树来说,磁盘I/O操作要少效率高,只要树的高度足够低,I/O次数足够少,就可以提高查询性能。
5、B+Tree (B+树)
5.1、B+Tree 结构
B+Tree 是一种多路搜素树,基于B-Tree做出了改进。主流的 DBMS都支持 B+Tree 的索引方式。B+Tree相比于B-Tree在查询效率、磁盘读写性能和范围查询方面更具优势,B+Tree 比 B-Tree 更适合文件索引系统。

B+Tree和B-Tree的区别主要体现在以下三个方面:
-
① 内部节点存储数据的方式:B-Tree的每个内部节点都存储数据,而B+Tree的内部节点并不存储数据,只作为索引使用,数据都存储在叶子节点上。因为B+Tree只在叶子节点存储数据,所以在查询时稳定性更好,且查询速度更快。
-
② 叶子节点的链接方式:B+Tree的叶子节点之间通过指针连接,形成一个有序链表,便于进行范围查询。而B-Tree的叶子节点并没有相连,B-Tree 做范围查询时,需要通过中序遍历才能实现。在范围查询上,B+Tree 的效率比 B-Tree 高。
-
③ 磁盘读写性能:B+Tree相比于B-Tree,在磁盘读写性能上更有优势。这是因为B+Tree的内部节点并没有指向关键字具体信息的指针,所以其内部节点相对B-Tree更小,如果把内部节点和叶子节点存放在同一块磁盘内,那么盘块容纳的节点数目比B-Tree更多,一次性读入内存中的需要查找的关键字也就越多,相对来说IO读写次数也就降低了。
5.2、B+Tree 相关思考题
1、为了减少IO,B+Tree 索引树会一次性加载吗?
- ① 数据库索引存储在磁盘上,如果数据量过大,必然会导致索引的大小也会很大,超过几个G.
- ② 当利用索引查询时,是不可能将全部几个G 的索引数据,全都加载到内存中的。只能逐一加载每个磁盘页,因此磁盘页对应着索引树的节点。
2、B+Tree 的存储能力如何?为何说一般查找行记录,最多只需要 1~3次磁盘IO ?
InnoDB 存储引擎中数据页的大小默认为 16KB,一般表的主键类型为 int(占4个字节)或 bigint(占8个字节),指针类型一般也为4或8个字节,所以一个根节点或内节点的数据页(B+Tree中的一个节点)中大概存储 16KB/(8B+8B) = 1K 个键值。估算一下,就当K 的取值为10^3,那一个深度为3 的B+Tree 索引可以维护的数据为 10^3 * 10^3 * 10^2 = 1亿 条记录(这里假设一个叶子节点的数据页可以存 100 条行记录数据)。
实际情况中每个节点可能不会填充满,所以
在数据库中,B+Tree 的高度一般都在 2~4 层。MySQL 的InnoDB 存储引擎在设计时,将根节点常驻内存,也就是说查找某一键值的行记录时,最多只需要1~3次磁盘 IO 操作。
3、为什么说B+Tree 比 B-Tree 更适合实际应用中,操作系统的文件索引和数据库索引?
B+Tree 的磁盘读写代价更低B+Tree 的内部节点,并没有指向关键字具体信息的指针,故其内部节点相对B-Tree 更小。通俗来说,就是B-Tree每个层级的节点都存放的行数据,但是B+Tree 只有在叶子节点存放行数据,内节点存放主键或非聚簇索引字段,所以一般情况来讲相同的数据体量,B+Tree的层级会低,磁盘IO操作次数更少,磁盘读写代价更低。
B+Tree 的查询效率更稳定B+Tree 的叶子节点才会有用户记录行数据,所以任何关键字的查找,必须走一条从根节点到叶子节点的路,所有关键字查询的路径长度相同,导致每一个数据的查询效率相当。
4、Hash 索引和 B+Tree 索引的区别?
① Hash 索引不能进行范围查询,B+Tree 可以。
② Hash 索引不支持联合索引的最左原则(即联合索引的部分索引无法使用),B+Tree 可以。
③ Hash 索引不支持 ORDER BY 排序,B+Tree 可以(B+Tree索引数据是有序的)。
④ Hash 索引不支持模糊查询,B+Tree 使用LIKE进行模糊查询时, LIKE 后面后模糊查询(比如%结尾)可以起到优化作用。
⑤ InnoDB 不支持哈希索引,但提供自适应 Hash 索引 (Adaptive Hash Index)。
5、Hash 索引和 B+Tree 索引是在键索引时,手动指定的吗?
对于MySQL而言,针对 InnoDB 和 MyISAM 存储引擎,都会默认采用 B+Tree 索引,无法使用 Hash 索引。InnoDB 提供的自适应 Hash 是不需要手动指定的。如果 Memory/Heap 和 NDB 存储引擎,是可以进行选择 Hash 索引的。
系列文章:文章来源:https://www.toymoban.com/news/detail-715068.html
一: 《搞懂 MySql 的架构和执行流程》
二: 《从InnoDB索引的数据结构,去理解索引》
三: 《从 Hash索引、二叉树、B-Tree 与 B+Tree 对比看索引结构选择》
四: 《MySQL 的索引分类和设计原则》
五: 《MySQL 优化思路篇》
六: 《理解MySQL的日志 redo、undo、binlog》
七: 《并发事务下,不同隔离级别可能出现的问题》
八: 《多维度梳理 MySQL 锁》
九: 《MySQL 之多版本并发控制 MVCC》
.文章来源地址https://www.toymoban.com/news/detail-715068.html
到了这里,关于从 Hash索引、二叉树、B-Tree 与 B+Tree 对比看索引结构选择的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!