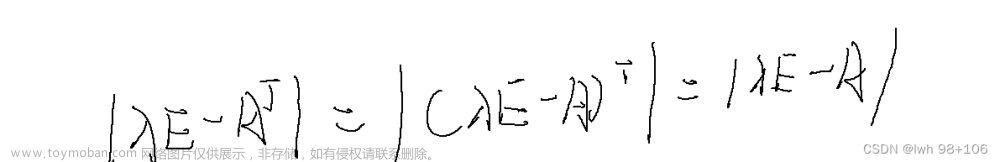性质 1 若 λ \lambda λ 是 A \boldsymbol{A} A 的特征值,当 A \boldsymbol{A} A 可逆时, 1 λ \frac{1}{\lambda} λ1 是 A − 1 \boldsymbol{A}^{-1} A−1 的特征值。文章来源:https://www.toymoban.com/news/detail-715194.html
证明 因为 λ \lambda λ 是 A \boldsymbol{A} A 的特征值,所以有 p ≠ 0 \boldsymbol{p} \ne 0 p=0 使 A p = λ p \boldsymbol{A} \boldsymbol{p} = \lambda \boldsymbol{p} Ap=λp。于是,当 A \boldsymbol{A} A 可逆时,因为 A p = λ p \boldsymbol{A} \boldsymbol{p} = \lambda \boldsymbol{p} Ap=λp,所以
p = λ A − 1 p \boldsymbol{p} = \lambda \boldsymbol{A}^{-1} \boldsymbol{p} p=λA−1p
因为 p ≠ 0 \boldsymbol{p} \ne 0 p=0,所以 λ ≠ 0 \lambda \ne 0 λ=0。从而上式两边可以同除 λ \lambda λ,有
A − 1 p = 1 λ p = λ − 1 p \boldsymbol{A}^{-1} \boldsymbol{p} = \frac{1}{\lambda} \boldsymbol{p} = \lambda^{-1} \boldsymbol{p} A−1p=λ1p=λ−1p
从而 1 λ \frac{1}{\lambda} λ1 是 A − 1 \boldsymbol{A}^{-1} A−1 的特征值。得证。文章来源地址https://www.toymoban.com/news/detail-715194.html
到了这里,关于线性代数|证明:矩阵特征值的倒数是其逆矩阵的特征值的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!