三元组（C++ 实现矩阵快速转置)-Toy模板网

这篇具有很好参考价值的文章主要介绍了三元组（C++ 实现矩阵快速转置)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

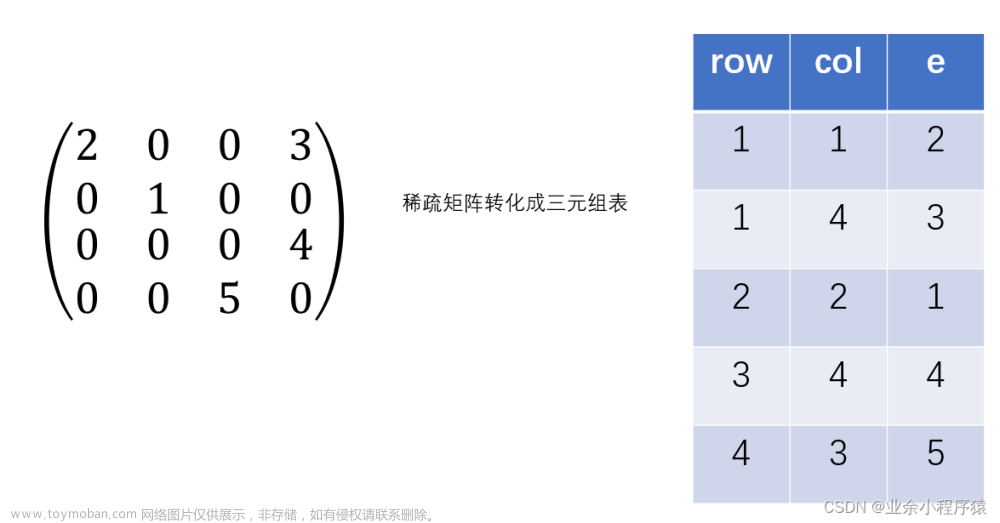
三元组稀疏矩阵是一种高效存储稀疏矩阵的方法。它通过记录矩阵中非零元素的行、列和值来表示一个稀疏矩阵。我们在三元组里存储的是每个元素的行、列以及值。

题目：

任意输入一个稀疏矩阵M，用三元组顺序表压缩存储该稀疏矩阵M，然后求其转置矩阵T，并输出转置矩阵T。

思路：

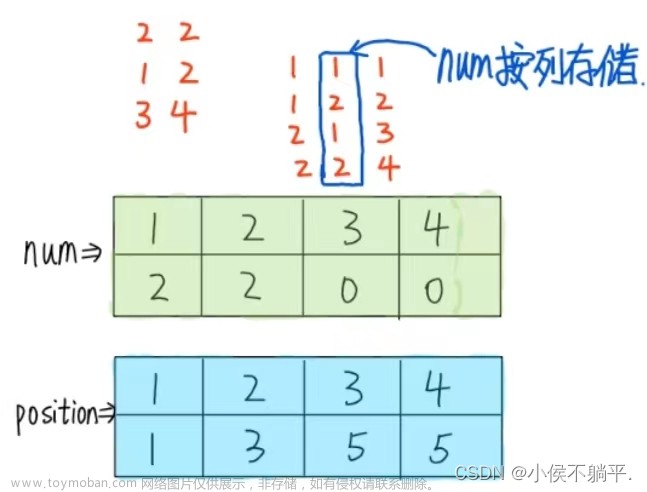
1、这里运用了快速转置，降低时间复杂度

2、快速转置的核心是确定转置后矩阵，每行的第一个非零元在三元表中的序号

3、详细在代码注释中文章来源地址https://www.toymoban.com/news/detail-715413.html

代码：

#include<iostream>
using namespace std;
typedef struct node
{
	int i, j, e;
}Triple;
typedef struct node1
{
	node data[1000];
	int mu, nu, tu=0;//矩阵行数、列数、非零元个数
}TSMatrix;
void Transpose(TSMatrix m, TSMatrix& t)
{
	int num[100]={0}, head[100];
	t.mu = m.nu, t.nu = m.mu, t.tu = m.tu;
	if (t.tu)//非零元不为0个，则做下列操作
	{
		for (int i = 1; i <= t.mu; i++)//逆置矩阵的列变行，初始每行中的非零元个数为0
			num[i] = 0;
		for (int i = 1; i <= t.tu; i++)//遍历非零元
			num[m.data[i].j]++;//列变行，m中每列的非零元个数就是t中每列非零元的个数
		head[1] = 1;
		for (int i = 2; i <= t.mu; i++)//遍历t的行数
			head[i] = head[i - 1] + num[i-1];//每行的第一个非零元在三元表中的序号
		for (int i = 1; i <= t.tu; i++)//遍历非零元
		{
			int col = m.data[i].j;//取非零元的列数
			int l = head[col];//该列要存储的位置
			t.data[l].i = m.data[i].j, t.data[l].j = m.data[i].i;//行转列，列转行
			t.data[l].e = m.data[i].e;
			head[col]++;//该列元素下次存储往下一位
		}

	}
}
int main()
{
	TSMatrix m,t;
	int ju[51][51];
	cout << "输入行数，列数：" << endl;
	cin >>m.mu >> m.nu;
	for (int i = 1; i <= m.mu; i++)//输入初始矩阵,建立三元组
		for (int j = 1; j <= m.nu; j++)
		{
			cin >> ju[i][j];
			if (ju[i][j] != 0)
			{
				m.tu++;
				m.data[m.tu].e = ju[i][j];
				m.data[m.tu].i = i, m.data[m.tu].j = j;
			}
		}
	Transpose(m, t);
	//for (int i = 1; i <= m.tu; i++)
		//cout << m.data[i].e << " " << m.data[i].i << " " << m.data[i].j << endl;
	//cout << endl;
	//for (int i = 1; i <= t.tu; i++)
		//cout << t.data[i].e << " " << t.data[i].i << " " << t.data[i].j << endl;
	cout << "逆置后矩阵：" << endl;
	int k = 1;
	for (int i = 1; i <= t.mu; i++)
	{
		for (int j = 1; j <= t.nu; j++)
		{
			if (t.data[k].i == i && t.data[k].j == j)
				cout << t.data[k++].e << " ";
			else
				cout << "0 ";
		}
		cout << endl;
	}

}

到了这里，关于三元组（C++ 实现矩阵快速转置)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！