链式二叉树的实现
1.了解三种遍历方式
学习链式二叉树要知道三种遍历方式,便于对二叉树的节点以及左子树和右子树进行操作。
前序遍历:根、左子树、右子树
中序遍历:左子树、根、右子树
后序遍历:左子树、右子树、根
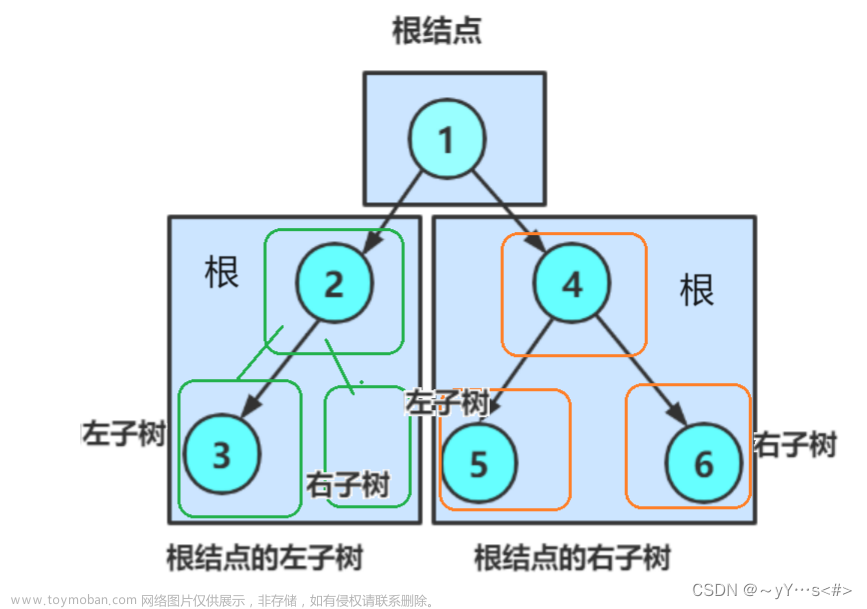
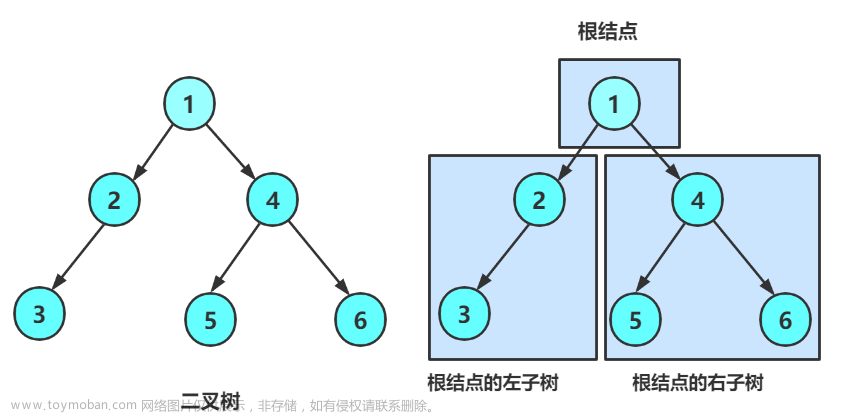
以下图为例:
得到的结果:
前序遍历:1 2 3 4 5 6
中序遍历:3 2 1 5 4 6
后序遍历:3 2 5 6 4 1
2.构建二叉树
构建二叉树有两种方式,一种是手动构建,另一种是前序遍历构建
(1)手动构建
创建需要的节点,然后把它们按照自己想要的结构连接起来即可
BTNode* CreatBinaryTree()
{
BTNode* node1 = BuyNode(1);
BTNode* node2 = BuyNode(2);
BTNode* node3 = BuyNode(3);
BTNode* node4 = BuyNode(4);
BTNode* node5 = BuyNode(5);
BTNode* node6 = BuyNode(6);
node1->left = node2;
node1->right = node4;
node2->left = node3;
node4->left = node5;
node4->right = node6;
return node1;
}
(2)前序遍历构建
首先函数参数传过来一个数组,数组可以是数字也可以是字符,这里用字符数组进行演示。
char arr[] = “ABD##E#H##CF##G##”;// # 代表空
我们还需要一个变量 i 来记录数组下标的位置,i 初始化为0。
注意:传变量 i 的时候要传它的地址,因为等会函数递归 i 的值也要改变,改变函数参数的值要有它的地址才行。
进入函数,首先判断当前 i 下标指向的位置是不是 # ,如果是,返回空指针,i 位置往后走;不是,开辟空间创建一个节点(记得判空),把当前位置的字符赋给节点的值,i 位置往后走。
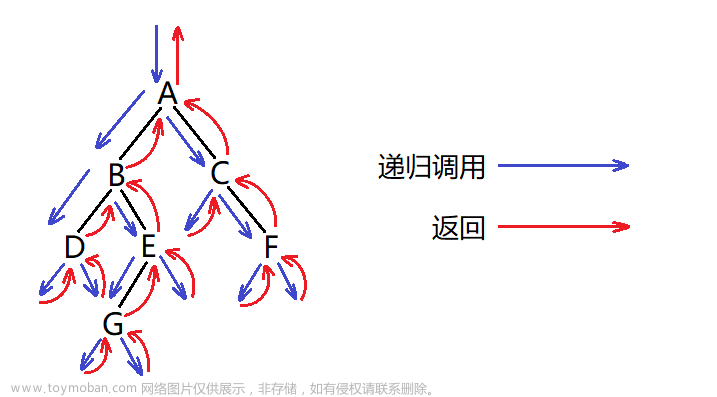
以上是前序遍历的根左右中的根部分,即当前节点创建完毕,接着要连接它的孩子节点。用函数递归的方式使当前节点进入它的孩子节点,孩子节点可以返回(连接)上一层节点。最后返回根节点。
树的形状:
BTNode* TreeCreate(char* a, int* pi)
{
//如果是 # 说明为空返回上一层函数
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//不是空,开辟一个节点大小的空间,创建一个节点
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
//赋值
root->val = a[*pi];
(*pi)++;
//当前节点连接孩子节点
root->left = TreeCreate(a, pi);
root->right = TreeCreate(a, pi);
//当前节点连接上一个节点 || 返回根节点
return root;
}
3.二叉树的销毁
销毁二叉树从叶子节点开始销毁,采用后续遍历的思路。递归到树的最下层,也就是叶子节点,当递归到空指针时返回上一层函数,当前节点的左子树和右子树都递归好了,就销毁当前节点,然后返回上一层函数,以此类推。
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
}
4.二叉树节点个数
当前节点如果是空指针,返回0;不是空指针,先进入它的左函数(左子树),在左函数中还是先判断是否为空指针,是,返回0,不是,接着还是先进入它的左函数,如果次时它的左函数的这个节点为空,就返回0,然后进入它的右函数,也是空,返回0。当前节点的左右都是空但这个节点不为空,返回1,到上一层函数,以此类推,每返回一个节点加1
int TreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
5.二叉树叶子节点个数
叶子节点的特点是它的左右子树都为空指针,还是用递归的思路,当节点递归到空指针,返回0;如果当前节点的左右子树都满足为空指针,说明当前节点是叶子节点,返回1
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
else
{
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
}
6.二叉树第k层节点个数
传进一个参数k,k的值就是二叉树的某一层(根节点为第一层)。当k等于1时,在第一层;k等于2时,在第二层;k等于3时,在第三层……可以使用一个方法,当k等于1时,就是在第k层,用函数递归,每递归到下一层,k的值减1,直到k等于1;当前节点k为1时,就返回1,最后可以统计出第k层的节点个数。
int TreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}
7.二叉树查找值为x的节点
查找值为x的节点,找到则返回这个节点,否则返回空。当前节点如果是空指针,返回空到上一层函数。如果当前节点不为空,判断这个节点的值是否是x,如果是,返回这个节点到上一层函数;不是,创建一个变量,让这个变量接收递归的下一个函数的返回值,然后下面判断这个变量是否为空,是空进入另一个函数递归,不是返回这个变量到上一层函数(这个变量就是找到的节点)。如果没有要找的节点,返回空。
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
BTNode* ret = NULL;
ret = TreeFind(root->left, x);
if (ret)
{
return ret;
}
ret = TreeFind(root->right, x);
if (ret)
{
return ret;
}
return NULL;
}
8.二叉树的前、中、后序遍历
根据二叉树的三种遍历方式打印节点,每种方式的打印顺序不同。
//二叉树前序遍历
void TreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%c ", root->val);
TreePrevOrder(root->left);
TreePrevOrder(root->right);
}
//二叉树中序遍历
void TreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeInOrder(root->left);
printf("%c ", root->val);
TreeInOrder(root->right);
}
//二叉树后序遍历
void TreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
TreePostOrder(root->left);
TreePostOrder(root->right);
printf("%c ", root->val);
}
9.二叉树的层序遍历
层序遍历是一层一层的打印节点数据,需要用队列,队列的特点是先进先出。我们可以先往队列里放入根节点,此时队列不为空,然后用一个临时变量获取队列的头元素(此时就是根节点),判断它的左孩子是不是空,不是空,往队列放入左孩子节点,是空就跳过;右孩子同理。接着打印这个临时变量节点的值,再把从队列里删除掉。因为前面有放入节点,所以队列不为空,就继续前面的步骤,这样就可以一层一层的打印每个节点的值,直到队列为空跳出结束。
void TreeLevelOrder(BTNode* root)
{
Que q;
QueInit(&q);
QuePush(&q, root);
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front->left)
{
QuePush(&q, front->left);
}
if (front->right)
{
QuePush(&q, front->right);
}
printf("%c ", front->val);
QuePop(&q);
}
}
10.判断二叉树是否是完全二叉树
判断是不是完全二叉树还是用队列的结构,队列可以层序遍历,一层一层的进入数据。完全二叉树的特点是前h-1层是满的,最后一层可能是满的,也可能是不满的,并且它的最后一层必须从左到右是连续的。
这里要有两个循环控制,第一个循环里层序往队列中放入节点(包括空),定义一个临时变量获取队列的头元素,判断它是不是空,是空,就跳出第一个循环,到第二个循环;不是空,往队列放入它的左右孩子节点(空也放入)。
到第二个循环,如果这个二叉树是完全二叉树,就不会进入第二个循环,因为是完全二叉树的话,在第一个循环它遇到空才跳出,此时这个空的后面就没有节点了,到第二个循环时,由于空后面没有节点,所以队列已经是空的,不会进入第二个循环,直接返回0,是完全二叉树。
如果这个二叉树不是完全二叉树,那么在第一个循环遇到空跳出后,它的后面还有节点,此时队列不为空,继续用前面的方法,定义一个临时变量获取队列头元素,判断是不是空,是空,删除这个空,继续判断(不管空与节点之间隔多少,它们都在队列里,因此队列不为空继续判断、删除,直到队列为空才停下);不是空,说明还有节点,直接返回1,不是完全二叉树。文章来源:https://www.toymoban.com/news/detail-715781.html
int TreeComplete(BTNode* root)
{
Que q;
QueInit(&q);
QuePush(&q, root);
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front == NULL)
{
break;
}
QuePush(&q, front->left);
QuePush(&q, front->right);
QuePop(&q);
}
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front != NULL)
{
return 1;
}
QuePop(&q);
}
return 0;
}
全部代码
1.BinaryTree.h
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>
#include <string.h>
#include <stdbool.h>
typedef char BTDataType;
typedef struct BinaryTreeNode
{
BTDataType val;
struct BinaryTreeNode* left;
struct BinaryTreeNode* right;
}BTNode;
typedef BTNode* QDataType;
typedef struct QueueNode
{
QDataType data;
struct QueueNode* next;
}QNode;
typedef struct Queue
{
QNode* head;
QNode* tail;
int size;
}Que;
//构建二叉树
BTNode* TreeCreate(char* a, int* pi);
//二叉树销毁
void TreeDestroy(BTNode* root);
//二叉树节点个数
int TreeSize(BTNode* root);
//二叉树叶子节点个数
int TreeLeafSize(BTNode* root);
//二叉树第k层节点个数
int TreeLevelKSize(BTNode* root, int k);
//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x);
//二叉树前序遍历
void TreePrevOrder(BTNode* root);
//二叉树中序遍历
void TreeInOrder(BTNode* root);
//二叉树后序遍历
void TreePostOrder(BTNode* root);
//层序遍历
void TreeLevelOrder(BTNode* root);
//判断二叉树是否是完全二叉树
int TreeComplete(BTNode* root);
//初始化
void QueInit(Que* pq);
//销毁
void QueDestroy(Que* pq);
//入队
void QuePush(Que* pq, QDataType x);
//出队
void QuePop(Que* pq);
//获取头部元素
QDataType QueFront(Que* pq);
//获取队尾元素
QDataType QueBack(Que* pq);
//获取元素个数
int QueSize(Que* pq);
//检查是否为空
bool QueEmpty(Que* pq);
2.BinaryTree.c
#include "BinaryTree.h"
//构建二叉树
BTNode* TreeCreate(char* a, int* pi)
{
//如果是 # 说明为空返回上一层函数
if (a[*pi] == '#')
{
(*pi)++;
return NULL;
}
//不是空,开辟一个节点大小的空间,创建一个节点
BTNode* root = (BTNode*)malloc(sizeof(BTNode));
if (root == NULL)
{
perror("malloc fail");
exit(-1);
}
root->val = a[*pi];
(*pi)++;
//当前节点连接孩子节点
root->left = TreeCreate(a, pi);
root->right = TreeCreate(a, pi);
//当前节点连接上一个节点 || 返回根节点
return root;
}
//二叉树销毁
void TreeDestroy(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
}
//二叉树节点个数
int TreeSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
return TreeSize(root->left) + TreeSize(root->right) + 1;
}
//二叉树叶子节点个数
int TreeLeafSize(BTNode* root)
{
if (root == NULL)
{
return 0;
}
if (root->left == NULL && root->right == NULL)
{
return 1;
}
else
{
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
}
//二叉树第k层节点个数
int TreeLevelKSize(BTNode* root, int k)
{
if (root == NULL)
{
return 0;
}
if (k == 1)
{
return 1;
}
return TreeLevelKSize(root->left, k - 1) + TreeLevelKSize(root->right, k - 1);
}
//二叉树查找值为x的节点
BTNode* TreeFind(BTNode* root, BTDataType x)
{
if (root == NULL)
{
return NULL;
}
if (root->val == x)
{
return root;
}
BTNode* ret = NULL;
ret = TreeFind(root->left, x);
if (ret)
{
return ret;
}
ret = TreeFind(root->right, x);
if (ret)
{
return ret;
}
return NULL;
}
//二叉树前序遍历
void TreePrevOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
printf("%c ", root->val);
TreePrevOrder(root->left);
TreePrevOrder(root->right);
}
//二叉树中序遍历
void TreeInOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
TreeInOrder(root->left);
printf("%c ", root->val);
TreeInOrder(root->right);
}
//二叉树后序遍历
void TreePostOrder(BTNode* root)
{
if (root == NULL)
{
return;
}
TreePostOrder(root->left);
TreePostOrder(root->right);
printf("%c ", root->val);
}
//层序遍历
void TreeLevelOrder(BTNode* root)
{
Que q;
QueInit(&q);
QuePush(&q, root);
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front->left)
{
QuePush(&q, front->left);
}
if (front->right)
{
QuePush(&q, front->right);
}
printf("%c ", front->val);
QuePop(&q);
}
}
//判断二叉树是否是完全二叉树
int TreeComplete(BTNode* root)
{
Que q;
QueInit(&q);
QuePush(&q, root);
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front == NULL)
{
break;
}
QuePush(&q, front->left);
QuePush(&q, front->right);
QuePop(&q);
}
while (!QueEmpty(&q))
{
BTNode* front = QueFront(&q);
if (front != NULL)
{
return 1;
}
QuePop(&q);
}
return 0;
}
//初始化
void QueInit(Que* pq)
{
assert(pq);
pq->head = NULL;
pq->tail = NULL;
pq->size = 0;
}
//销毁
void QueDestroy(Que* pq)
{
assert(pq);
QNode* cur = pq->head;
while (cur)
{
QNode* next = cur->next;
free(cur);
cur = next;
}
pq->head = pq->tail = NULL;
pq->size = 0;
}
//入队
void QuePush(Que* pq, QDataType x)
{
assert(pq);
QNode* newnode = (QNode*)malloc(sizeof(QNode));
if (newnode == NULL)
{
perror("malloc fail");
exit(-1);
}
newnode->data = x;
newnode->next = NULL;
if (pq->tail == NULL)
{
pq->head = pq->tail = newnode;
}
else
{
pq->tail->next = newnode;
pq->tail = newnode;
}
pq->size++;
}
//出队
void QuePop(Que* pq)
{
assert(pq);
assert(!QueEmpty(pq));
if (pq->head->next == NULL)
{
free(pq->head);
pq->head = pq->tail = NULL;
}
else
{
QNode* next = pq->head->next;
free(pq->head);
pq->head = next;
}
pq->size--;
}
//获取头部元素
QDataType QueFront(Que* pq)
{
assert(pq);
assert(!QueEmpty(pq));
return pq->head->data;
}
//获取队尾元素
QDataType QueBack(Que* pq)
{
assert(pq);
assert(!QueEmpty(pq));
return pq->tail->data;
}
//获取元素个数
int QueSize(Que* pq)
{
assert(pq);
return pq->size;
}
//检查是否为空
bool QueEmpty(Que* pq)
{
assert(pq);
return pq->head == NULL;
}
3.test.c
#include "BinaryTree.h"
int main()
{
char arr[] = "ABD##E#H##CF##G##";
int i = 0;
//构建二叉树
BTNode* root = TreeCreate(arr, &i);
//二叉树节点个数
printf("二叉树节点个数:");
printf("%d ", TreeSize(root));
printf("\n");
//二叉树叶子节点个数
printf("二叉树叶子节点个数:");
printf("%d ", TreeLeafSize(root));
printf("\n");
//二叉树第k层节点个数
printf("二叉树第k层节点个数:");
int k = 3;
printf("%d ", TreeLevelKSize(root, k));
printf("\n");
//二叉树查找值为x的节点
char x = 'G';
BTNode* rec = TreeFind(root, x);
if (rec)
{
printf("找到了\n");
}
else
{
printf("没找到\n");
}
//二叉树前序遍历
printf("前:");
TreePrevOrder(root);
printf("\n");
//二叉树中序遍历
printf("中:");
TreeInOrder(root);
printf("\n");
//二叉树后序遍历
printf("后:");
TreePostOrder(root);
printf("\n");
//层序遍历
printf("层序:");
TreeLevelOrder(root);
printf("\n");
//判断二叉树是否是完全二叉树
if (0 == TreeComplete(root))
{
printf("是完全二叉树\n");
}
else
printf("不是完全二叉树\n");
//二叉树销毁
TreeDestroy(root);
return 0;
}

感谢观看~文章来源地址https://www.toymoban.com/news/detail-715781.html
到了这里,关于【数据结构】二叉树的链式结构的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!