1. Toy模板网首页
  2. > Toy博客

矩阵计算器

10月前 作者：y1837095621 分类：Toy博客 阅读(45) 违法举报

这篇具有很好参考价值的文章主要介绍了矩阵计算器。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

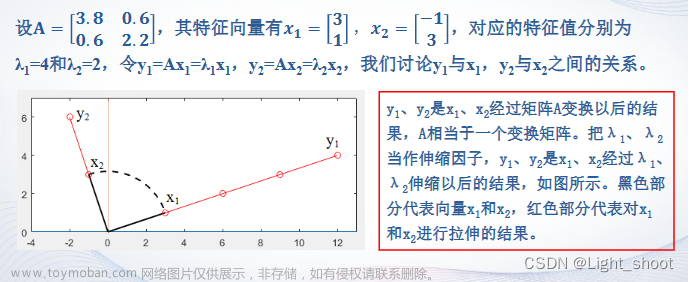
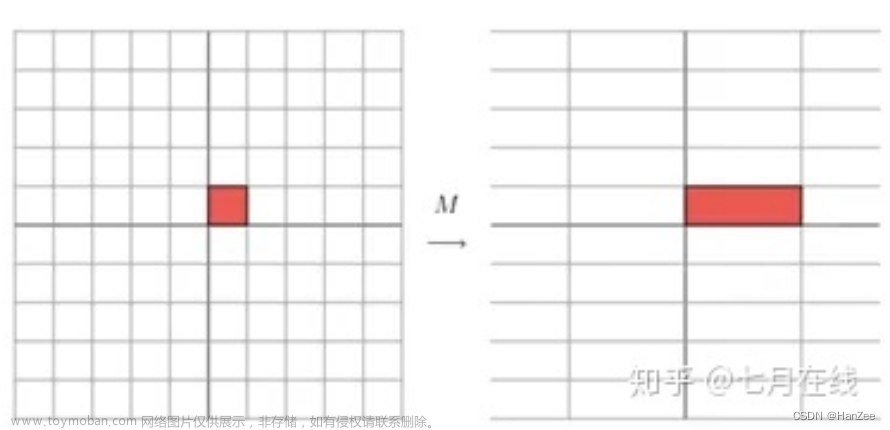
摘要：在本报告中介绍了一套图形界面的矩阵计算器的的想法与需求分析、设计、实现，测试和改进。在想法与需求分析中介绍了我研发此程序的契机和原因。在设计中介绍了对该程序的设计，以及如何实现。实现中介绍了对关键代码的分析和解释。测试以图片的形式证明了一些具体功能的实现和验证。最后的改进中介绍了程序的还存在的漏洞与需要改进的地方。

关键字：矩阵；计算；图形化；方便

  1. 想法与需求分析
    1. 想法

作为一名工科专业大学生，我们会在读大学的途中遇到《线性代数》这样一门课程。这门课程主要讲了与矩阵相关的计算与分析。但是在学习过程中，我们会遇到一些比较复杂的矩阵的运算，如求矩阵的逆，求矩阵的行列式的值，求矩阵的特征值，等。对于刚刚接触这门课程的大学生来说十分的困难，有时候疯狂的计算了很长时间都不能得到正确的结果，让人的心态十分的炸裂，很容易让我们脆弱的心灵受到伤害，于是我设计了这款矩阵计算器。

    1. 需求分析

当前比较常见的计算器，对矩阵的计算操作十分的复杂，首先要定义矩阵，然后再定义的矩阵中选取几个进行运算，矩阵最大只有4*4，最多也只能存储4个，功能也不全面。而且还要仔细的阅读说明书才能正确的操作，十分的复杂。手机上自带的计算器也没有计算矩阵的功能。而更高级的计算器又需要花费很多的钱。而我利用python编写了一款带有图形界面的矩阵计算器，可以实现对于矩阵的一些基本的运算与操作。对于大学生学习《线性代数》有很大的帮助，在它的帮助下学习效率会得到提高。不仅提高了计算的效率，同时也能验证手算结果是否正确。

  1. 设计
    1. 布局

特征值计算器,python
首先对计算器的整体构造进行排版和布局，仿照传统计算器的样式，利用pyqt5,先在界面的上半部分设计一个多行的可编辑文本框plainTextEdit。之后在下方利用layout进行排版创建一个5*5的按钮组，按钮组中的25个按钮分别为：空格，行列式的值，转置矩阵，特征值与向量，清空，删除，逆矩阵，0，高斯消元法。换行，7,8,9，+，-，4,5,6，X，.，1,2,3，Ans，=。通过按钮点击相应事件用来实现计算器不同的功能。效果如图：

    1. 功能

本矩阵计算器通过点击按钮实现矩阵的输入，加减乘计算，逆矩阵，转置矩阵，求特征值与特征向量，求行列式的值，通过增广矩阵的高斯消元法求一些方程的解。

点击数字或者符号，会直接在多行文本编辑框内出现相应的数字或者符号。输入每个数据需要用空格隔开，点击换行会输出下一行的数据。

当输入一个矩阵后，若点击逆矩阵，转置矩阵等操作时，在输入矩阵满足前提条件情况下会直接将结果输出在多行文本编辑框内，并将结果存入Ans中。若点击等于号，则会把该矩阵存入Ans中。若点击运算符号则会自动换行，输入下一个矩阵。当第二个矩阵输入完成后，点击等于号，在输入矩阵满足前提条件情况下会直接将结果输出在多行文本编辑框内，并将结果存入Ans中。

点击Ans,后点击等于号，会将Ans存储的结果输出。而且上述对于矩阵的操作对Ans也同样生效，对于矩阵的运算也可以结合Ans进行。

  1. 实现
    1. 点击数字按钮
# 点击1

def clickbutton1(self=None):

    global bo

    if bo == 0:

        self.plainTextEdit.insertPlainText("1")

    else:

        bo = 0

        self.plainTextEdit.appendPlainText("1")

分析：

以数字1为例。bo为全局变量，主要用来判断当前是否处于换行状态，处于换行状态使用函数iappendPlainText会使数字输出在新的一段，若不处于换行状态则使用insertPlainText函数直接在本段追加。

    1. 点击符号按钮
  2. def clickbuttonadd(self=None):     self.plainTextEdit.appendPlainText("+")     global bo     bo = 1

分析：

以加号为例。对运算更加方便的操作，点击符号按钮后直接另起一段进行输入，并将换行标志bo置为1，下一次的输入也是另起一段，方便矩阵的输入。

3.3点击操作按钮

# 点击清空

def clickbuttonclear(self=None):

    self.plainTextEdit.clear()



# 点击换行

def clickbutton_huanhang(self=None):

    global bo

    bo = 1

# 点击删除

def clickbuttondelete(self=None):

    text_cursor = QTextCursor(self.plainTextEdit.document())

    text_cursor.movePosition(QTextCursor.End)

    text_cursor.deletePreviousChar()

特征值计算器,python

分析：

点击清空会用clear函数将文本框清空，点击换行会让换行标志bo为1，使下一次输入另起一段，而点击删除按钮则是使用QTextCursor选择文本编辑框中的内容并将光标移动到最后一个字符处，使用deletPreviousChar函数直接将前一个字符删除。

3.4点击逆矩阵按钮

def clickbuttoninverse(self=None):

    st = self.plainTextEdit.toPlainText()

    x = len(st.split('\n'))

    y = len((st.split('\n')[0]).split())

    global ans

    if x != y:

        self.plainTextEdit.setPlainText("错误")

    else:

        if st == "Ans":

            num = ans

        else:

            num = np.ones((x, y))

            for i in range(x):

                for j in range(y):

                    num[i][j] = (st.split('\n')[i]).split()[j]

            p = np.linalg.det(num)

            if p == 0:

                self.plainTextEdit.setPlainText("错误")

        num = np.linalg.inv(num)

        ans = num

        self.plainTextEdit.clear()

        for i in range(x):

            for j in range(y):

                if j == 0:

                    self.plainTextEdit.appendPlainText(str(num[i][j]))

                    self.plainTextEdit.insertPlainText(" ")

                else:

                    self.plainTextEdit.insertPlainText(str(num[i][j]))

                    self.plainTextEdit.insertPlainText(" ")

特征值计算器,python

分析：

首先点击该按钮时，文本编辑框内已经有了一个完整的矩阵或是Ans。之后将文本框内的数据读取为字符串。之后通过split()对字符串进行操作，先以换行符进行分割，可以求出当前矩阵的行数，之后选取一行以空格进行分割，可以求出当前矩阵的列数。之后通过求得的行数与列数创建一个全1矩阵num。矩阵num的每个元素与字符串中的位置一一对应。通过分割字符串。循环赋值构建矩阵，并求其行列式，因为行列式为0的矩阵没有逆矩阵因此输出错误。若行列式不为0，利用np.linalg.inv函数计算逆矩阵。按矩阵顺序输出结果到文本编辑框内，并将结果存入Ans中。

若文本编辑框内本来便是Ans,则直接进行运算，省去提取矩阵的步骤。

3.5点击行列式的值按钮

# 点击行列式的值

def clickbuttondeterminant(self=None):

    st = self.plainTextEdit.toPlainText()

    x = len(st.split('\n'))

    y = len((st.split('\n')[0]).split())

    global ans

    if x != y:

        self.plainTextEdit.setPlainText("错误")

    else:

        if st == "Ans":

            num = ans

        else:

            num = np.ones((x, y))

            for i in range(x):

                for j in range(y):

                    num[i][j] = (st.split('\n')[i]).split()[j]

        p = np.linalg.det(num)

        p = round(p, 7)

        ans = p

        self.plainTextEdit.setPlainText(str(p))

特征值计算器,python

分析：

点击该按钮时，会有与逆矩阵相似的方法提取当前文本编辑框中的矩阵，之后利用np.linalg.det函数 计算行列式的值，因为矩阵转化之后所有数据均为浮点数，而浮点数会在计算的过程中产生不可避免的精度误差，于是我采用了保留小数的方法消除误差，并将结果存入Ans中。

3.6点击转置矩阵按钮

# 点击转置矩阵

def clickbuttontransposition(self=None):

    st = self.plainTextEdit.toPlainText()

    x = len(st.split('\n'))

    y = len((st.split('\n')[0]).split())

    global ans

    if st == "Ans":

        num = ans

    else:

        num = np.ones((x, y))

        for i in range(x):

            for j in range(y):

                num[i][j] = (st.split('\n')[i]).split()[j]

    num = num.transpose()

    ans = num

    self.plainTextEdit.clear()

    self.plainTextEdit.setPlainText(str(num))

特征值计算器,python

分析：

   点击转置矩阵的按钮后，会用类似逆矩阵的方法求得当前矩阵，利用.transpose函数求得转置矩阵并输出，结果保留在Ans中。

3.7点击特征值与特征向量按钮

# 点击特征值与特征向量

def clickbuttoneigenvalues(self=None):

    st = self.plainTextEdit.toPlainText()

    x = len(st.split('\n'))

    y = len((st.split('\n')[0]).split())

    if x != y:

        self.plainTextEdit.setPlainText("错误")

    else:

        global ans

        if st == "Ans":

            num = ans

        else:

            num = np.ones((x, y))

            for i in range(x):

                for j in range(y):

                    num[i][j] = (st.split('\n')[i]).split()[j]

        eigenvalues, eigenvectors = np.linalg.eig(num)

        self.plainTextEdit.clear()

        self.plainTextEdit.appendPlainText(str(eigenvalues))

        self.plainTextEdit.appendPlainText(str(eigenvectors))

特征值计算器,python

分析：

由于设计时出现了26个按钮，无法漂亮的排版，于是只能将求特征值与特征向量合并到一起，只是无法将两个结果赋值到Ans中。

点击特征值与特征向量的按钮后，会用类似逆矩阵的方法求得当前矩阵，利用np.linalg.eig函数求得转置矩阵并输出。

3.8点击高斯消元法按钮

def clickbuttongaosi(self=None):

    st = self.plainTextEdit.toPlainText()

    x = len(st.split('\n'))

    y = len((st.split('\n')[0]).split())

    num = np.ones((x, y))

    res = np.ones((x, y - 1))

    for i in range(x):

        for j in range(y):

            num[i][j] = (st.split('\n')[i]).split()[j]

    for i in range(x):

        for j in range(y - 1):

            res[i][j] = num[i][j]

    if np.linalg.matrix_rank(res) < np.linalg.matrix_rank(num):

        self.plainTextEdit.setPlainText("有无数解")

    if np.linalg.matrix_rank(res) > np.linalg.matrix_rank(num):

        self.plainTextEdit.setPlainText("无解")

    if np.linalg.matrix_rank(res) == np.linalg.matrix_rank(num):

        self.plainTextEdit.clear()

        for i in range(x - 1):

            for j in range(i + 1, x):

                temp = num[j][i] / num[i][i]

                for t in range(i, y):

                    num[j][t] = num[j][t] - temp * num[i][t]

        for i in range(np.linalg.matrix_rank(num) - 1, -1, -1):

            res[i][1] = num[i][y - 1]

            for j in range(i + 1, np.linalg.matrix_rank(num)):

                res[i][1] = res[i][1] - num[i][j] * res[j][0]

            res[i][0] = res[i][1] / num[i][i]

        for i in range(np.linalg.matrix_rank(num)):

            res[i][0] = round(res[i][0], 7)

            self.plainTextEdit.appendPlainText(str(res[i][0]))

特征值计算器,python

分析：

首先使用了类似于求逆矩阵中将字符串转化为矩阵的方法。得到矩阵num。之后删去矩阵的最后一列，得到了系数矩阵res。利用np.linalg.matrix_rank函数分别求出系数矩阵与增广矩阵的秩。

当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均等于方程组中未知数个数n的时候，方程组有唯一解。

当方程组的系数矩阵的秩与方程组增广矩阵的秩相等且均小于方程组中未知数个数n的时候，方程组有无穷多解。

当方程组的系数矩阵的秩小于方程组增广矩阵的秩的时候，方程组无解。

当确定方程组有唯一解后，利用循环，将每一行的第一个非0的数转化为0，得到一个上三角矩阵。之后利用系数矩阵的第一列存储方程的解，第二列存储计算过程中的中间值，倒序求取方程的解并将结果输出。

3.9点击等号按钮

# 点击等于号

def clickbuttequal(self=None):

    st = self.plainTextEdit.toPlainText()

    global ans

    temp = 1

    x = len(st.split('\n'))

    if st == "Ans":

        self.plainTextEdit.setPlainText(str(ans))

    else:

        for i in range(x):

            if st.split('\n')[i] == "Ans" and i == x - 1:

                temp = 0

                x1 = x - 2

                y1 = len((st.split('\n')[0]).split())

                op = st.split('\n')[x - 2]

                num2 = ans

                x2 = ans.shape[0]

                y2 = ans.shape[1]

                num1 = np.ones((x1, y1))

                for t in range(x1):

                    for j in range(y1):

                        num1[t][j] = (st.split('\n')[t]).split()[j]

                break

            if st.split('\n')[i] == "Ans" and i == 0:

                temp = 0

                x2 = x - 2

                y2 = len((st.split('\n')[x2]).split())

                num1 = ans

                op = st.split('\n')[1]

                x1 = ans.shape[0]

                y1 = ans.shape[1]

                num2 = np.ones((x2, y2))

                for t in range(2, x):

                    for j in range(y2):

                        num2[t -2][j] = (st.split('\n')[t]).split()[j]

                break

        if temp:

            x1 = 0

            for i in range(x):

                if (st.split('\n')[i]).split()[0] == 'X' or (st.split('\n')[i]).split()[0] == '+' or \

                        (st.split('\n')[i]).split()[0] == '-':

                    op = (st.split('\n')[i]).split()[0]

                    x1 = i

                    break

            if x1 == 0:

                y = len((st.split('\n')[0]).split())

                num = np.ones((x, y))

                for i in range(x):

                    for j in range(y):

                        num[i][j] = (st.split('\n')[i]).split()[j]

                ans = num

                self.plainTextEdit.setPlainText(str(ans))

            else:

                y1 = len((st.split('\n')[0]).split())

                y2 = len((st.split('\n')[x1 + 1]).split())

                x2 = x - x1 - 1

                print(x1, y1, x2, y2)

                num1 = np.ones((x1, y1))

                num2 = np.ones((x2, y2))

                for i in range(x1):

                    for j in range(y1):

                        num1[i][j] = (st.split('\n')[i]).split()[j]

                for i in range(x1 + 1, x):

                    for j in range(y2):

                        num2[i - 1 - x1][j] = (st.split('\n')[i]).split()[j]

        if x1 != 0:

            if op == '+':

                if x1 == x2 and y1 == y2:

                    ans = num1 + num2

                    self.plainTextEdit.setPlainText(str(ans))

                else:

                    self.plainTextEdit.setPlainText("错误")

            if op == '-':

                if x1 == x2 and y1 == y2:

                    ans = num1 - num2

                    self.plainTextEdit.setPlainText(str(ans))

                else:

                    self.plainTextEdit.setPlainText("错误")

            if op == 'X':

                if y1 == x2:

                    ans = np.dot(num1, num2)

                    self.plainTextEdit.setPlainText(str(ans))

                else:

                    self.plainTextEdit.setPlainText("错误")

特征值计算器,python

分析：

点击等于号后需要分情况讨论。

当点击等于号后检测到文本输入框内只有一个矩阵时，将矩阵存入Ans中并输出。

   当点击等于号后检测到文本输入框内只有Ans时，直接将Ans的内容输出。

   当点击等于号后检测到文本输入框内有两个矩阵和运算符时，首先将文本框中的内容全部转化为字符串，以换行符为分割符进行分割，求出当前总行数。

之后进行循环，检测每一行是否为Ans，若存在Ans，记录其出现的位置。

若出现在第一行。则将其赋值给运算矩阵num1,记录其行数和列数，运算符便位于第二行，将运算符记录。然后使用经典方法将运算符之后字符串的分割赋值转化为计算矩阵num2。

若出现在最后一行。则将其赋值给运算矩阵num2,记录其行数和列数，运算符便位于倒数二行，将运算符记录。然后使用经典方法将运算符之后字符串的分割赋值转化为计算矩阵num1。

若不存在Ans，则需要寻找运算符的位置找到之后，记录运算符。将运算符之前的字符串使用经典方法分割赋值给运算矩阵num1,将运算符之后的字符串使用经典方法分割赋值给运算矩阵num2。

之后进入计算的判断，首先判断运算符。

若为加或减，则判断两个运算矩阵行和列是否相等，不满足输出错误，满足进行运算，并把结果存入Ans中。

若为乘，则判断第一个矩阵列是否等于第二个矩阵的行，不满足输出错误，满足进行运算，并把结果存入Ans中。

4.测试

4.1逆矩阵

样例输入：

（1）1 2

2 1

（2）1 1 1

     2 3 4

     4 5 6


  

特征值计算器,python特征值计算器,python

4.2转置矩阵

样例输入：

    1. 2

     3 4

（2）1 2

     4 5

     8 9 


样例输出：

特征值计算器,python

特征值计算器,python

4.3行列式的值

样例输入：

（1）1 2

     2 1

（2）1.2 2 1

     4.5 4 3

     8.2 1 2


样例输出：

特征值计算器,python

 特征值计算器,python

4.4特征值与特征向量

样例输入：

（1）1 2

     2 1


样例输出：

特征值计算器,python

4.5等号计算

样例输入：

（1）1 2

     2 1

  +

  4 4

  7 8

（2）Ans(此时Ans为上一次（1）运算的结果)

     -

     2 7

     1 1

（3）1 2 3

     4 5 6

     X

     Ans(此时Ans为上一次（2）运算的结果)


样例输出：

特征值计算器,python

 特征值计算器,python

 特征值计算器,python

  1. 改进

我所编辑的矩阵计算器能基本的解决一些基础的有关的矩阵的简答基本的计算，供学生使用，系统的应用了在Python课堂上学习的pyqt5可视化界面的编辑。对字符串的处理以及分析，对条件语句的熟练使用等等。但是还是有许多的弊端，如对于运算错误的处理，因为在编辑计算器的过程中我只是将我所能想到的计算失败的情况做出了处理，并不能涵盖所有的情况，如使用者输入了一个不标准的矩阵，使用者无法进行2个以上的矩阵的运算。需要后续更系统的将所有的不能正常运算的情况总结起来，专门设立对错检验函数，应该会让bug变得更少。

在让其更严谨之后还可以拓展按钮，进行功能的拓展，如矩阵的对角化，求矩阵的正定矩阵等。或是将其与其他相关科目结合，如可以自动计算《数值计算方法》这门课中解多元方程组的迭代矩阵，并判断其是否收敛。等等。甚至可以将矩阵图形化，根据对应的矩阵中的值汇出相应的函数图像。

  1. 致谢

首先要感谢我的老师，在我没有接触过python的情况下带我由浅入胜，由表及里逐步的学习python，逐步的拓展了我的眼界，提高了我的思维。到最后结课的时候也能独自的完成一个比较复杂的大型程序来实现自己的一些想法。虽然过程比较漫长和困难但给了我极大的收获与进步

同时网络上的一些对于python库的归纳总结让我的研究更加省时省力。文章来源地址https://www.toymoban.com/news/detail-716186.html

到了这里，关于矩阵计算器的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值？不会丢解吗？

    【问题证明】矩阵方程化为特征值方程求得的特征值为什么是全部特征值？不会丢解吗？

    这个问题困扰了我好久，一直感觉如果有其他的特征值没法证伪，不过一直存在思想的层面，没有实际解决，今天突然想到动笔来解决，遂得解，证明如下。 这个证明看似证明过后很直观，但实际上思维走向了牛角尖的时候光靠思考是无法得出令人信服的结论的，唯有实际动

    2024年02月05日
    浏览(59)
  • 《数值分析》-3-特征值与特征矩阵

    《数值分析》-3-特征值与特征矩阵

    搜索技术的很多方面的知识发现都依赖于特征值或奇异值问题，涉及到特征值计算问题。 计算特征值没有直接的方法。 定位特征值的计算方法基于幂迭代的思想，这是求解特征值的一类迭代方法。该思想的一个复杂版本被称为QR算法，是确定典型矩阵所有特征值的一般方法。

    2024年02月08日
    浏览(48)
  • MATLAB矩阵的特征值与特征向量

    MATLAB矩阵的特征值与特征向量

    设A是n阶方阵，如果存在常数λ和n维非零列向量x，使得等式Ax = λx 成立，则称λ为A的特征值，x是对应特征值λ的特征向量。 在MATLAB中，计算矩阵的特征值与特征向量的函数是eig，常用的调用格式有两种： E = eig（A）：求矩阵A的全部特征向量值，构成向量E。 [X，D] = eig（A）：

    2024年02月11日
    浏览(42)
  • 5.1 矩阵的特征值和特征向量

    5.1 矩阵的特征值和特征向量

    学习特征值和特征向量的定义和性质，我会采取以下方法： 1. 学习线性代数基础知识：特征值和特征向量是线性代数中的重要概念，需要先掌握线性代数的基础知识，例如向量、矩阵、行列式、逆矩阵、转置、内积、外积等基本概念。 2. 学习特征值和特征向量的定义：特征

    2024年02月02日
    浏览(54)
  • 矩阵分析：特征值分解

    矩阵分析：特征值分解

    伸缩 一个矩阵其实就是一个线性变换，因为一个矩阵乘以一个向量后得到的向量，其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵： 因为这个矩阵M乘以一个向量(x,y)的结果是： 旋转 除了伸缩变换，也可以进行旋转变换。 上面的矩阵是对称的，所以这个变

    2023年04月24日
    浏览(45)
  • 特征值与相似矩阵

    特征值与相似矩阵

    应用：求幂，对角化，二次型，动力系统等等 通俗 ​ 向量α在矩阵A的线性变换作用下，保持方向不变，进行比例为λ的伸缩。 官方（注意是方阵） 特征方程 ​ （λE-A)α = 0 （α!=0）特征向量不能为0，但是 特征值可以为0或虚数 。方程中λ的次数应与A的 阶数相同 ，否则不是

    2024年02月06日
    浏览(53)

  • 线性代数中矩阵的特征值与特征向量

    作者：禅与计算机程序设计艺术 在线性代数中，如果一个$ntimes n$的方阵$A$满足如下两个条件之一： $A$存在实数特征值，即$exists xneq 0:Ax=kx$,其中$kin mathbb{R}$； $lambda_{max}(A)neq 0$（$lambda_{max}(A)$表示$A$的最大特征值），且$||x_{lambda_{max}(A)}||=sqrt{frac{lambda_{max}(A)}{lambda_{

    2024年02月08日
    浏览(54)
  • 从浅到深研究矩阵的特征值、特征向量

    从浅到深研究矩阵的特征值、特征向量

    本篇特征值、特征向量笔记来源于MIT线性代数课程。 对于方阵而言，现在要找一些特殊的数字，即特征值，和特殊的向量，即特征向量。 给定矩阵A，矩阵A作用在向量上，得到向量Ax（A的作用，作用在一个向量上，这其实就类似于函数，输入向量x，得到向量Ax） 在这些向量

    2024年02月12日
    浏览(48)
  • 线性代数（8）：特征值、特征向量和相似矩阵

    线性代数（8）：特征值、特征向量和相似矩阵

            有矩阵 A 为 n 阶矩阵，Ax = λx （ λ 为一个实数，x为 n 维非零列向量 ），则称 λ 为方阵 A 的特征值， x 为特征向量； 1.2.1 公式         求特征值：使 | A - λE | = 0，其解的 λ 值即为矩阵 A 的特征值；         求特征向量： 使 ( A - λE )x = 0,设 x 为与 A 具有

    2024年02月11日
    浏览(51)
  • 线性代数（五） | 矩阵对角化 特征值 特征向量

    线性代数（五） | 矩阵对角化 特征值 特征向量

    矩阵实际上是一种变换,是一种旋转伸缩变换（方阵） 不是方阵的话还有可能是一种升维和降维的变换 直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili 比如A= ( 1 2 2 1 ) begin{pmatrix}12\\\\21end{pmatrix} ( 1 2 ​ 2 1 ​ ) x= ( 1 2 ) begin{pmatrix}1\\\\2end{pmatrix} ( 1 2 ​ ) 我们给x左乘A实际

    2024年02月04日
    浏览(64)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包