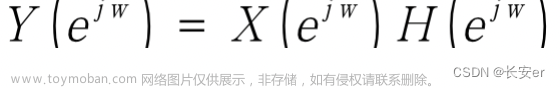对于一个信号来说通常汇入工频噪声往往是因为交流电产生的电泳,影响了我们信号采集导致信号上存在工频干扰。
那么matlab去除工频干扰可以通过陷波滤波器实现。
在python中通常使用scipy.signal实现信号的处理。
Scipy的信号处理模块(scipy.signal)来创建自定义的陷波滤波器。陷波滤波器通常用于去除特定频率上的噪声或干扰,比如电源线干扰。
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 生成示例数据,包括噪声和带有干扰的信号
fs = 1000 # 采样频率
t = np.arange(0, 1, 1/fs)
noise = 0.5 * np.sin(2 * np.pi * 50 * t) # 50 Hz噪声
signal_with_noise = np.sin(2 * np.pi * 5 * t) + noise # 5 Hz信号 + 50 Hz噪声
# 设计陷波滤波器来去除50 Hz干扰
f0 = 50.0 # 噪声的中心频率
Q = 30.0 # 带宽
b, a = signal.iirnotch(f0, Q, fs)
# 使用滤波器来去除噪声
filtered_signal = signal.lfilter(b, a, signal_with_noise)
# 绘制原始信号和去噪后的信号
plt.figure()
plt.subplot(2, 1, 1)
plt.plot(t, signal_with_noise, 'b', label='带噪声的信号')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal, 'g', label='去噪后的信号')
plt.legend()
plt.tight_layout()
plt.show()
上述示例中,signal.iirnotch函数用于设计陷波滤波器的系数,然后使用signal.lfilter来应用该滤波器。这可以帮助去除信号中指定频率的噪声或干扰。
上图中蓝色的线条是,5Hz正弦波,和50Hz干扰正弦波的求和。
绿色的线,是我们规定去irrnotch函数中心频率为50Hz,带宽Q为30进行处理。
实际上说,原始信号有一个正弦信号5Hz。
但是为什么滤波之后原始信号不是光滑的呢?
需要考虑陷波滤波器中心频率的带宽。
在陷波滤波器中,带宽Q(Quality Factor)表示滤波器的调制深度或选择性。它是一个无单位的参数,通常用于定义陷波滤波器的性能。
带宽Q的值越大,滤波器的选择性越高,也就是滤除特定频率附近的信号时,对该频率的抑制会更强。带宽Q的值越小,滤波器的选择性越低,也就是滤除特定频率附近的信号时,对该频率的抑制会较弱。
具体来说,对于陷波滤波器,Q的计算公式通常如下:
Q = f0 / Δf
Q是带宽Q。
f0是你希望去除的频率的中心点。
Δf是带宽,表示你希望保留的频率范围。
Q的值越大,带宽越小,滤波器越窄,抑制特定频率的效果越强。Q的值越小,带宽越大,滤波器越宽,抑制效果越弱。选择Q值的大小通常取决于你的应用和数据中噪声或干扰的性质。常见的Q值范围通常在10到100之间。
在陷波滤波器设计中,选择适当的Q值对于有效地去除特定频率的干扰非常重要。你需要根据具体的应用和数据特点来调整Q值,以获得最佳的滤波效果。




通过对比四个不同的带宽q=1,10,50,100。我们可以观察波形得到结果。
当q=1的时候最接近原始期望得到的5Hz正弦波。但是产生了导数超调,在开始的位置有一个小翘起,那说明就是并不是理想的滤波器。或者说很难得到理想的滤波效果。信号的起始端和结束端都会产生该结果。
在信号处理中,滤波操作可能会引入一些边界效应,特别是在信号的开始和结束段,这种现象通常被称为"边界效应"或"边界伪像"。这是由于滤波器的有限长度以及信号的截断所引起的。
那为什么滤波结束开始端会产生波动,但是信号的结尾段不会产生波动?
边界效应的主要原因包括以下几点:
信号截断:通常,你对一个连续的信号进行离散采样,然后在有限长度的窗口内进行滤波。这会导致信号在开始和结束时被截断,因此,信号在这些边界处可能不连续。
**滤波器的有限长度:**滤波器通常是有限长度的,而不是无限长度。这意味着滤波器本身在时间或频率上也存在截断。当你将有限长度的滤波器应用于信号时,它会影响信号的边界处,引入额外的波动。
**初始条件和阶跃响应:**在滤波器的应用过程中,初始条件和滤波器的阶跃响应可能会导致边界效应。这些效应在滤波器开始和结束时可能会更为显著。
通常情况下,信号处理中的边界效应是不可避免的,并且可能因滤波器类型、信号特性和截断方式而异。为了减轻这些效应,你可以考虑以下方法:
使用合适的边界处理:一种方法是在信号的开始和结束时应用边界处理技术**,如零填充**、周期延拓或反射延拓,以减少边界效应的影响。
使用长滤波器:使用更长的滤波器可以减少滤波器的有限长度效应,但也会增加计算成本。
谨慎选择滤波器类型:不同类型的滤波器在边界效应方面有不同的性质,因此根据具体应用的需要选择适当的滤波器类型。
考虑后处理:在滤波后,对信号的边界段进行后处理,以减小边界效应的影响。
综上所述,边界效应是信号处理中的常见问题,可以通过适当的处理方法和滤波器选择来减轻其影响。
为了最终得到完美的滤波器,我们可以考虑零相位滤波器,简单来说就是这种滤波器进行双向滤波一定程度上减少了边界效应。
直接上代码和结果文章来源:https://www.toymoban.com/news/detail-716556.html
# 开发时间:2023/10/25 22:22
# 开发内容:
# 运行环境:
# 备注内容:
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# 生成示例数据,包括噪声和带有干扰的信号
fs = 1000 # 采样频率
t = np.arange(0, 1, 1/fs)
fs =1000
t =np.arange(0,1,1/fs)
noise = 0.5 * np.sin(2 * np.pi * 50 * t) # 50 Hz噪声
signal_with_noise = np.sin(2 * np.pi * 5 * t) + noise # 5 Hz信号 + 50 Hz噪声
# 设计陷波滤波器来去除50 Hz干扰
f0 = 50.0 # 噪声的中心频率
Q = 0.2# 带宽-------------------------------------------修改之处
b, a = signal.iirnotch(f0, Q, fs)
# 使用滤波器来去除噪声--------------------------------------修改之处
filtered_signal = signal.filtfilt(b, a, signal_with_noise)
# 绘制原始信号和去噪后的信号
plt.figure(1)
plt.subplot(2, 1, 1)
plt.plot(t, signal_with_noise, 'b', label='带噪声的信号')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(t, filtered_signal, 'g', label='q=100')
plt.legend()
plt.tight_layout()
plt.show()
fs=1000
t =np.arange(0,1,1/fs)
signalwave =np.sin(2*np.pi*5*t)
plt.figure(2)
plt.plot(signalwave,label="5Hz-sin")
plt.legend()
plt.show()

效果已经很好那么我们要是使用截断法,可以截断尾部的信号。而且我们这个滤波之后的信号不存在相位移动。。文章来源地址https://www.toymoban.com/news/detail-716556.html
到了这里,关于【Python 算法】信号处理通过陷波滤波器准确去除工频干扰的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!