数据结构中的树与二叉树,是在建立非线性数据结构方面极为重要的两个概念。它们不仅能够模拟出生活中各种实际问题的复杂关系,还常被用于实现搜索、排序、查找等算法,甚至成为一些大型软件和系统中的基础设施。
无论你是初学者还是进阶者,本文将为你提供简单易懂、实用可行的知识点,帮助你更好地掌握树和二叉树在数据结构和算法中的重要性,进而提升算法解题的能力。接下来让我们开启数据结构与算法的奇妙之旅吧。
目录
树和森林的概念
树的常考性质
二叉树的定义及其性质
二叉树的表示
二叉树遍历
树和森林的概念
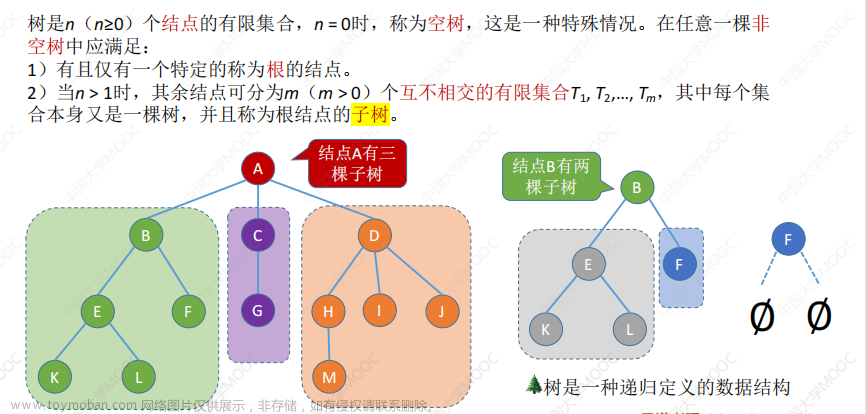
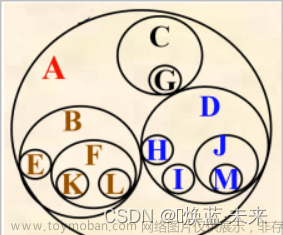
树的定义:树是一种非线性的数据结构,它由节点(node)和边(edge)组成。树的基本概念是以层次结构来组织和表示数据。
在树中,有一个特殊的节点被称为根节点(root),它是树的顶层节点,所有其他节点都直接或间接地与根节点相连。除了根节点外,每个节点可以有零个或多个子节点(child),子节点又可以有自己的子节点,形成了树的分支结构。没有子节点的节点被称为叶节点(leaf)或叶子节点,它们位于树的最底层。节点之间的连接称为边,边描述了节点之间的关系。每个节点可以有零条到多条边连接到其子节点。任意两个节点之间都存在唯一的路径,通过路径可以从一个节点到达另一个节点。
树的结构具有以下特点:
- 一个树可以由零个或多个节点组成。
- 有且只有一个根节点,它是树的起点。
- 每个节点可以有零个或多个子节点。
- 节点之间通过边相连,形成层次结构。
- 每个节点除了根节点外,都有且只有一个父节点。

树的基本术语:
结点之间的关系描述
根节点(Root Node):树的顶层节点称为根节点。根节点是树的起点,它没有父节点,其他所有节点都直接或间接地与根节点相连。
祖先节点(Ancestor Node):对于一个节点,它的所有上级节点(包括父节点、父节点的父节点等等)都被称为该节点的祖先节点。
子孙节点(Descendant Node):对于一个节点,它的所有下级节点(包括子节点、子节点的子节点等等)都被称为该节点的子孙节点。
父节点(Parent Node):一个节点的直接上一级节点称为其父节点。每个节点都可以有零个或多个子节点,但只能有一个父节点(除了根节点)。
子节点(Child Node):一个节点直接连接的下一级节点称为其子节点。一个节点可以有零个或多个子节点。
兄弟节点(Sibling Node):具有相同父节点的节点称为兄弟节点。兄弟节点在同一层级上。
叶节点(Leaf Node):也称为叶子节点,是没有子节点的节点,位于树的最底层。
层级(Level):根节点在第一层,其直接子节点在第二层,以此类推。一个节点所在的层级数即为该节点的层级。

结点、树的属性描述
节点值(Node Value):每个节点都可以携带一个值或数据,表示该节点所代表的实际含义或信息。
节点深度(Node Depth):节点深度指的是该节点到根节点的路径长度,即从根节点到该节点所经过的边的数量。根节点的深度为0。
节点高度(Node Height):节点高度指的是该节点到其最远叶节点的路径长度,即从该节点到达最远叶节点所经过的边的数量。叶节点的高度为0。
子树(Subtree):对于一个树中的节点,可以以该节点为根构成的子树称为该节点的子树。
树的大小(Tree Size):指的是树中包含的所有节点的总数。
树的高度(Tree Height):指的是树中任意节点的高度的最大值。也可以理解为从根节点到最远叶节点的路径长度的最大值。

有序树、无序树
有序树(Ordered Tree):有序树是指树中的子节点之间存在明确的顺序关系。在有序树中,每个子节点都有一个明确定义的位置,在遍历和表示树的时候需要按照顺序来考虑。例如,家谱树中的兄弟姐妹一般按照他们出生的先后顺序排列。
无序树(Unordered Tree):无序树是指树中的子节点之间没有明确的顺序关系。在无序树中,所有子节点都是平等的,没有先后之分。例如,文件系统中的目录结构就是一种无序树,其中的各个子目录之间没有特定的顺序。
有序树和无序树的区别在于子节点的排列方式。在有序树中,子节点的顺序很重要,会影响到树的结构和含义;而在无序树中,子节点的顺序并不重要,只需要知道它们是该节点的子节点即可。

森林
森林(Forest)是指由多棵树(Tree)组成的集合。简单来说,森林可以看作是多个独立的树的集合。
森林的特点在于其中的树之间是相互独立的,彼此之间没有直接的连接或关系。每棵树都可以独立地进行遍历和操作。
需要注意的是,森林和树的层次结构是不同的概念。树是一种层次结构,它具有唯一的根节点和从根节点到其他节点的确定路径;而森林则是多个独立的树的集合,在森林中任意两棵树之间没有直接的联系。

树的抽象数据类型:
树的抽象数据类型定义了对树进行操作的基本操作集合,包括以下常见操作:
1)创建树:创建一个空的树数据结构。
2)插入节点:在树中插入一个新节点,并建立节点之间的关系。
3)删除节点:从树中删除指定的节点,并调整节点之间的关系。
4)遍历树:按照特定的顺序访问树中的节点,例如先序遍历、中序遍历、后序遍历等。
5)查找节点:在树中查找指定的节点。
6)获取树的属性:获取树的高度、节点个数、根节点等属性信息。
树的抽象数据类型并不关注具体的实现方式,而是定义了可以对树进行的操作以及这些操作的预期行为。
回顾重点,其主要内容整理成如下内容:

树的常考性质
常见考点1:结点数 = 总度数 + 1
常见考点2:度为m的树、m叉树的区别
常见考点3:度为m的树第i层至多有 个结点 (i 1),同理m叉树第i层至多有 个结点 (i 1):
常见考点4:高度为h的m叉树至多有 个结点。
常见考点5:高度为h的m叉树至少有h个结点。高度为h度为m的树至少有h+m-1个结点。
常见考点6:具有n个结点的m叉树的最小高度为
高度最小的情况——所有结点都有m个孩子:
回顾重点,其主要内容整理成如下内容:

二叉树的定义及其性质
二叉树定义:
二叉树是n(n0)个结点的有限集合,其有以下两种情况:
1)为空二叉树,即 n = 0 的时候
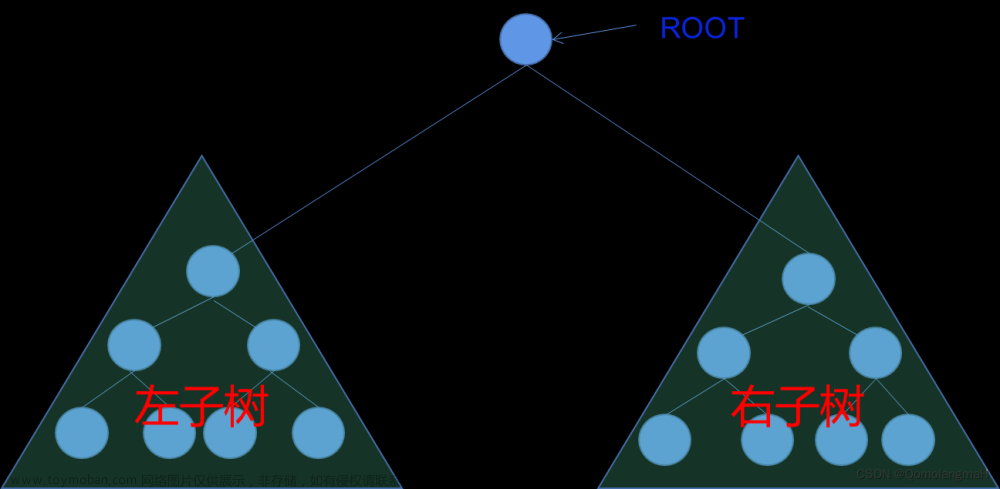
2)由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树又分别是一颗二叉树。
特点:每个结点至多只有两颗子树;左右子树不能颠倒。

二叉树的五种状态:

几个特殊的二叉树:
满二叉树:所有叶节点都在同一层,并且所有非叶节点都有两个子节点的二叉树称为满二叉树。
完全二叉树:除了最后一层节点之外,所有节点都拥有两个子节点,并且最后一层的节点都向左对齐的二叉树称为完全二叉树。

二叉排序树:(比如找关键字为60的结点)

平衡二叉树:树上任一结点的左子树和右子树的深度之差不超过1。

回顾重点,其主要内容整理成如下内容:

二叉树的常考性质:
常见考点1:设非空二叉树中度为0、1和2的结点个数分别为 ,则
叶子结点比二分支结点多一个
常见考点2:二叉树第i层至多有 个结点(i1);m叉树第i层至多有 个结点(i1)
常见考点3:高度为h的二叉树至多有 个结点(满二叉树)
高度为h的m叉树至多有 个结点
完全二叉树的常考性质:
常见考点1:具有n个(n>0)结点的完全二叉树的高度h为
或
常见考点2:对于完全二叉树,可以由结点数 n 推出度为 0、1和2的结点个数为、和
回顾重点,其主要内容整理成如下内容:

二叉树的表示
在数据结构中,二叉树可以通过数组表示和链表存储表示两种方式来实现。下面分别对这两种表示方式进行简述:
数组表示:
数组表示是将二叉树的节点按照某种方式存储在一个一维数组中。一般情况下,数组可以按照层次遍历的顺序存储二叉树的节点。假设根节点存储在数组下标为0的位置,那么对于任意一个节点的索引 i,其左子节点的索引为 2i+1,右子节点的索引为 2i+2。如果某个位置为空,可以使用特定的空值表示。
数组表示的优点:
数组表示的优点是存储简单,通过数组索引可以快速访问到任意节点。缺点是当二叉树的形状发生改变时,需要重新调整数组的大小,可能涉及到大量的元素移动。
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点结构体
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 构建二叉树的数组表示
struct TreeNode* build_binary_tree(int arr[], int size) {
struct TreeNode** tree = malloc(sizeof(struct TreeNode*) * size);
for (int i = 0; i < size; i++) {
if (arr[i] != -1) {
struct TreeNode* node = malloc(sizeof(struct TreeNode));
node->val = arr[i];
node->left = NULL;
node->right = NULL;
tree[i] = node;
} else {
tree[i] = NULL;
}
}
for (int i = 0; i < size; i++) {
if (tree[i] != NULL) {
if (2 * i + 1 < size)
tree[i]->left = tree[2 * i + 1];
if (2 * i + 2 < size)
tree[i]->right = tree[2 * i + 2];
}
}
struct TreeNode* root = tree[0];
free(tree);
return root;
}
// 测试代码
int main() {
int arr[] = {1, 2, 3, 4, 5, 6, 7};
int size = sizeof(arr) / sizeof(arr[0]);
struct TreeNode* root = build_binary_tree(arr, size);
// 输出测试结果
printf("root: %d\n", root->val);
printf("left child of root: %d\n", root->left->val);
printf("right child of root: %d\n", root->right->val);
return 0;
}链表存储表示:
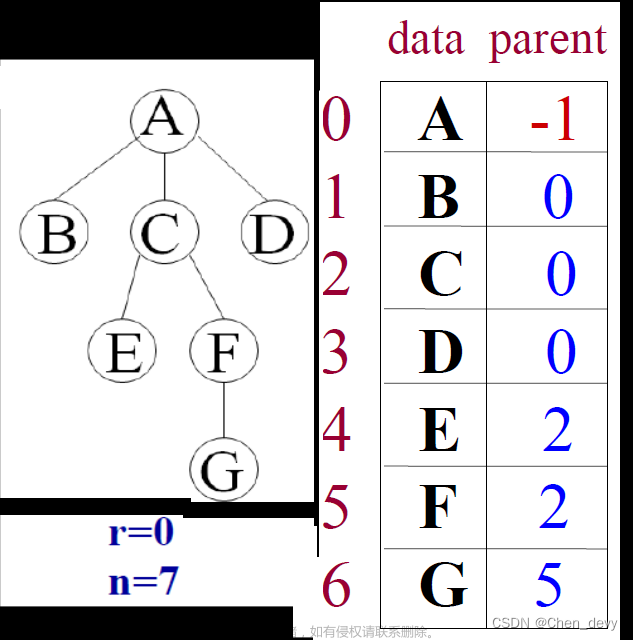
链表存储表示是使用链表的方式来表示二叉树。每个节点包含一个指向其父节点的指针,一个指向其左子节点的指针,一个指向其右子节点的指针。
链表存储表示的优点:
链表存储表示的优点是可以灵活地插入、删除节点而不需要移动其他节点,适用于频繁变化的二叉树结构。缺点是访问某个节点需要从根节点开始遍历,效率相对较低。
#include <stdio.h>
#include <stdlib.h>
// 二叉树节点结构体
struct TreeNode {
int val;
struct TreeNode* left;
struct TreeNode* right;
};
// 构建二叉树的链表存储表示
struct TreeNode* build_binary_tree(int arr[], int size) {
if (size == 0) {
return NULL;
}
struct TreeNode* root = malloc(sizeof(struct TreeNode));
root->val = arr[0];
root->left = NULL;
root->right = NULL;
struct TreeNode** queue = malloc(sizeof(struct TreeNode*) * size);
int front = 0;
int rear = 0;
queue[rear++] = root;
int i = 1;
while (i < size) {
struct TreeNode* node = queue[front++];
// 处理左子节点
if (arr[i] != -1) {
node->left = malloc(sizeof(struct TreeNode));
node->left->val = arr[i];
node->left->left = NULL;
node->left->right = NULL;
queue[rear++] = node->left;
}
i++;
// 处理右子节点
if (i < size && arr[i] != -1) {
node->right = malloc(sizeof(struct TreeNode));
node->right->val = arr[i];
node->right->left = NULL;
node->right->right = NULL;
queue[rear++] = node->right;
}
i++;
}
free(queue);
return root;
}
// 测试代码
int main() {
int arr[] = {1, 2, 3, 4, 5, 6, 7};
int size = sizeof(arr) / sizeof(arr[0]);
struct TreeNode* root = build_binary_tree(arr, size);
// 输出测试结果
printf("root: %d\n", root->val);
printf("left child of root: %d\n", root->left->val);
printf("right child of root: %d\n", root->right->val);
return 0;
}二叉树遍历
遍历:按照某种次序把所有结点都访问一遍。根据二叉树的递归特性要么是个空二叉树,要么就是由“根结点+左子树+右子树”组成的二叉树

根据二叉树的三种遍历规则,相关的具体案例如下:

再进行具体的练习一遍:


回顾重点,其主要内容整理成如下内容:

二叉树的层序(次)遍历:

其相应的代码实现如下:

由遍历序列构造二叉树:





回顾重点,其主要内容整理成如下内容: 文章来源:https://www.toymoban.com/news/detail-716709.html
 文章来源地址https://www.toymoban.com/news/detail-716709.html
文章来源地址https://www.toymoban.com/news/detail-716709.html
到了这里,关于数据结构--》解锁数据结构中树与二叉树的奥秘(一)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!