SPFA 算法：实现原理及其应用-Toy模板网

这篇具有很好参考价值的文章主要介绍了SPFA 算法：实现原理及其应用。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、前言

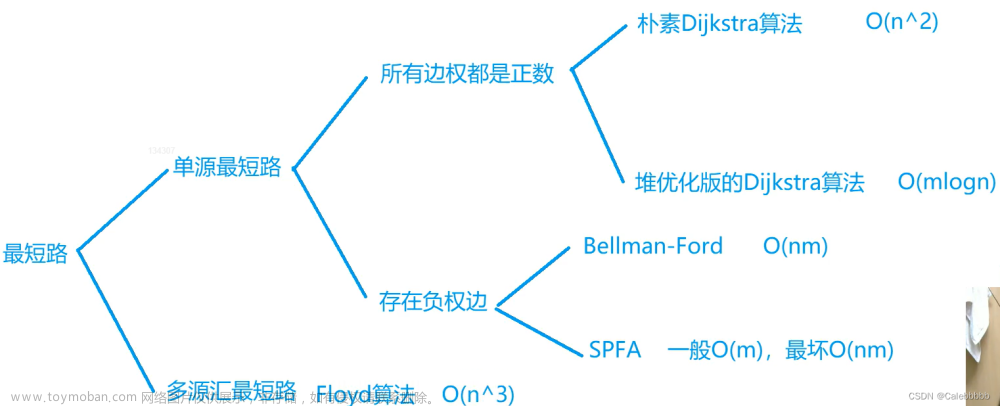
SPFA算法，全称为Shortest Path Faster Algorithm，是求解单源最短路径问题的一种常用算法，它可以处理有向图或者无向图，边权可以是正数、负数，但是不能有负环。

二、SPFA 算法

1、SPFA算法的基本流程

1. 初始化

首先我们需要起点s到其他顶点的距离初始化为一个很大的值（比如9999999，像是 JAVA 中可以设置 Integer.MAX_VALUE 来使），并将起点s的距离初始化为0。同时，我们还需要将起点s入队。

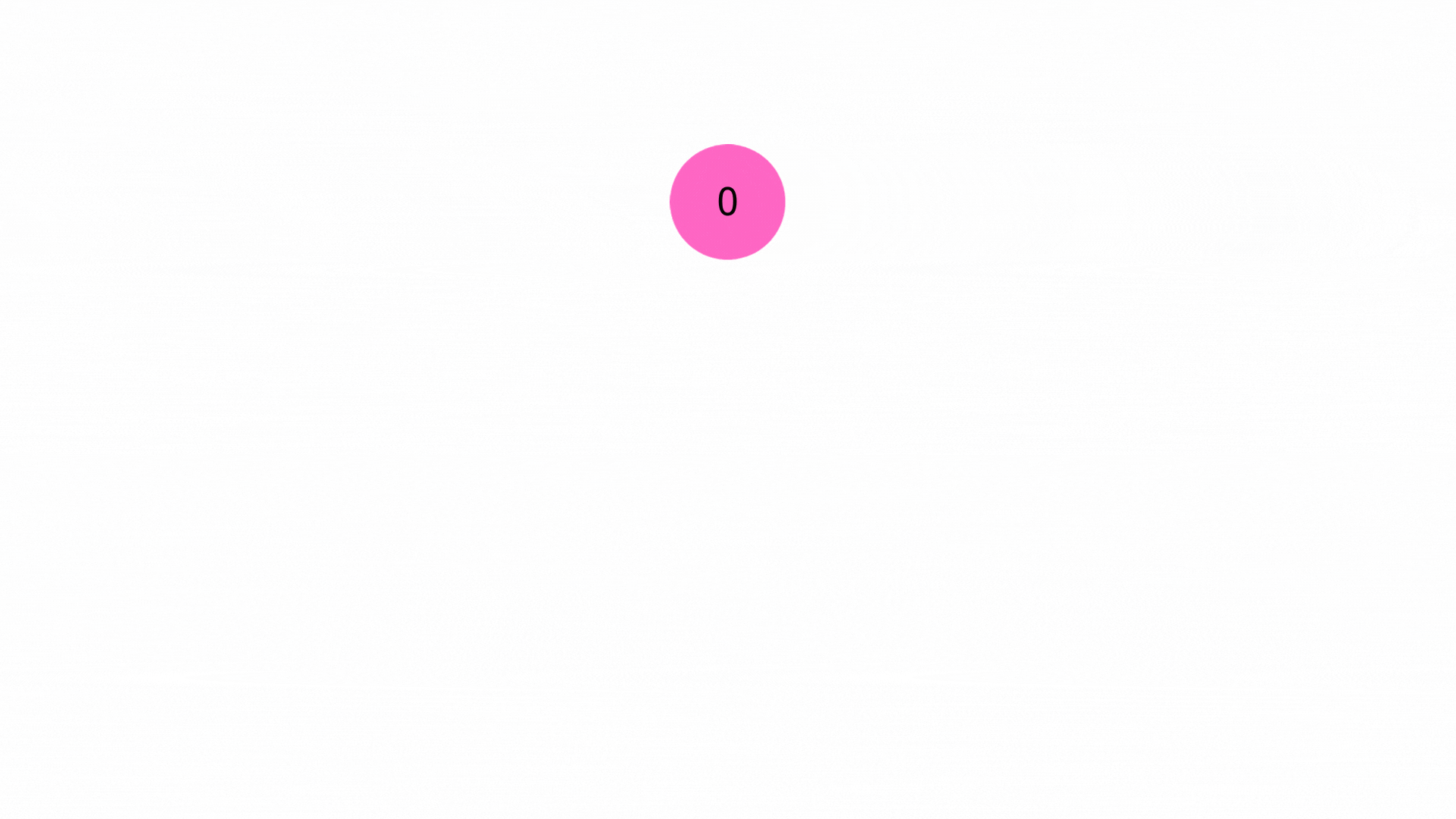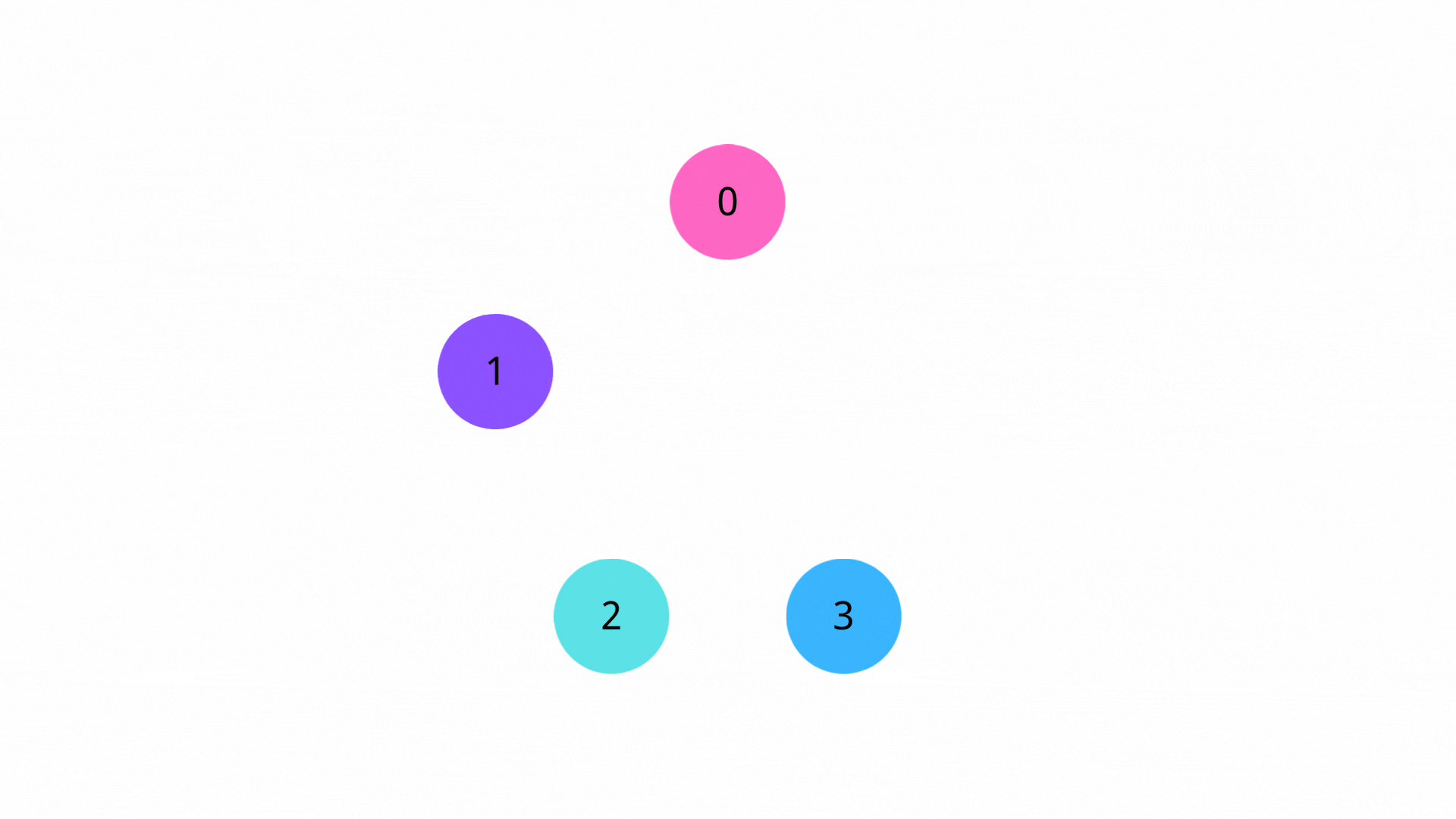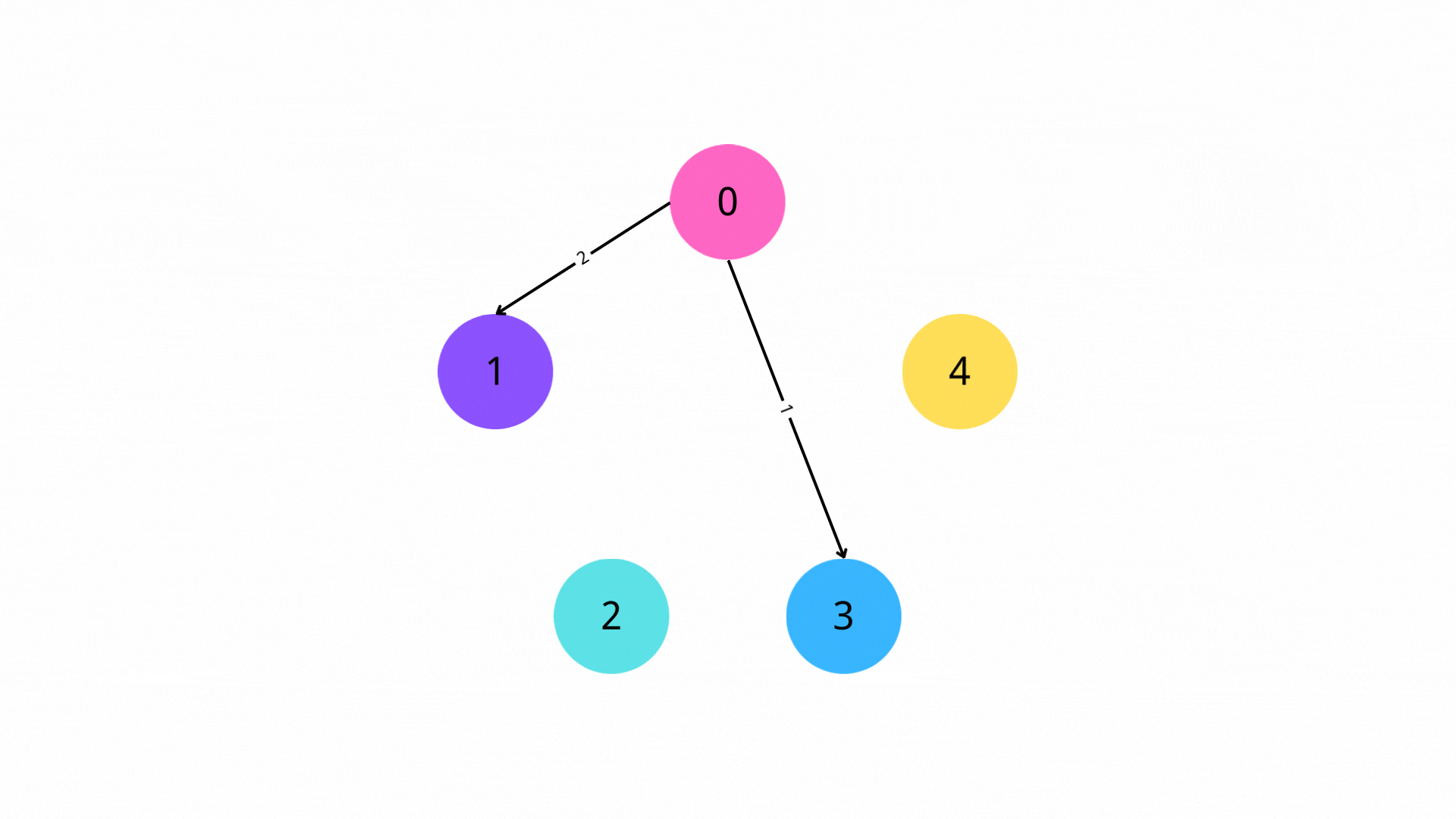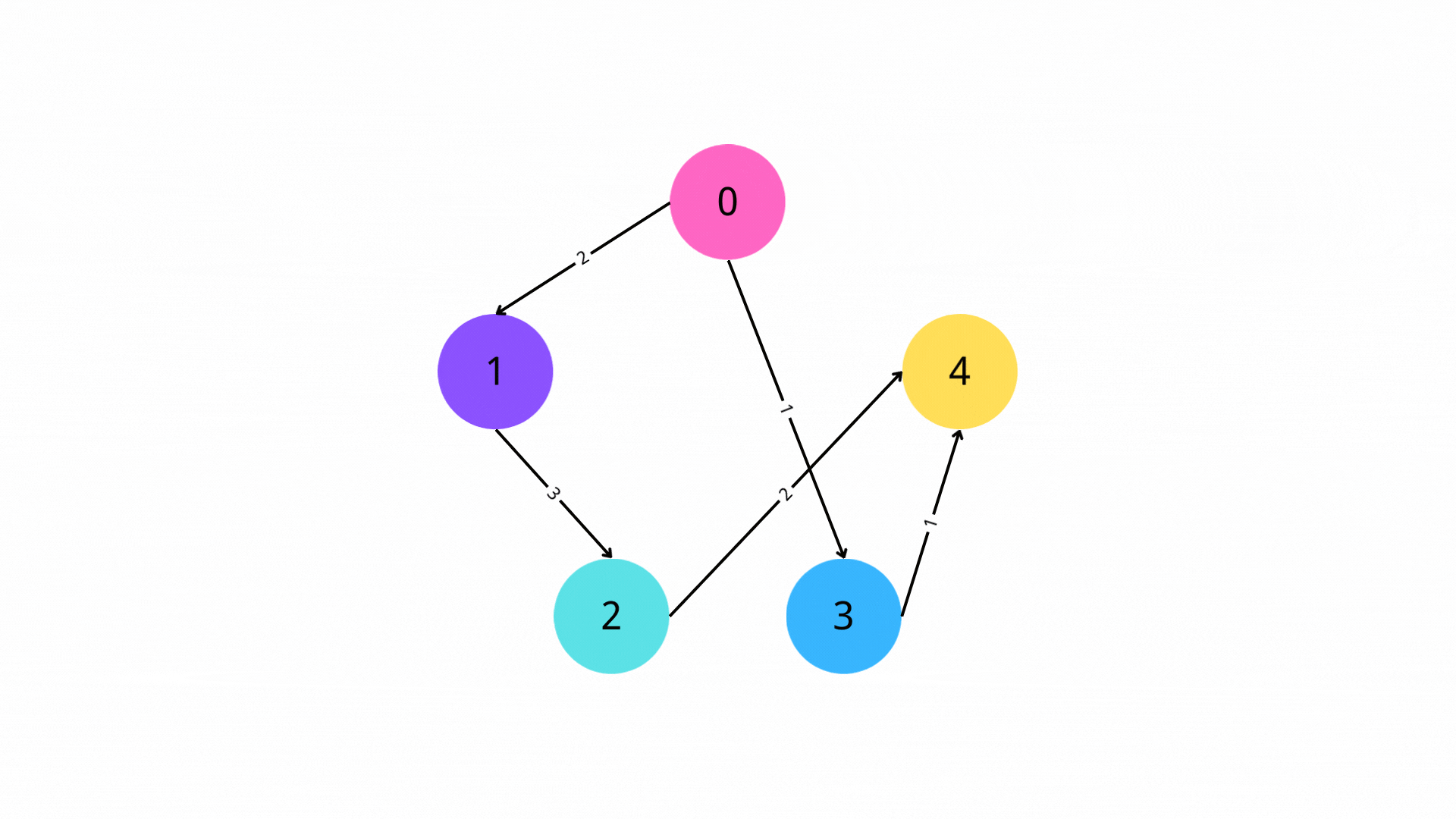
spfa,算法,算法,java,图论

2. 迭代

每次从队列中取出一个顶点u，遍历所有从u出发的边，对于边（u,v）（其中v为从u可以到达的顶点），如果s->u->v的路径长度小于s->v的路径长度，那么我们就更新s->v的路径长度，并将v入队。

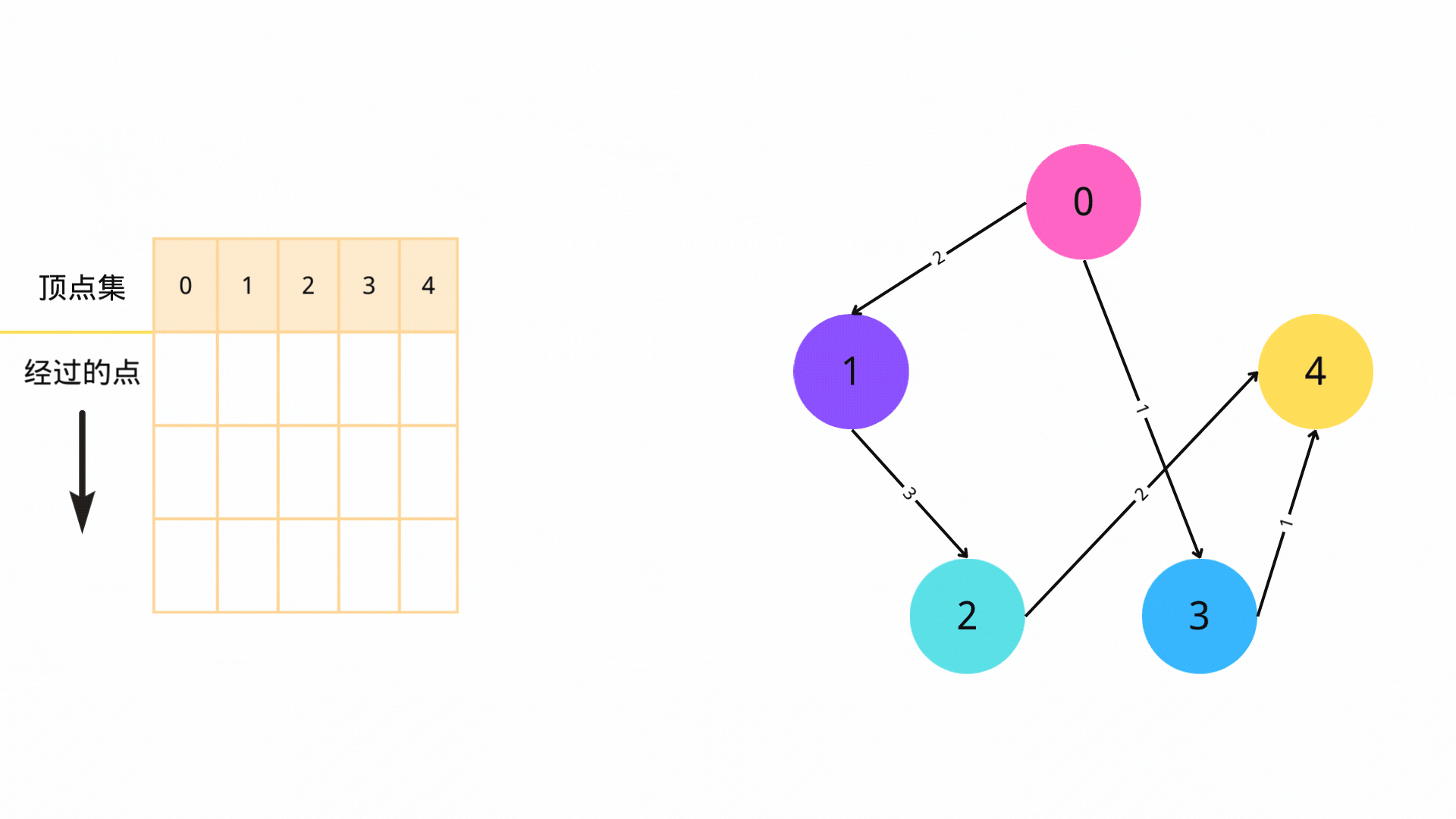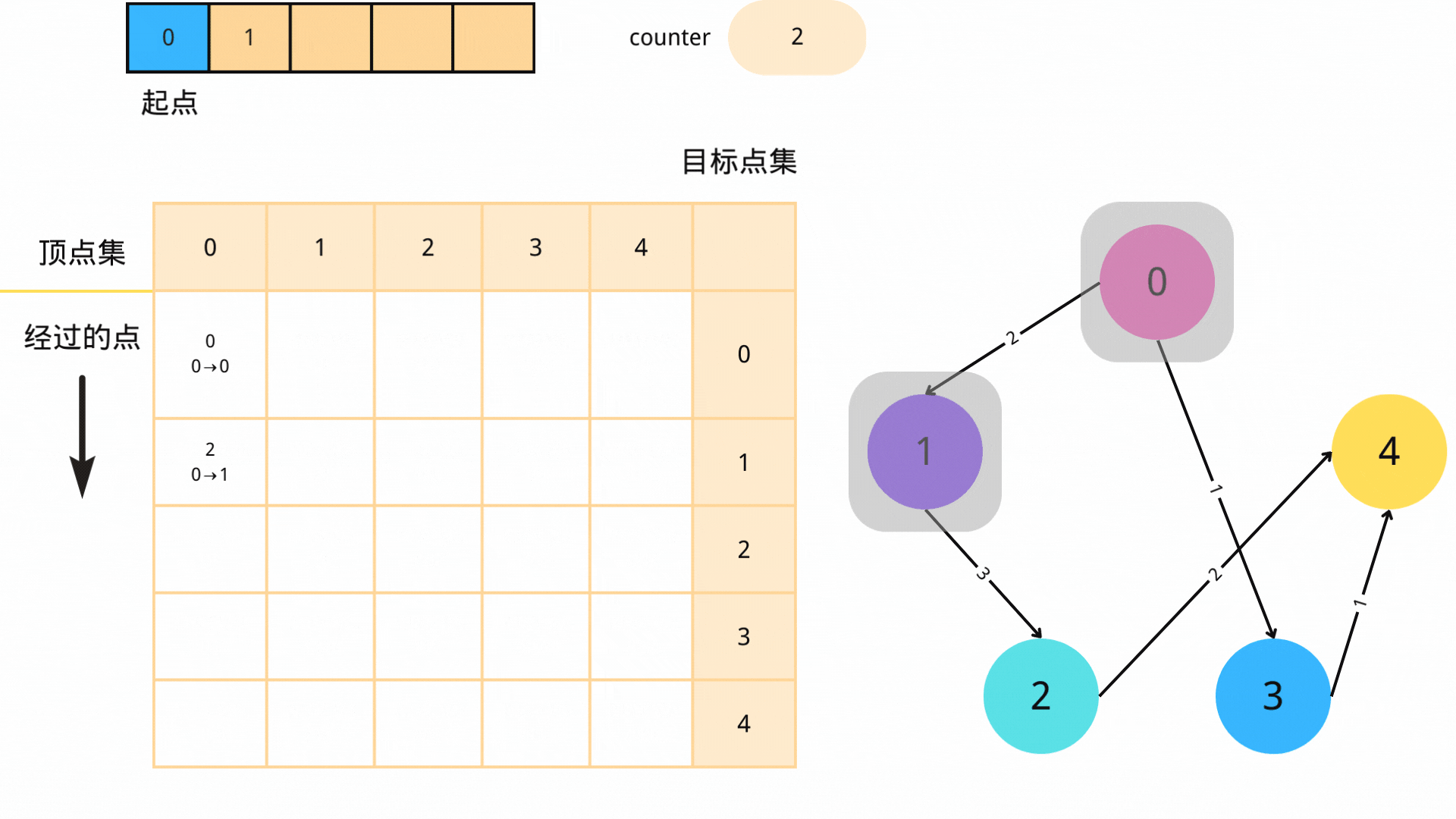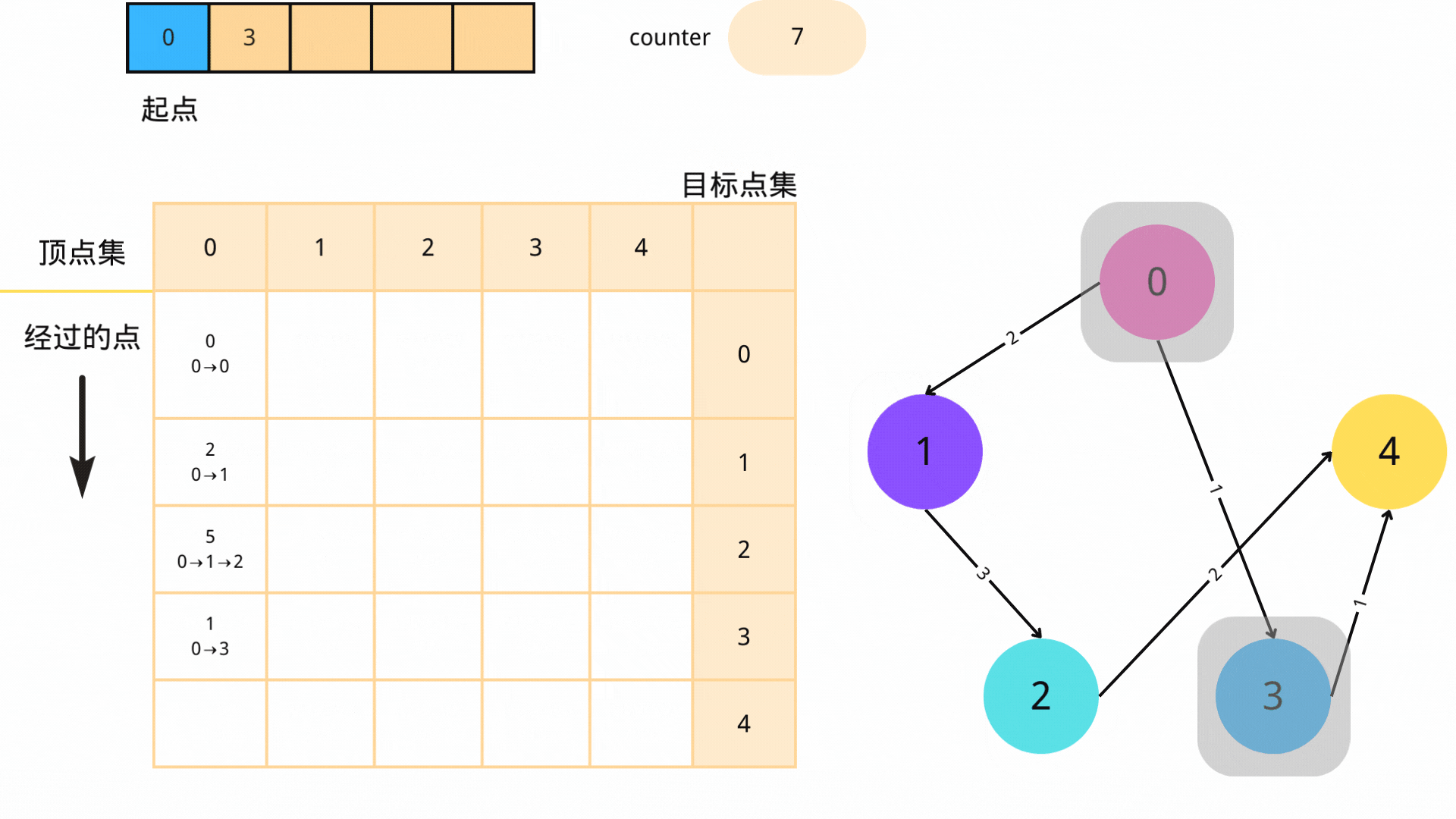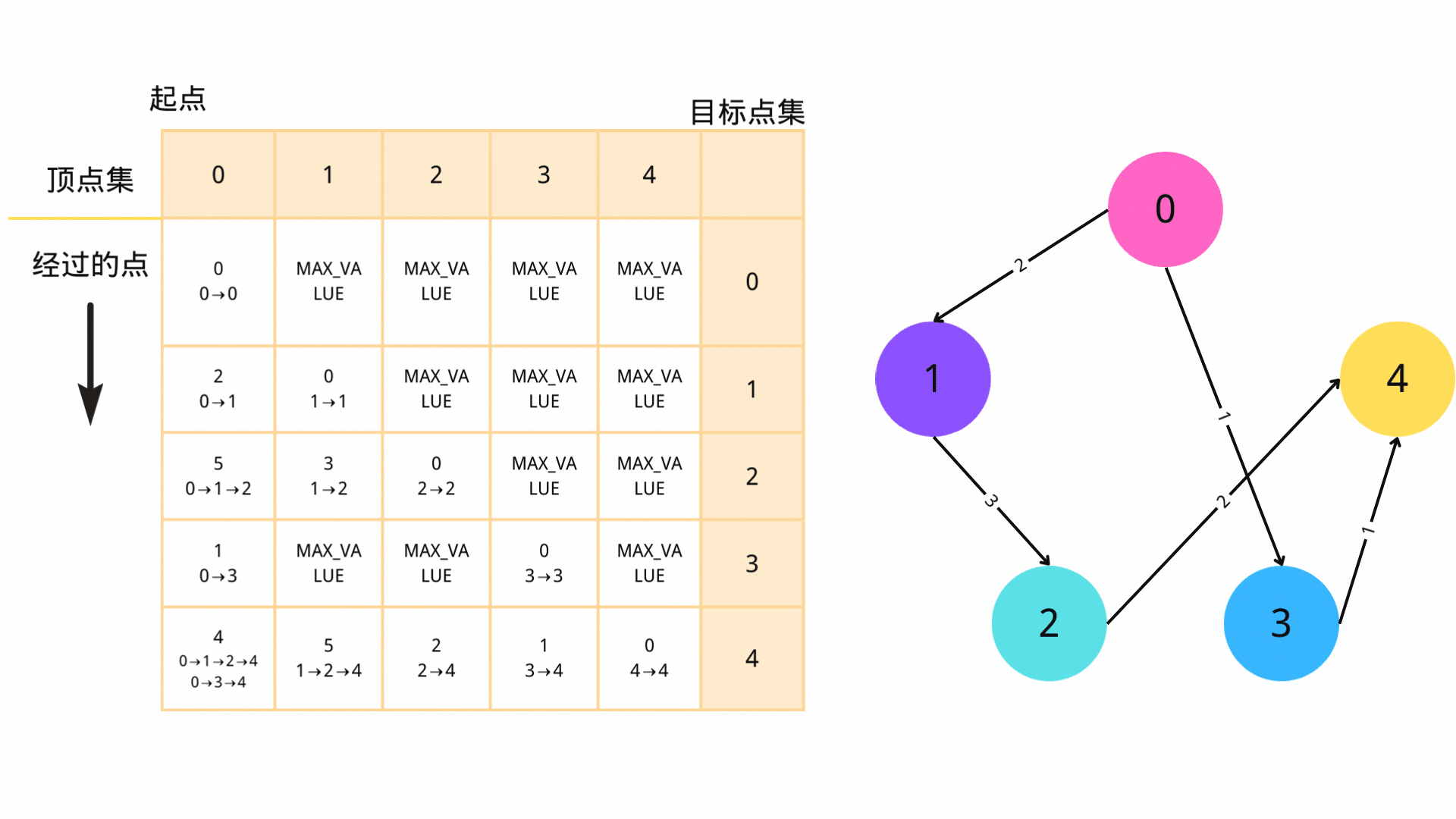
spfa,算法,算法,java,图论

3. 循环

不断进行步骤2，直到队列为空。

4. 判断

最后，我们可以得到从起点s到各个顶点的最短路径长度，如果存在无穷小的距离，则说明从起点s无法到达该顶点。

其次，需要注意的是，SPFA算法中存在负环问题。如果存在负环，则算法会陷入死循环。因此，我们需要添加一个计数器，记录每个点进队列的次数。当一个点进队列的次数超过图中节点个数时，就可以判定存在负环。

2、代码详解

以下是使用Java实现 SPFA算法的代码，其中Graph类表示有向图或无向图，Vertex类表示图中的一个顶点，Edge类表示图中的一条边。文章来源地址https://www.toymoban.com/news/detail-716927.html

import java.util.*;

class Graph {
      // 图
    private List<Vertex> vertices;  // 顶点集

    public Graph() {
   
        vertices = new ArrayList<Vertex>();
    }

    public void addVertex(Vertex v) {
      // 添加顶点
        vertices.add(v);
    }   // 添加顶点

    public List<Vertex> getVertices() {
    // 返回顶点
        return vertices;
    }   // 获取顶点集
}

class Vertex {
     // 点
    private int id; // 点 id
    private List<Edge> edges;   // 连接到该顶点的边
    private int distance;   // 从源顶点到该顶点的最短距离，MAX_VALUE init
    private boolean visited;    // 在图的遍历过程中是否访问过该顶点，false init

    public Vertex(int id) {
   
        this.id = id;
        edges = new ArrayList<Edge>();
        distance = Integer.MAX_VALUE;
        visited = false;
    }