【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一，二叉树的销毁

二，二叉树系列所有源代码

BTee.h

BTee.c

Queue.h

Queue.c

一，二叉树的销毁

【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）,数据结构,开发语言,算法,c语言,排序算法

二叉树建好了，利用完了，也该把申请的动态内存空间给释放了，那要如何释放呢？

【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）,数据结构,开发语言,算法,c语言,排序算法

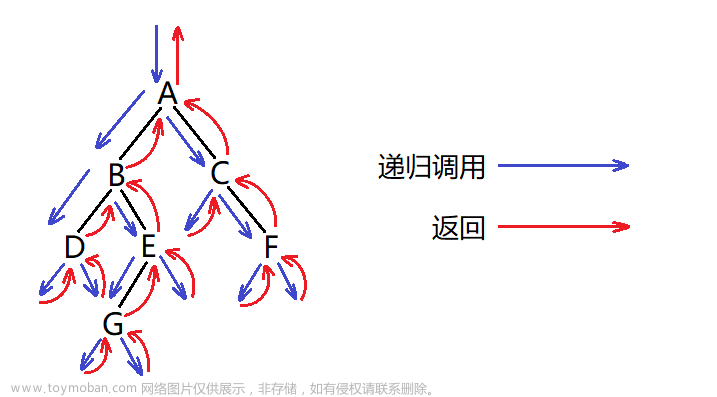
我们还是以这棵树为例，要把这棵树销毁掉，其实就是把树上的结点全部释放掉，但是呢这个释放的顺序挺讲究的，对于树，我们的思想首先就是，前序遍历，中序遍历，后序遍历，层序遍历的思想，那这棵树到底用什么思想好呢？

我们先来分析一下，要释放以（1）为根结点的树就相当于释放左子树（2）和右子树（4）和自身的结点，然后呢以（2），（4）为根结点的树也是同理，层层递归下去，这不就符合后序遍历的思想吗，先左子树-->右子树-->根结点！所以销毁这棵树的思路就是后序遍历的思路！

既然思路已经确定了，我们就要开始实现了！

大事化小：先释放结点的左子树，再释放其右子树然后在释放本身结点！

结束条件：当结点为空时返回 NULL ；

源代码：

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
    //判空
	if (root == NULL)
	{
		return NULL;
	}
    //释放左子树
	BinaryTreeDestory(root->left);
    //释放右子树
	BinaryTreeDestory(root->right);
    //释放本身结点
	free(root);
}

这就 ok 了，只要捋清楚思路了，就很简单了；

【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）,数据结构,开发语言,算法,c语言,排序算法

经过了9个阶段的学习，二叉树的初阶部分也是迎来了结尾，为什么说是初阶部分呢？因为一些更复杂的树的内容不太方便用 c 语言来讲解展示，等后面博主介绍完了 c++ 再来絮叨絮叨，同志们莫急，革命的道路还需一步一步向前走！

【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）,数据结构,开发语言,算法,c语言,排序算法

二，二叉树系列所有源代码

我们总共历经了九个阶段的学习，二叉树已是随便拿捏了！下面是这九个阶段以及二叉树初阶部分的所以源代码：

BTee.h

#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>

typedef int BTDataType;
//二叉链
typedef struct BinaryTreeNode
{
	BTDataType data; // 当前结点值域	
	struct BinaryTreeNode* left; // 指向当前节点左孩子
	struct BinaryTreeNode* right; // 指向当前节点右孩子
}BTNode;

//动态创立新结点
BTNode* BuyNode(BTDataType x);
//创建二叉树
BTNode* GreatBTree();
//前序遍历
void PrevOrder(BTNode* root);
//中序遍历
void InOrder(BTNode* root);
//后序遍历
void PostOrder(BTNode* root);
//结点个数
int	SumNode(BTNode* root);
//叶子结点个数
int LeafNode(BTNode* root);
//二叉树高度
int HeightTree(BTNode* root);
//二叉树第k层结点个数
int BTreeLeveSize(BTNode* root, int k);
//二叉树查找值为x的结点
BTNode* BTreeFine(BTNode* root, int x);
//层序遍历
void LevelOrder(BTNode* root);
//二叉树的销毁
void BinaryTreeDestory(BTNode* root);
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BTCreate(BTDataType* a,int* i);
// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root);

BTee.c

#define _CRT_SECURE_NO_WARNINGS 1
#include"BTree.h"
#include"Queue.h"
//动态创立新结点
BTNode* BuyNode(BTDataType x)
{
	BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
	assert(newnode);
	newnode->data = x;
	newnode->left = NULL;
	newnode->right = NULL;
	return newnode;
}

//创建二叉树
BTNode* GreatBTree()
{
	BTNode* node1 = BuyNode(1);
	BTNode* node2 = BuyNode(2);
	BTNode* node3 = BuyNode(3);
	BTNode* node4 = BuyNode(4);
	BTNode* node5 = BuyNode(5);
	BTNode* node6 = BuyNode(6);

	node1->left = node2;
	node1->right = node4;
	node2->left = node3;
	node4->left = node5;
	node4->right = node6;

	return node1;
}

//前序遍历
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

//中序遍历
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return NULL;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

//后序遍历
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("N ");
		return;
	}

	PostOrder(root->left);
	PostOrder(root->right);
	printf("%d ", root->data);
}


//结点个数
int SumNode(BTNode* root)
{
	return root == NULL ? 0 : SumNode(root->left) + SumNode(root->right) + 1;
}

//叶子结点个数
int LeafNode(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (root->left==NULL && root->right==NULL)
	{
		return 1;
	}
	else
	{
		return LeafNode(root->left) + LeafNode(root->right);
	}
}

//二叉树高度
int HeightTree(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int left = HeightTree(root->left);
	int right = HeightTree(root->right);
	return left > right ? left + 1 : right + 1;
}

//二叉树第k层结点个数
int BTreeLeveSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}
	if (k == 1)
	{
		return 1;
	}
	return BTreeLeveSize(root->left, k - 1)  + BTreeLeveSize(root->right, k - 1);
}

//二叉树查找值为x的结点
BTNode* BTreeFine(BTNode* root, int x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->data == x)
	{
		return root;
	}
	if (BTreeFine(root->left, x) == NULL)
	{
		return BTreeFine(root->right, x);
	}
	else
	{
		return BTreeFine(root->left, x);
	}
}

//层序遍历
void LevelOrder(BTNode* root)
{
	Queue q;
	// 初始化队列 
	QueueInit(&q);
	// 队尾入队列 
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		printf("%d ", QueueFront(&q)->data);
		BTNode* cur = QueueFront(&q);
		// 队头出队列
		QueuePop(&q);
		if (cur->left)
		{
			QueuePush(&q, cur->left);
		}
		if (cur->right)
		{
			QueuePush(&q, cur->right);
		}
	}
}

//二叉树的销毁
void BinaryTreeDestory(BTNode* root)
{
	//判空
	if (root == NULL)
	{
		return NULL;
	}
	//释放左子树
	BinaryTreeDestory(root->left);
	//释放右子树
	BinaryTreeDestory(root->right);
	//释放本身结点
	free(root);
}

void _BinaryTreeCreate(BTNode* node, BTDataType* a,int* pi)
{
	if (node == NULL)
	{
		return;
	}
	node->left= BuyNode(a[(*pi)++]);
	node->right= BuyNode(a[(*pi)++]);
}

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{
	if (a == NULL)
	{
		return NULL;
	}
	BTNode* node1= BuyNode(a[(*pi)++]);
	_BinaryTreeCreate(node1, a, pi);
	return node1;
}

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BTCreate(BTDataType* arr, int*i)
{
	if (arr[(*i)] == '#')
	{
		(*i)++;
		return NULL;
	}
	BTNode* root = BuyNode(arr[(*i)++]);
	root->left = BTCreate(arr, i);
	root->right = BTCreate(arr, i);
	return root;
}

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(BTNode* root)
{
	Queue q;
	// 初始化队列 
	QueueInit(&q);
	// 队尾人队列 
	QueuePush(&q,root);
	while(QueueFront(&q))
	{
		BTNode* cur = QueueFront(&q);
		// 队头出队列 
		QueuePop(&q);
		QueuePush(&q, cur->left);
		QueuePush(&q, cur->right);
	}
	while (!QueueEmpty(&q))
	{
		// 队头出队列 
		QueuePop(&q);
		if (QueueFront(&q) != NULL)
		{
			BinaryTreeDestory(root);
			return 0;
		}
	}
	return 1;
}

下面是【栈】的源代码，二叉树的层序遍历用的着，这边也发给大家了：

Queue.h

#define _CRT_SECURE_NO_WARNINGS 1
#pragma once
#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include"BTree.h"

typedef BTNode* QDataType;
//结点
typedef struct QListNode
{
	struct QListNode* next;
	QDataType data;
}QNode;

// 队列
typedef struct Queue
{
	QNode* front; // 队头
	QNode* rear; //队尾
	int size;
}Queue;

// 初始化队列 
void QueueInit(Queue* q);
// 队尾人队列 
void QueuePush(Queue* q, QDataType data);
// 队头出队列 
void QueuePop(Queue* q);
// 获取队列头部元素 
QDataType QueueFront(Queue* q);
// 获取队列队尾元素 
QDataType QueueBack(Queue* q);
// 获取队列中有效元素个数 
int QueueSize(Queue* q);
// 判空
int QueueEmpty(Queue* q);
// 销毁队列 
void QueueDestroy(Queue* q);

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1
#define _CRT_SECURE_NO_WARNINGS 1
#include"Queue.h"

// 初始化队列 
void QueueInit(Queue* q)
{
	assert(q);
	q->front = q->rear = NULL;
	q->size = 0;
}

// 队尾入队列 
void QueuePush(Queue* q, QDataType data)
{
	assert(q);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(-1);
	}
	newnode->next = NULL;
	newnode->data = data;
	if (q->front /*= q->rear*/ == NULL)//谨记判断不要用此等格式
	{
		q->front = q->rear = newnode;
	}
	else
	{
		q->rear->next = newnode;
		q->rear = newnode;
	}
	q->size++;
}
// 队头出队列 
void QueuePop(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	if (q->front->next == NULL)
	{
		free(q->front);
		q->front = q->rear = NULL;
	}
	else
	{
		QNode* next = q->front->next;
		free(q->front);
		q->front = next;
	}
	q->size--;
}
// 获取队列头部元素 
QDataType QueueFront(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->front->data;
}
// 获取队列队尾元素 
QDataType QueueBack(Queue* q)
{
	assert(q);
	assert(!QueueEmpty(q));
	return q->rear->data;
}
// 获取队列中有效元素个数 
int QueueSize(Queue* q)
{
	assert(q);
	return q->size;
}
// 检测队列是否为空，如果为空返回非零结果，如果非空返回0 
int QueueEmpty(Queue* q)
{
	assert(q);
	return q->size == 0;
}
// 销毁队列 
void QueueDestroy(Queue* q)
{
	assert(q);

	QNode* cur = q->front;
	QNode* next = NULL;
	while (cur)
	{
		next = cur->next;
		free(cur);
		cur = next;
	}
	cur = NULL;
	q->rear = NULL;
}

同志们！二叉树（初阶）的知识就到这了，加油！

【数据结构】二叉树的销毁 & 二叉树系列所有源代码（终章）,数据结构,开发语言,算法,c语言,排序算法