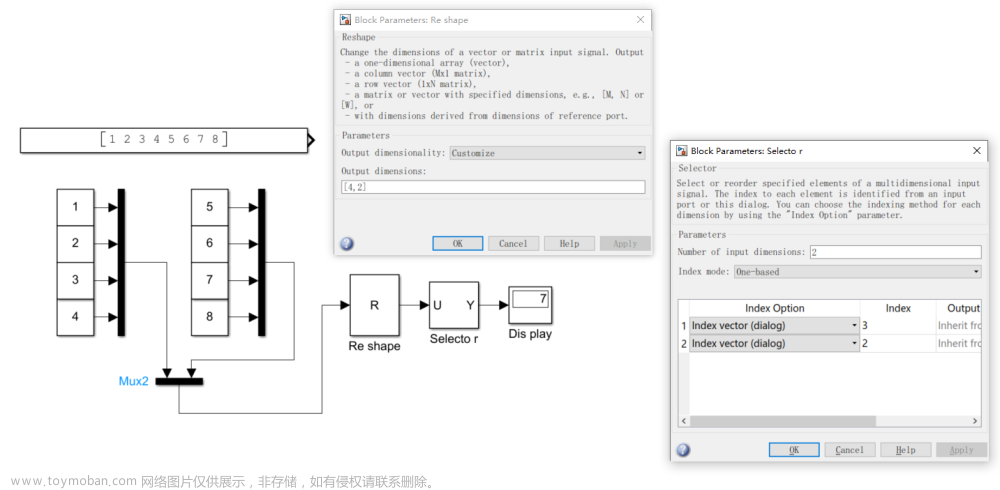
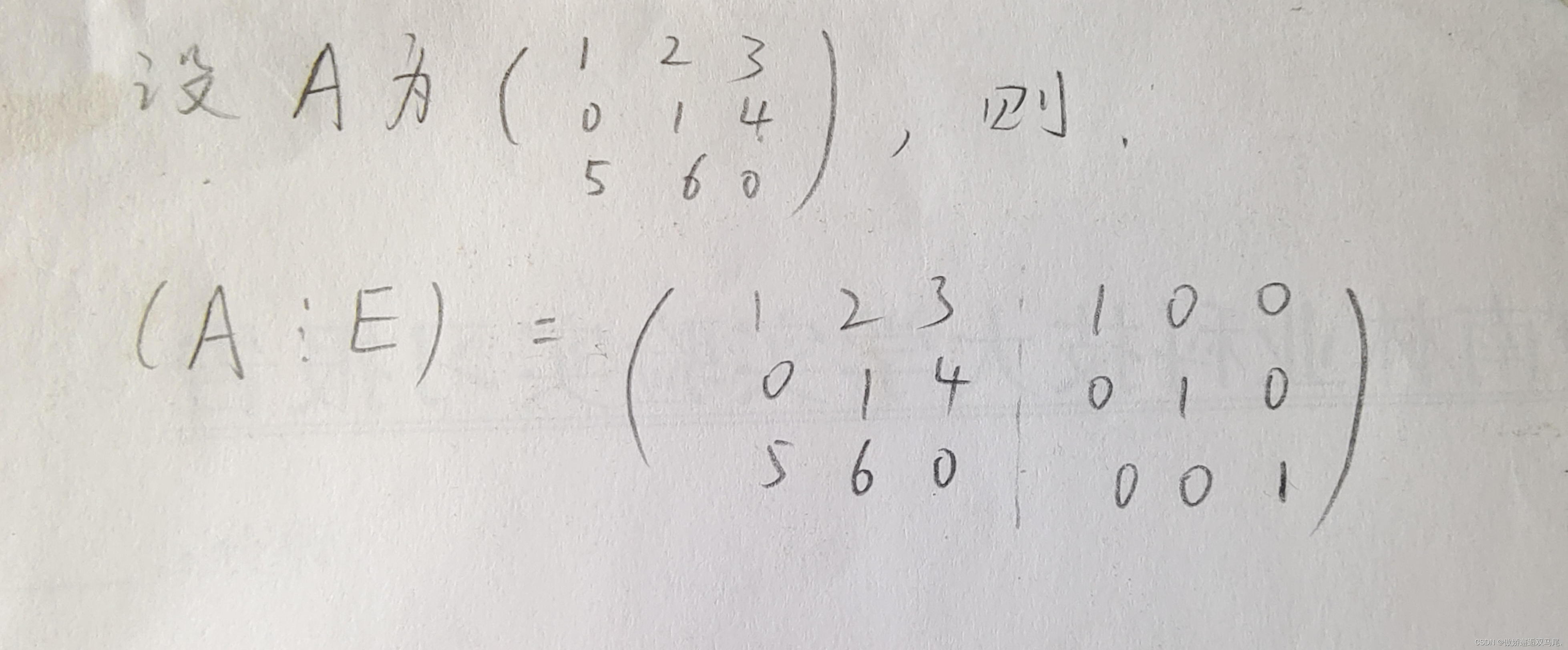C语言实现矩阵求逆（四阶）-Toy模板网

这篇具有很好参考价值的文章主要介绍了C语言实现矩阵求逆（四阶）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

伴随矩阵和代数余子式法
高斯消元法
LU分解

前言：本文讲述伴随矩阵求逆，其余方法有时间会加以整理。
参考：
代码实现矩阵求逆的三种方式
矩阵的行列式

1. 伴随矩阵和代数余子式法

1.1 原理

求一个四阶矩阵的逆矩阵要多久,C语言,c语言,矩阵,算法
文章来源地址https://www.toymoban.com/news/detail-717735.html

1.2 代码

#include <stdio.h>
#include <math.h>
typedef unsigned char uint8;

//全局变量定义
uint8 MatrixSize=4;
double AdjMatrix[4][4] = { 0 };
double detA4 = 0;
//函数声明
double GetdetA3(double matrix[3][3]);
void Adj_matrix4(double* matrix);


int  main()
{
	printf("Hello!");
	double matrixtest[4][4] = {{6,5,-9,6},{2,0,-4,8},{-1,4,2,2},{2,-10,0,-10}};
	double det = 0;
	double InvMtrx[4][4] = { 0 };
	Adj_matrix4(&matrixtest[0][0]);
	if (detA4 == 0) return;
	else {
		for (uint8 i = 0; i < 4; i++) {
			for (uint8 j = 0; j < 4; j++) {
				InvMtrx[i][j] = AdjMatrix[i][j] / detA4;
			}
		}
	}
	return 0;
}
//MatrixSize;	MatrixSize = sizeof matrix / sizeof matrix[0];
double GetdetA3(double matrix[3][3])
{
	double detA3 = 0;
	detA3 = matrix[0][0] * matrix[1][1] * matrix[2][2] + matrix[0][1] * matrix[1][2] * matrix[2][0] + matrix[0][2] * matrix[1][0] * matrix[2][1]
		- matrix[0][2] * matrix[1][1] * matrix[2][0] - matrix[0][1] * matrix[1][0] * matrix[2][2] - matrix[0][0] * matrix[1][2] * matrix[2][1];
	return detA3;
}

//四阶矩阵的伴随矩阵
void Adj_matrix4(double *matrix){
	double tmp[3][3] = { {0} ,{0} ,{0} };
	for(uint8 row = 0; row < 4; row++){
		for (uint8 colm = 0; colm < 4; colm++){
			//求第row、colm余子式矩阵
			uint8 k=0, p = 0;
			for (uint8 i = 0; i < 3;i++ ) {
				if (i == colm) p++;
				for (uint8 j = 0;j < 3; j++ ) {
					if (j == row) k++;
					tmp[i][j] = *(matrix +k+4*p+j);
				}
				k = 0;
				p++;
			}
			//求余子式矩阵行列式
			double C_0colm = GetdetA3(tmp);
			//求出相应的代数余子式
			AdjMatrix[row][colm] = pow(-1, row + colm) * C_0colm;
			if (row==0) detA4 = detA4 + (* (matrix + row + colm * 4))* AdjMatrix[row][colm];
		}
	}
}