在西瓜数据集上用Python实现ID3决策树算法完整代码-Toy模板网

这篇具有很好参考价值的文章主要介绍了在西瓜数据集上用Python实现ID3决策树算法完整代码。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在西瓜数据集上用Python实现ID3决策树算法完整代码

1、决策树算法代码ID3.py

import operator
from math import log2
import visual_decision_tree


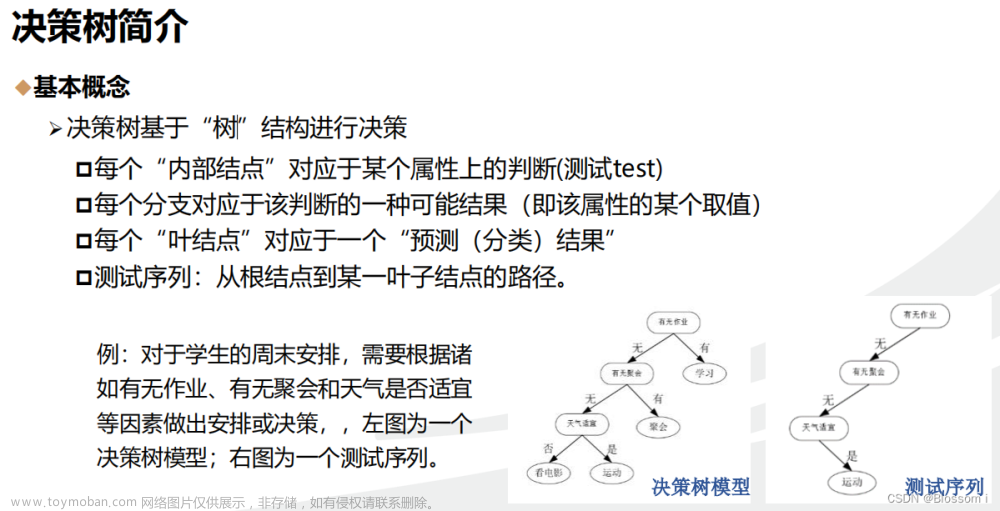
def createDataSet():
    # 数据集D
    dataSet = [['青绿', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
               ['乌黑', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
               ['乌黑', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
               ['青绿', '蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '好瓜'],
               ['浅白', '蜷缩', '浊响', '清晰', '凹陷', '硬滑', '好瓜'],
               ['青绿', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '好瓜'],
               ['乌黑', '稍蜷', '浊响', '稍糊', '稍凹', '软粘', '好瓜'],
               ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '硬滑', '好瓜'],
               ['乌黑', '稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜'],
               ['青绿', '硬挺', '清脆', '清晰', '平坦', '软粘', '坏瓜'],
               ['浅白', '硬挺', '清脆', '模糊', '平坦', '硬滑', '坏瓜'],
               ['浅白', '蜷缩', '浊响', '模糊', '平坦', '软粘', '坏瓜'],
               ['青绿', '稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '坏瓜'],
               ['浅白', '稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '坏瓜'],
               ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘', '坏瓜'],
               ['浅白', '蜷缩', '浊响', '模糊', '平坦', '硬滑', '坏瓜'],
               ['青绿', '蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '坏瓜']]

    # 属性集A
    labels = ['色泽', '根蒂', '敲声', '纹理', '脐部', '触感']
    return dataSet, labels


# 计算信息熵
def calcShannonEnt(dataSet):
    # 返回数据集的行数
    numDataSet = len(dataSet)
    # 保存每个标签的出现次数的字典
    lableCounts = {}
    # 对每组特征向量进行统计
    for featVec in dataSet:
        # 提取标签信息
        currentLable = featVec[-1]
        # 如果标签未放入统计次数字典，添加进去，初始值0
        if currentLable not in lableCounts.keys():
            lableCounts[currentLable] = 0
        # 样本标签计数
        lableCounts[currentLable] += 1
    infoEntropy = 0.0
    # 计算信息熵
    for key in lableCounts:
        # 当前样本集合中第k类样本所占的比例(指的是标签那一栏，例如：好瓜和坏瓜的占比)
        pk = float(lableCounts[key]) / numDataSet
        # 公式计算信息熵
        infoEntropy -= pk * log2(pk)
    return infoEntropy


# 按照特征属性划分数据集
def splitDataSet(dataSet, i, value):
    # 创建返回的数据集列表
    retDataSet = []
    # 遍历数据集（即所取的数据集的某一列）
    for featVec in dataSet:
        # 如果有这个属性，就操作对应的这一行数据
        if featVec[i] == value:
            # 这一行数据去掉i属性
            reducedFeatVec = featVec[:i]
            reducedFeatVec.extend(featVec[i + 1:])
            # 将去掉i属性的每一行数据，合并起来形成一个新的数据集、
            # 它的行数，即len()长度就是它占总体数据集的比重
            retDataSet.append(reducedFeatVec)
            # 返回划分后的数据集
    return retDataSet


# 选择最优划分属性
def selectBestFeatureToSplit(dataSet, i):
    print("*" * 20)
    print("第%d次划分" % i)
    # 特征的数量
    numFeatures = len(dataSet[0]) - 1
    # 数据集D的信息熵
    baseEntropy = calcShannonEnt(dataSet)
    # 信息增益
    bestInfoGain = 0.0
    # 最优属性的索引值
    bestFeature = -1
    # 遍历所有的特征值
    for i in range(numFeatures):
        # 遍历dataSize数据集中的第i个特征属性
        featList = [example[i] for example in dataSet]  # 二维数组按列访问属性
        uniqueVals = set(featList)  # set集合中存储不重复的属性元素
        newEntropy = 0.0  # Dv的信息熵（分支结点属性的信息熵）
        # 对每一个特征属性计算信息增益
        for value in uniqueVals:
            # subDataSet是每个特征按照其几种不同的属性划分的数据集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算分支结点的权重，也就是子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            # 计算赋予了权重的分支结点的信息熵的和
            newEntropy += prob * calcShannonEnt(subDataSet)
        # 第i个属性的信息增益
        infoGain = baseEntropy - newEntropy
        # 打印属性对应的信息增益
        print("\"%s\"特征的信息增益为%.3f" % (labels[i], infoGain))
        # 寻找最优的特征属性
        if infoGain > bestInfoGain:
            # 更新最优属性的信息熵和索引值
            bestInfoGain = infoGain
            bestFeature = i
    print("bestInfoGain: %.3f" % bestInfoGain)
    # 返回最优属性（最大信息增益）的索引值
    print("本次划分的最优属性是：%s" % labels[bestFeature])
    return bestFeature


# 统计classList中出现次数最多的元素（标签）
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
    # 根据字典的值降序排序
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1),
                              reverse=True)
    # 返回classList中出现次数最多的元素
    return sortedClassCount[0][0]


"""
函数说明:递归构建决策树
Parameters:
    dataSet - 训练数据集
    labels - 分类属性标签
    featLabels - 存储选择的最优特征标签
Returns:
    myTree - 决策树
"""


# 准备工作完成，开始递归构建决策树myTree
def createTree(dataSet, labels, featLabels, i):
    i += 1
    # 取分类标签(好瓜or坏瓜)
    classList = [example[-1] for example in dataSet]
    # 如果类别完全相同则停止继续划分，最后输出是好瓜还是坏瓜
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 遍历完所有特征时返回出现次数最多的类标签
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # select返回最优特征的索引值，bestFeat获取的是索引值
    bestFeat = selectBestFeatureToSplit(dataSet, i)
    # 获取最优属性特征
    bestFeatLabel = labels[bestFeat]
    # 将属性添加到featLables的末尾
    featLabels.append(bestFeatLabel)
    # 根据最优特征的标签生成树
    myTree = {bestFeatLabel: {}}
    # 删除已经使用特征标签
    del (labels[bestFeat])
    # 得到训练集中所有最优特征的属性值
    featValues = [example[bestFeat] for example in dataSet]
    # 去掉重复的属性值
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        # 递归调用函数createTree(),遍历特征，创建决策树。
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, featLabels, i)
    return myTree


# """
# 函数说明:使用决策树执行分类
# Parameters:
#     inputTree - 已经生成的决策树
#     featLabels - 存储选择的最优特征标签
#     testVec - 测试数据列表，顺序对应最优特征标签
# Returns:
#     classLabel - 分类结果
# """

# # 使用决策树执行分类
# def classify(inputTree, featLabels, testVec):
#     firstStr = next(iter(inputTree))  # 获取决策树结点
#     secondDict = inputTree[firstStr]  # 下一个字典
#     featIndex = featLabels.index(firstStr)
#     for key in secondDict.keys():
#         if testVec[featIndex] == key:
#             if type(secondDict[key]).__name__ == 'dict':
#                 classLabel = classify(secondDict[key], featLabels, testVec)
#             else:
#                 classLabel = secondDict[key]
#     return classLabel


if __name__ == '__main__':
    dataSet, labels = createDataSet()
    featLabels = []
    i = 0
    myTree = createTree(dataSet, labels, featLabels, i)
    print(myTree)
    visual_decision_tree.createPlot(myTree)
    # testVec = ['乌黑', '稍蜷', '浊响', '清晰', '稍凹', '软粘']  # 测试数据
    # result = classify(myTree, featLabels, testVec)
    # if result == '好瓜':
    #     print('好瓜')
    # if result == '坏瓜':
    #     print('坏瓜')

2、可视化决策树代码visual_decision_tree.py

import matplotlib.pylab as plt
import matplotlib

# 能够显示中文
matplotlib.rcParams['font.sans-serif'] = ['SimHei']
matplotlib.rcParams['font.serif'] = ['SimHei']

# 分叉节点，也就是决策节点
decisionNode = dict(boxstyle="sawtooth", fc="0.8")

# 叶子节点
leafNode = dict(boxstyle="round4", fc="0.8")

# 箭头样式
arrow_args = dict(arrowstyle="<-")


def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    """
    绘制一个节点
    :param nodeTxt: 描述该节点的文本信息
    :param centerPt: 文本的坐标
    :param parentPt: 点的坐标，这里也是指父节点的坐标
    :param nodeType: 节点类型,分为叶子节点和决策节点
    :return:
    """
    createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction',
                            xytext=centerPt, textcoords='axes fraction',
                            va="center", ha="center", bbox=nodeType, arrowprops=arrow_args)


def getNumLeafs(myTree):
    """
    获取叶节点的数目
    :param myTree:
    :return:
    """
    # 统计叶子节点的总数
    numLeafs = 0

    # 得到当前第一个key，也就是根节点
    firstStr = list(myTree.keys())[0]

    # 得到第一个key对应的内容
    secondDict = myTree[firstStr]

    # 递归遍历叶子节点
    for key in secondDict.keys():
        # 如果key对应的是一个字典，就递归调用
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        # 不是的话，说明此时是一个叶子节点
        else:
            numLeafs += 1
    return numLeafs


def getTreeDepth(myTree):
    """
    得到数的深度层数
    :param myTree:
    :return:
    """
    # 用来保存最大层数
    maxDepth = 0

    # 得到根节点
    firstStr = list(myTree.keys())[0]

    # 得到key对应的内容
    secondDic = myTree[firstStr]

    # 遍历所有子节点
    for key in secondDic.keys():
        # 如果该节点是字典，就递归调用
        if type(secondDic[key]).__name__ == 'dict':
            # 子节点的深度加1
            thisDepth = 1 + getTreeDepth(secondDic[key])

        # 说明此时是叶子节点
        else:
            thisDepth = 1

        # 替换最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth

    return maxDepth


def plotMidText(cntrPt, parentPt, txtString):
    """
    计算出父节点和子节点的中间位置，填充信息
    :param cntrPt: 子节点坐标
    :param parentPt: 父节点坐标
    :param txtString: 填充的文本信息
    :return:
    """
    # 计算x轴的中间位置
    xMid = (parentPt[0] - cntrPt[0]) / 2.0 + cntrPt[0]
    # 计算y轴的中间位置
    yMid = (parentPt[1] - cntrPt[1]) / 2.0 + cntrPt[1]
    # 进行绘制
    createPlot.ax1.text(xMid, yMid, txtString)


def plotTree(myTree, parentPt, nodeTxt):
    """
    绘制出树的所有节点，递归绘制
    :param myTree: 树
    :param parentPt: 父节点的坐标
    :param nodeTxt: 节点的文本信息
    :return:
    """
    # 计算叶子节点数
    numLeafs = getNumLeafs(myTree=myTree)

    # 计算树的深度
    depth = getTreeDepth(myTree=myTree)

    # 得到根节点的信息内容
    firstStr = list(myTree.keys())[0]

    # 计算出当前根节点在所有子节点的中间坐标,也就是当前x轴的偏移量加上计算出来的根节点的中心位置作为x轴（比如说第一次：初始的x偏移量为：-1/2W,计算出来的根节点中心位置为：(1+W)/2W，相加得到：1/2），当前y轴偏移量作为y轴
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.yOff)

    # 绘制该节点与父节点的联系
    plotMidText(cntrPt, parentPt, nodeTxt)

    # 绘制该节点
    plotNode(firstStr, cntrPt, parentPt, decisionNode)

    # 得到当前根节点对应的子树
    secondDict = myTree[firstStr]

    # 计算出新的y轴偏移量，向下移动1/D，也就是下一层的绘制y轴
    plotTree.yOff = plotTree.yOff - 1.0 / plotTree.totalD

    # 循环遍历所有的key
    for key in secondDict.keys():
        # 如果当前的key是字典的话，代表还有子树，则递归遍历
        if isinstance(secondDict[key], dict):
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            # 计算新的x轴偏移量，也就是下个叶子绘制的x轴坐标向右移动了1/W
            plotTree.xOff = plotTree.xOff + 1.0 / plotTree.totalW
            # 打开注释可以观察叶子节点的坐标变化
            # print((plotTree.xOff, plotTree.yOff), secondDict[key])
            # 绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff, plotTree.yOff), cntrPt, leafNode)
            # 绘制叶子节点和父节点的中间连线内容
            plotMidText((plotTree.xOff, plotTree.yOff), cntrPt, str(key))

    # 返回递归之前，需要将y轴的偏移量增加，向上移动1/D，也就是返回去绘制上一层的y轴
    plotTree.yOff = plotTree.yOff + 1.0 / plotTree.totalD


def createPlot(inTree):
    """
    需要绘制的决策树
    :param inTree: 决策树字典
    :return:
    """
    # 创建一个图像
    fig = plt.figure(1, facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)
    # 计算出决策树的总宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    # 计算出决策树的总深度
    plotTree.totalD = float(getTreeDepth(inTree))
    # 初始的x轴偏移量，也就是-1/2W，每次向右移动1/W，也就是第一个叶子节点绘制的x坐标为：1/2W，第二个：3/2W，第三个：5/2W，最后一个：(W-1)/2W
    plotTree.xOff = -0.5 / plotTree.totalW
    # 初始的y轴偏移量，每次向下或者向上移动1/D
    plotTree.yOff = 1.0
    # 调用函数进行绘制节点图像
    plotTree(inTree, (0.5, 1.0), '')
    # 绘制
    plt.show()