退火算法(SA)
1.是什么?为什么?怎么做?
Q1:模拟退火是什么算法?
模拟退火是模拟物理上退火方法,通过N次迭代(退火),逼近函数的上的一个最值(最大或者最小值)。
比如逼近这个函数的最大值C点:

Q2:模拟退火为什么可行?
讨论这个问题需要理解一下物理原型是怎么样的,也就是原来是怎么“退火”的:
模拟退火算法的思想借鉴于固体的退火原理,当固体的温度很高的时候,内能比较大,固体的内部粒子处于快速无序运动,当温度慢慢降低的过程中,固体的内能减小,粒子的慢慢趋于有序,最终,当固体处于常温时,内能达到最小,此时,粒子最为稳定。
注意标粗字体:
- 温度高->运动速度快(温度低->运动速度慢)
- 温度是缓慢(想象成特别慢的那种)降低的
- 温度基本不再变化后,趋于有序(最后内能达到最小,也就是接近最优)
我们通过模拟这个操作,使得我们需要的答案“趋于有序”,也就是最靠近需要的值(最值)。
Q3:怎么做?
大方向
首先,理解一下大方向:
模拟退火就是一种循环算法。
- 我们先设定一个初始的温度 T T T(这个温度会比较高,比如2000)
- 每次循环都退火一次。(具体怎么操作后面详解)
- 然后降低 T T T的温度,我们通过让 T T T和一个“降温系数” Δ T \Delta T ΔT(一个接近1的小数,比如 0.99 0.99 0.99)相乘,达到慢慢降低温度的效果,直到接近于0(我们用 e p s eps eps来代表一个接近0的数(比如0.00001),只要 T < e p s T<eps T<eps就可以退出循环了)
所以总的来说,用伪代码表示退火的流程是这样的:
double T = 2000; //代表开始的温度
double dT = 0.99; //代表系数delta T
double eps = 1e-14; //相当于0.0000000000000001
while(T > eps) {
//--------------
//这里是每一次退火的操作
//--------------
T = T * dT; //温度每次下降一点点, T * 0.99
}
退火详解
我们要求解的答案无非是两个:自变量 x x x和对应函数的最大值f(x)
那么模拟退火的是怎么做到的呢?
-
我们先随机找一点 x 0 x_0 x0 ,不论是哪个点都可以,随机!(不超过定义域就行)。
这个点作为我们的初始值(相当于物体里的一个粒子)

2.再找到一点 f ( x 0 ) f(x_0) f(x0),来代表 x 0 x_0 x0所对应的函数值

3.现在正式开始退火!
刚才我们说了 x 0 x_0 x0相当于是一个粒子,所以我们会进行一个无序运动,也就是向左或者向右随机移动
是的,是随机移动,可能向左,也可能向右,但是请记住一个关键点:移动的幅度和当前的温度T有关。
**温度 T T T越大,移动的幅度越大。温度 T T T越小,移动的幅度就越小。**这是在模拟粒子无序运动的状态。
4.接受(Accept)更"好"的状态

假设我们移动到了 x 1 x_1 x1处,那么这个点对应的 f ( x 1 ) f(x_1) f(x1)很明显答案是优于(大于)当前的 f ( x 0 ) f(x_0) f(x0)的

因此我们将答案进行更新。也就是将初始值进行替换: x 0 = x 1 , f ( x 0 ) = f ( x 1 ) x_0=x_1,f(x_0)=f(x_1) x0=x1,f(x0)=f(x1)。这是一种贪心的思想。
5.以一定概率接受(Accept)更差的状态
这是退火最精彩的部分。
为什么我们要接受一个更加差的状态呢?因为可能在一个较差的状态旁边会出现一个更加高的山峰

如果我们鼠目寸光,只盯着右半区,很容易随着温度的下降、左右跳转幅度的减小而迷失自己,最后困死在小山丘中。
而我们如果找到了左边山峰的低点,以一定的概率接受了它(概率大小和温度以及当前的值的关键程度有关),会在跳转幅度减少之前,尽可能找到最优点。
那么我们以多少的概率去接受它呢?我们用一个公式表示(这个公式我们只需记住,这是科学家推导出来的结论): e Δ f k T \Huge e^{\frac{\Delta f}{kT}} ekTΔf 别慌!很简单!我们来理解一下这里面的变量:
- e是自然对数,约等于2.71。我们可以把右上角这一坨值 Δ f k T \frac{\Delta f}{kT} kTΔf看成一个整体 x x x:
ex的图形画出来是这样的:

因为我们想要函数 e x e^x ex来代表一个概率值,所以我们只需要关注x为负数的部分即可:
负数部分的值域是在 ( 0 , 1 ) (0,1) (0,1)开区间内,x越小,越接近0,越大越靠近1。
因为在0到1之间,所以这个值相当于是概率了。比如 e x = 0.97 e^x=0.97 ex=0.97,那么我们接受的概率就是 97 97% 97
而正数部分的值域会大于1,也就是说概率会超过 100 100% 100,所以会一定选(其实是上一种找到更优的情况)
- k T kT kT
k k k其实是个物理学常数,我们在代码中不会用到。
T T T很简单,就是当前的温度。所以实际上这个分母就是 T T T, k k k当做 1 1 1使用。
-
Δ f \Delta f Δf
我们着重讲一下什么是 Δ f \Delta f Δf。
其实从前面的函数 e x e^x ex中可以发现, Δ f \Delta f Δf必须是个负数!
我们想要函数 e x e^x ex来代表一个概率值,一定要让它的值域属于 ( 0 , 1 ) (0,1) (0,1),所以 Δ f k T \frac{\Delta f}{kT} kTΔf必须是个负数。但是 k T kT kT在我们的模拟中一定是正数,那么 Δ f \Delta f Δf必须是个负数!
其实 Δ f \Delta f Δf就是当前解的函数值与目标解函数值之差,$\Delta f= - \left | f(x_0)-f(x_1) \right | $,并且一定是个负数。这个需要具体问题具体分析。
比如现在我们求一个函数的最大值,那么如果 f ( x 0 ) < f ( x 1 ) f(x_0) < f(x_1) f(x0)<f(x1)了,那就说明结果变好了,我们肯定选择它(见第4点)
如果 f ( x 0 ) > f ( x 1 ) f(x_0) > f(x_1) f(x0)>f(x1),那就说明结果变差了,我们需要概率选择它,因此 Δ f = − ( f ( x 0 ) − f ( x 1 ) ) \Delta f=-(f(x_0) - f(x_1)) Δf=−(f(x0)−f(x1))

所以总结一下就是:
- 随机后的函数值如果结果更好,我们一定选择它(即 x 0 = x 1 , f ( x 0 ) = f ( x 1 ) x_0=x_1,f(x_0)=f(x_1) x0=x1,f(x0)=f(x1))
- 随机后的函数值如果结果更差,我们以 e Δ f k T \LARGE e^{\frac{\Delta f}{kT}} ekTΔf的概率接受它
注:对代码中的函数作出解释:
①对rand()函数
- rand()函数可以默认拿到[0,32767]内的随机整数
- RAND_MAX = 32767,可以看作常量。本质是宏定义: #define RAND_MAX 32767
- rand() * 2 的范围是[0,32767 * 2]
- rand() * 2 - RAND_MAX 的范围是[-32767, 32767]
②对exp()函数
- exp(x)代表 e x e^x ex
③关于exp((df - f) / T) * RAND_MAX > rand()
- 目的是要概率接受,但是 e x e^x ex是个准确值,所以从理论上我们可以生成一个(0,1)的随机数,如果 e x e^x ex比(0,1)这个随机数要大,那么我们就接受。
- 但是由于rand()只能产生[0,32767]内的随机整数,化成小数太过麻烦。所以我们可以把左边乘以RAND_MAX(也就是把概率同时扩大32767倍),效果就等同于 e x e^x ex比(0,1)了。
double T = 2000; //代表开始的温度
double dT = 0.99; //代表系数delta T
double eps = 1e-14; //相当于0.0000000000000001
//用自变量计算函数值,这里可能存在多个自变量对应一个函数值的情况,比如f(x,y)
double func(int x, ... ) {
//这里是对函数值进行计算
double ans = .......
return ans;
}
//原始值
double x = rand(); //x0取随机值
double f = func(x,...); //通过自变量算出f(x0)的值
while(T > eps) {
//--------------
//这里是每一次退火的操作
//x1可以左右随机移动,幅度和温度T正相关,所以*T
//注意这里移动可以左右移动,但是也可以单向移动
//关于rand()详细见开头注的①
double dx = (2*rand() - RAND_MAX) * T;
//让x落在定义域内,如果没在里面,就重新随机。题目有要求需要写,否则不用写
// ================
while(x > ? || x < ? ...) {
double dx = (2*rand() - RAND_MAX) * T;
}
// ================
//求出f(x1)的值
double df = func(dx);
//这里需要具体问题具体分析,我们要接受更加优秀的情况。可能是df < f(比如求最小值)
if(f < df) {
f = df; x = dx; [...,y = dy;] // 接受,替换值,如果多个自变量,那么都替换
}
//否则概率接受,注意这里df-f也要具体问题具体分析。
//详细见开头注的②③
else if(exp((df - f) / T) * RAND_MAX > rand()) {
f = df; x = dx; [...y = dy;] // 接受,替换值,如果多个自变量,那么都替换
}
//--------------
T = T * dT; //温度每次下降一点点, T * 0.99
}
//最后输出靠近最优的自变量x值,和函数值f(x)
cout << x << " " << f << endl;
2.通过模拟退火算出 n \sqrt{n} n 的值
思路是这样的:我们试图通过退火找出一个值 x 0 x_0 x0,使得 x 0 2 {x_0}^2 x02的值更加接近于 n 2 {\sqrt{n}}^2 n2。(记住退火是让一个随机值去逼近最后的答案)
因为 x 0 2 {x_0}^2 x02的值更加接近于 n 2 {\sqrt{n}}^2 n2。因此 x 0 x_0 x0值就更加接近于 n \sqrt{n} n
-
所以我们需要一个函数 f ( x ) f(x) f(x),算出 x 0 2 {x_0}^2 x02和 n 2 {\sqrt{n}}^2 n2的接近程度,那么毋庸置疑,我们需要算出他们绝对值的差。 f ( x ) = ∣ x 2 − n ∣ f(x)=\left |x^2 - n \right | f(x)= x2−n 也就是说我们的函数表达式就有了
//n代表我们最后函数要逼近的值 double n; //x表示我们随机产生的那个数的平方和n的靠近程度 double func(double x) { return fabs(x * x - n); } -
写出退火函数SA()
double T = 20000; //初始温度,初始温度主要是看题目开始需要跳转的幅度。 double dT = 0.993; //变化率,这里需要速度稍微慢一点,写0.995 或者 0.997都可以,但是越靠近1速度就越慢 const double eps = 1e-14; //10的-14次方已经非常小了,写这个大概率没问题 void SA() { //首先随机生成一个点x0,这里我用0代替。 double x = 0; //算出x平方和n的差距f(x0) double f = func(x); while(T > eps) { //这里x0既可以变小,也可以变大,所以我们正负都要进行一个跳转,算出变换后的点dx double dx = x + (2 * rand() - RAND_MAX) * T; //但是请注意,dx很明显要保证 >= 0才行,因为算术平方根的定义域是>=0,因此小于0就重新随机 while(dx < 0) dx = x + (2 * rand() - RAND_MAX) * T; //算出变换后的点dx的平方和n的差距,f(dx) double df = func(dx); //这里就是关键的地方了,很明显我们需要算出来的function值越小,自变量x更加接近那个根号值。 //所以如果新来的值df 比 f更小,我们百分百接受 if(df < f) { //注意更新所有变量 f = df; x = dx; } //否则我们概率接受,这里的需要写 f - df了,因为这样才是负值。负值说明我们并不是贪心接受的,他是不太好的值。 else if(exp((f - df)/T) * RAND_MAX > rand()) { //注意更新所有变量 f = df; x = dx; } //温度下降一下 T *= dT; } printf("%.8lf",x); }
最后贴上完整代码和注释供大家调试。
#include <bits/stdc++.h>
using namespace std;
//n代表我们最后函数要逼近的值
double n;
//x表示我们随机产生的那个数的平方和n的靠近程度
double func(double x) {
return fabs(x * x - n);
}
double T = 20000; //初始温度,初始温度主要是看题目开始需要跳转的幅度。
double dT = 0.993; //变化率,这里需要速度稍微慢一点,写0.995 或者 0.997都可以,但是越靠近1速度就越慢
const double eps = 1e-14; //10的-14次方已经非常小了,写这个大概率没问题
void SA() {
//首先随机生成一个点x0,这里我用0代替。
double x = 0;
//算出x平方和n的差距f(x0)
double f = func(x);
while(T > eps) {
//这里x0既可以变小,也可以变大,所以我们正负都要进行一个跳转,算出变换后的点dx
double dx = x + (2 * rand() - RAND_MAX) * T;
//但是请注意,dx很明显要保证 >= 0才行,因为算术平方根的定义域是>=0,因此小于0就重新随机
while(dx < 0) dx = x + (2 * rand() - RAND_MAX) * T;
//算出变换后的点dx的平方和n的差距,f(dx)
double df = func(dx);
//这里就是关键的地方了,很明显我们需要算出来的function值越小,自变量x更加接近那个根号值。
//所以如果新来的值df 比 f更小,我们百分百接受
if(df < f) {
//注意更新所有变量
f = df; x = dx;
}
//否则我们概率接受,这里的需要写 f - df了,因为这样才是负值。负值说明我们并不是贪心接受的,他是不太好的值。
else if(exp((f - df)/T) * RAND_MAX > rand()) {
//注意更新所有变量
f = df; x = dx;
}
//温度下降一下
T *= dT;
}
printf("%.8lf",x);
}
int main()
{
cin >> n;
SA();
}
遗传算法(GA)
什么是遗传算法?
模拟大自然中,种群在选择压力下的演化(物竞天择、适者生存),从而得到问题的一个近似解。在计算机中模拟自然中基因与进化的关系,用于解决优化问题。
算法特点
- 良好的并行性(操作对象是一组可行解;搜索轨道有多条)
- 强大的通用性(只需利用目标的取值信息,无需梯度等高价作信息)
- 良好的全局优化性和鲁棒性
- 良好的可操作性
两个缺点:
- 收敛速度慢
- 算法实时性欠佳
遗传算法的应用领域
- 函数优化(经典应用)求解函数的最优解
- 组合优化(旅行商问题——已成为衡量算法优劣的标准、背包问题装箱问题等)设计方案的问题
- 生产调度问题
- 自动控制(如航空控制系统的优化设计、模糊控制器优化设计和在线修改隶属度函数、人工神经网络结构优化设计和调整人工神经网络的连接权等优化问题)
- 机器人智能控制(如移动机器人路径规划、关节机器人运动轨迹规划机器人逆运动学求解等)
- 图像处理和模式识别(如图像恢复、图像边缘特征提取、几何形状识别等)
- 机器学习(将GA用于知识获取,构建基于GA的机器学习系统)
相关术语
| 基因型: | 性状染色体的内部表现; |
|---|---|
| 表现型: | 染色体决定的性状的外部表现,或者说,根据基因型形成的个体的外部表现; |
| 进化: | 种群逐渐适应生存环境,品质不断得到改良。生物的进化是以种群的形式进行的。 |
| 适应度: | 度量某个物种对于生存环境的适应程度。 |
| 选择: | 以一定的概率从种群中选择若干个个体。一般,选择过程是一种基于适应度的优胜劣汰的过程。 |
| 复制: | 细胞分裂时,遗传物质DNA通过复制而转移到新产生的细胞中,新细胞就继承了旧细胞的基因。 |
| 交叉: | 两个染色体的某一相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染色体。也称基因重组或杂交; |
| 变异: | 复制时可能(很小的概率)产生某些复制差错,变异产生新的染色体,表现出新的性状。 |
| 编码: | DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。 |
前言
对于遗传算法的关键,就在于基因型和表现型的映射关系,即,什么样的基因,就有什么样的表现型,而基因是根据染色体来表现的,同时,我们在解决问题的时候是根据其表现性来判断其优劣性的。
遗传算法中每一条染色体,对应着遗传算法的一个解决方案,一般我们用适应性函数(fitness function)来衡量这个解决方案的优劣。所以从一个基因组到其解的适应度形成一个映射。可以把遗传算法的过程看作是一个在多元函数里面求最优解的过程。 可以这样想象,这个多维曲面里面有数不清的“山峰”,而这些山峰所对应的就是局部最优解。而其中也会有一个“山峰”的海拔最高的,那么这个就是全局最优解。而遗传算法的任务就是尽量爬到最高峰,而不是陷落在一些小山峰。(另外,值得注意的是遗传算法不一定要找“最高的山峰”,如果问题的适应度评价越小越好的话,那么全局最优解就是函数的最小值,对应的,遗传算法所要找的就是“最深的谷底”)
那么遗传算法和退火算法的不同之处在于:退火算法是以点为单位的搜索,而遗传算法是以面为单位的搜索。
示例:“袋鼠跳”问题
已知一元函数: f ( x ) = x sin ( 10 π x ) + 2 x ∈ [ − 1 , 2 ] f(x)=x \sin (10 \pi x)+2 \quad x \in[-1,2] f(x)=xsin(10πx)+2x∈[−1,2],现在要求在既定的区间内找出函数的最大值
既然我们把函数曲线理解成一个一个山峰和山谷组成的山脉。那么我们可以设想所得到的每一个解就是一只袋鼠,我们希望它们不断的向着更高处跳去,直到跳到最高的山峰(尽管袋鼠本身不见得愿意那么做)。所以求最大值的过程就转化成一个“袋鼠跳”的过程。
模拟物竞天择的生物进化过程,通过维护一个潜在解的群体执行了多方向的搜索,并支持这些方向上的信息构成和交换。是以面为单位的搜索,比以点为单位的搜索,更能发现全局最优解。(在遗传算法中,有很多袋鼠,它们降落到喜玛拉雅山脉的任意地方。这些袋鼠并不知道它们的任务是寻找珠穆朗玛峰。但每过几年,就在一些海拔高度较低的地方射杀一些袋鼠,并希望存活下来的袋鼠是多产的,在它们所处的地方生儿育女。)(或者换个说法。从前,有一大群袋鼠,它们被莫名其妙的零散地遗弃于喜马拉雅山脉。于是只好在那里艰苦的生活。海拔低的地方弥漫着一种无色无味的毒气,海拔越高毒气越稀薄。可是可怜的袋鼠们对此全然不觉,还是习惯于活蹦乱跳。于是,不断有袋鼠死于海拔较低的地方,而越是在海拔高的袋鼠越是能活得更久,也越有机会生儿育女。就这样经过许多年,这些袋鼠们竟然都不自觉地聚拢到了一个个的山峰上,可是在所有的袋鼠中,只有聚拢到珠穆朗玛峰的袋鼠被带回了美丽的澳洲。)
遗传算法的实现过程
遗传算法的实现过程实际上就像自然界的进化过程那样。首先寻找一种对问题潜在解进行“数字化”编码的方案。(建立表现型和基因型的映射关系)然后用随机数初始化一个种群(那么第一批袋鼠就被随意地分散在山脉上),种群里面的个体就是这些数字化的编码。接下来,通过适当的解码过程之后(得到袋鼠的位置坐标),用适应性函数对每一个基因个体作一次适应度评估(袋鼠爬得越高,越是受我们的喜爱,所以适应度相应越高)。用选择函数按照某种规定择优选择(我们要每隔一段时间,在山上射杀一些所在海拔较低的袋鼠,以保证袋鼠总体数目持平。)。让个体基因变异(让袋鼠随机地跳一跳)。然后产生子代(希望存活下来的袋鼠是多产的,并在那里生儿育女)。遗传算法并不保证你能获得问题的最优解,但是使用遗传算法的最大优点在于你不必去了解和操心如何去“找”最优解。(你不必去指导袋鼠向那边跳,跳多远。)而只要简单的“否定”一些表现不好的个体就行了。(把那些总是爱走下坡路的袋鼠射杀,这就是遗传算法的精粹!)
所以我们总结出遗传算法的一般步骤:
开始循环直至找到满意的解。
1.评估每条染色体所对应个体的适应度。
2.遵照适应度越高,选择概率越大的原则,从种群中选择两个个体作为父方和母方。
3.抽取父母双方的染色体,进行交叉,产生子代。
4.对子代的染色体进行变异。
5.重复2,3,4步骤,直到新种群的产生。
结束循环。
编制袋鼠的染色体----基因的编码方式
受到人类染色体结构的启发,我们可以设想一下,假设目前只有“0”,“1”两种碱基,我们也用一条链条把他们有序的串连在一起,因为每一个单位都能表现出 1 bit的信息量,所以一条足够长的染色体就能为我们勾勒出一个个体的所有特征。这就是二进制编码法,染色体大致如下:
010010011011011110111110
上面的编码方式虽然简单直观,但明显地,当个体特征比较复杂的时候,需要大量的编码才能精确地描述,相应的解码过程(类似于生物学中的DNA翻译过程,就是把基因型映射到表现型的过程。)将过分繁复,为改善遗传算法的计算复杂性、提高运算效率,提出了浮点数编码。染色体大致如下:
1.2 –3.3 – 2.0 –5.4 – 2.7 – 4.3
(注:还有一种编码方式叫符号编码)
那么我们如何利用这两种编码方式来为袋鼠的染色体编码呢?因为编码的目的是建立表现型到基因型的映射关系,而表现型一般就被理解为个体的特征。比如人的基因型是46条染色体所描述的却能解码成一个眼,耳,口,鼻等特征各不相同的活生生的人。所以我们要想为“袋鼠”的染色体编码,我们必须先来考虑“袋鼠”的“个体特征”是什么。也许有的人会说,袋鼠的特征很多,比如性别,身长,体重,也许它喜欢吃什么也能算作其中一个特征。但具体在解决这个问题的情况下,我们应该进一步思考:无论这只袋鼠是长短,肥瘦,黑白只要它在低海拔就会被射杀,同时也没有规定身长的袋鼠能跳得远一些,身短的袋鼠跳得近一些。当然它爱吃什么就更不相关了。**我们由始至终都只关心一件事情:袋鼠在哪里。**因为只要我们知道袋鼠在那里,我们就能做两件必须去做的事情:
(1)通过查阅喜玛拉雅山脉的地图来得知袋鼠所在的海拔高度(通过自变量求适应函数的值。)以判断我们有没必要把它射杀。
(2)知道袋鼠跳一跳(交叉和变异)后去到哪个新位置。
如果我们一时无法准确的判断哪些“个体特征”是必要的,哪些是非必要的,我们常常可以用到这样一种思维方式:比如你认为袋鼠的爱吃什么东西非常必要,那么你就想一想,有两只袋鼠,它们其它的个体特征完全同等的情况下,一只长得黑,另外一只长得不是那么黑。你会马上发现,这不会对它们的命运有丝毫的影响,它们应该有同等的概率被射杀!只因它们处于同一个地方。(值得一提的是,如果你的基因编码设计中包含了袋鼠黑不黑的信息,这其实不会影响到袋鼠的进化的过程,而那只攀到珠穆朗玛峰的袋鼠黑与白什么的也完全是随机的,但是它所在的位置却是非常确定的。)
以上是对遗传算法编码过程中经常经历的思维过程,必须把具体问题抽象成数学模型,突出主要矛盾,舍弃次要矛盾。只有这样才能简洁而有效的解决问题。
物竞天择--适应性评分与及选择函数。
1.物竞――适应度函数(fitness function)
自然界生物竞争过程往往包含两个方面:生物相互间的搏斗与及生物与客观环境的搏斗过程。但在我们这个实例里面,你可以想象到,袋鼠相互之间是非常友好的,它们并不需要互相搏斗以争取生存的权利。它们的生死存亡更多是取决于你的判断。因为你要衡量哪只袋鼠该杀,哪只袋鼠不该杀,所以你必须制定一个衡量的标准。而对于这个问题,这个衡量的标准比较容易制定:袋鼠所在的海拔高度。(因为你单纯地希望袋鼠爬得越高越好。)所以我们直接用袋鼠的海拔高度作为它们的适应性评分。即适应度函数直接返回函数值就行了。
2.天择――选择函数(selection)
自然界中,越适应的个体就越有可能繁殖后代。但是也不能说适应度越高的就肯定后代越多,只能是从概率上来说更多。(毕竟有些所处海拔高度较低的袋鼠很幸运,逃过了你的眼睛。)那么我们怎么来建立这种概率关系呢?下面我们介绍一种常用的选择方法――轮盘赌(Roulette Wheel Selection)选择法
比如我们有5条染色体,他们所对应的适应度评分分别为:5,7,10,13,15。
所以累计总适应度为: F = ∑ i = 1 n f i = 5 + 7 + 10 + 13 + 15 = 50 F=\sum_{i=1}^{n} f_{i}=5+7+10+13+15=50 F=∑i=1nfi=5+7+10+13+15=50
所以各个个体被选中的概率分别为:
P 1 = f 1 F × 100 % = 5 50 × 100 % = 10 % P 2 = f 2 F × 100 % = 7 50 × 100 % = 14 % P 3 = f 3 F × 100 % = 10 50 × 100 % = 20 % P 4 = f 4 F × 100 % = 13 50 × 100 % = 26 % P 5 = f 5 F × 100 % = 15 50 × 100 % = 30 % \begin{array}{l} P_{1}=\frac{f_{1}}{F} \times 100 \%=\frac{5}{50} \times 100 \%=10 \% \\ P_{2}=\frac{f_{2}}{F} \times 100 \%=\frac{7}{50} \times 100 \%=14 \% \\ P_{3}=\frac{f_{3}}{F} \times 100 \%=\frac{10}{50} \times 100 \%=20 \% \\ P_{4}=\frac{f_{4}}{F} \times 100 \%=\frac{13}{50} \times 100 \%=26 \% \\ P_{5}=\frac{f_{5}}{F} \times 100 \%=\frac{15}{50} \times 100 \%=30 \% \end{array} P1=Ff1×100%=505×100%=10%P2=Ff2×100%=507×100%=14%P3=Ff3×100%=5010×100%=20%P4=Ff4×100%=5013×100%=26%P5=Ff5×100%=5015×100%=30%
你可以想象一下,我们转动轮盘,轮盘停下来的时候,指针会随机地指向某一个个体所代表的区域,那么非常幸运地,这个个体被选中了。(很明显,适应度评分越高的个体被选中的概率越大。)
MATLAB中的应用
1.可以在APP中选择Optimization Tool即可使用
2.在命令行中输入optimtool(‘ga’) 即可使用
参考文章:http://t.csdn.cn/YsuCM http://t.csdn.cn/RqOYV http://t.csdn.cn/EhF5j http://t.csdn.cn/fVZUe
参考视频:https://www.bilibili.com/video/BV12r4y1k7Yf?share_source=copy_web&vd_source=279c39b25c6851e98f90ff6735e9044c
BP神经网络
值得注意的是,神经网络为neural network,而所谓的BP神经网络,那么BP,即是back propagation,反向传播,因此,BP神经网络即是具有反向传播的神经网络。
bp神经网络是一种按误差逆传播算法训练的多层前馈网络,是目前应用最广泛的神经网络模型之一。bp神经网络的学习规则是使用最速下降法,通过反向传播来不断调整网络的权值和阈值,使网络的分类错误率最小。
**神经网络的作用:**进行拟合或者进行预测(仿真)。
反向传播(BP)
什么是反向传播呢?
比如你的朋友买了一双鞋,让你猜价格。
你第一次猜99块钱,他说猜低了。
你第二次猜101块钱,他说猜高了。
你第三次猜100块钱,他说猜对了。
你猜价格的这个过程是利用随机的数据给出一个预测值,这是一个正向传播。
而你的朋友将你的预测值与真实值进行对比,然后给出一个评价,这个过程是一个反向传播。(反馈)
神经网络也是类似的过程,通过对网络的超参数进行随机配置,得到一个预测值。这是一个正向传播的过程。**而后计算出预测值与真实值的差距,根据这个差距相应的调整参数,这是一个反向传播的过程。**通过多次迭代,循环往复,我们就能计算出一组合适的参数,得到的网络模型就能拟合一个我们未知的复杂函数。
BP神经网络的示意图

其中蓝色的箭头是正向传播的过程,黄色的线条就是反向传播。
BP神经网络的具体描述

上面这张图是BP神经网络的拓扑结构。简而言之就是分为三个“层”。输入层、隐藏层和输出层(一般情况下隐藏层会有若干层,这里只画了一个隐藏层)。每个层都包含若干个神经元(图中圆形)。上一层的输出作为下一层输入(数据的联系如图中连线所示)
单个神经元

单个的神经元如上图所示。其中, x i x_{i} xi为输入, w i w_{i} wi为输出, θ i θ_{i} θi代表阈值, y k y_{k} yk代表输出。这里还有一个偏置 b b b和激活函数 f ( x ) f(x) f(x)没有画出。总之,一个神经元需要四个参数和一个函数才能得到输出(输入、权重、阈值、偏置还有激活函数)
激活函数
Sigmoid ( x ) = 1 1 + e − x \operatorname{Sigmoid}(x)=\frac{1}{1+e^{-x}} Sigmoid(x)=1+e−x1
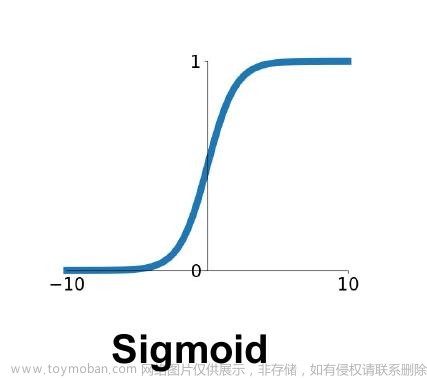
tanh
(
x
)
=
1
−
e
−
2
x
1
+
e
−
2
x
=
2
(
1
1
+
e
−
2
x
)
−
1
=
2
sigmoid
(
2
x
)
−
1
\tanh (x)=\frac{1-e^{-2 x}}{1+e^{-2 x}}=2\left(\frac{1}{1+e^{-2 x}}\right)-1=2 \operatorname{sigmoid}(2 x)-1
tanh(x)=1+e−2x1−e−2x=2(1+e−2x1)−1=2sigmoid(2x)−1
f
(
x
)
=
max
(
0
,
x
)
f(x)=\max (0, x)
f(x)=max(0,x)
RELU函数
对于隐藏层的激活函数,必须为非线性函数,因为线性函数的组合本身就是线性函数,所以除非引入非线性,否则无法计算更复杂的函数,即使网络层数再多也不行。
激活函数的种类:relu激活函数,sigmoid激活函数,tanh激活函数等。
对于隐藏层一般使用relu激活函数,对于输出层如果用于分类则采用sigmoid激活函数,用于回归则采用线性激活函数。
对于损失函数,涉及到数学,不作讨论。
对于MATLAB的BP神经网络,参考文章很详细,不再赘述。
参考文章:http://t.csdn.cn/a9DAb
灰色关联度分析与灰色预测
参考文章:http://t.csdn.cn/RFOFV
对于灰色系统,我们主要建立了两种数学模型:灰色关联度分析与灰色预测。
灰色关联度分析
对于灰色关联度分析,实际上就是对于某一组数据,判断其中一者与其他数据的关联性。
对于这种关联度的分析,其最大的特点是:所用的数据较少(相较于回归分析是一个优点),最少4组数据就可以进行分析。数据的类型可以是离散的。
在计算过程中,我们需要对于数据进行无量纲化处理,因为在实际问题里,不同的数据之间量纲是不统一的,因此要首先进行数据变换。
灰色预测
灰色预测是指利用GM模型对系统行为特征的发展变化规律进行估计预测。主要以灰色系统理论中的GM(1,1)模型来进行处理。文章来源:https://www.toymoban.com/news/detail-718200.html
GM(1,1)即表示模型是 1 阶的,且只含 1 个变量的灰色模型。而GM(1, N) 即表示 模型是 1 阶的,包含有 N 个变量的灰色模型。文章来源地址https://www.toymoban.com/news/detail-718200.html
到了这里,关于数学建模部分算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!











