1.矩阵
1.矩阵运算符
| 运算 | 符号 | 说明 | 具体表现实现 |
|---|---|---|---|
| 转置 | A.' | 矩阵转置 | 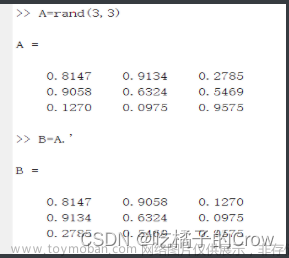 |
| 共轭转置 | A' | 复矩阵共轭转置,当A为实数矩阵时等价于A.' |  |
| 加减 | A+B、A-B | 矩阵元素之间相互进行加减 |  |
| 数与矩阵加减 | K+A、K-A | 数与矩阵的加减操作 |  |
| 数乘以矩阵 | k*A | 数对矩阵中的每个元素进行相乘 |  |
| 矩阵相乘 | A * B A.*B | 乘法运算:点乘(对应元素相乘) 乘(矩阵相乘) |  |
| 矩阵乘方 | A^k | 相当于k个A进行相乘 |  |
| 矩阵除法 | 左除A\B 右除A/B | 相当于AX=B XA=B的解 |  |
2.特殊矩阵的生成
1.零矩阵
-
zeros(m,n) 生成m行n列的零矩阵
2. 1矩阵
-
ones(m,n)生成m行n列元素都为1的矩阵

3.单位阵
-
eye(n) 生成n阶单位阵

4.随机矩阵
-
rand(m,n) 生成m行n列在[0,1]上均匀分布的随机矩阵

3.矩阵处理

1.矩阵的迹(对角线之和)
-
trace(A) 返回矩阵A的迹(对角线元素的和)

2.提取对角线向量
-
diag(A) 返回矩阵A的对角线元素构成的向量

3.向量生成的对角矩阵
-
diag(x) 返回由向量x的元素构成的对角矩阵

4.提取下三角矩阵
-
tril(A) 提取矩阵A的下三角矩阵

5.提取上三角矩阵
-
triu(A) 提取矩阵A的上三角矩阵

6.矩阵上下翻转
-
flipud(A) 矩阵上下翻转

7.矩阵左右翻转
-
fliplr(A) 矩阵左右翻转

8.重排矩阵
-
reshape(A,m,n) 将矩阵A的元素重排成m行n列矩阵

4.矩阵分析

1.rank(矩阵的秩运算)
-
rank(A) 返回A的秩

2.det(矩阵的行列式运算)
-
det(A) 返回方阵A的行列式

3.inv(矩阵的逆运算)
-
inv(A) 返回A的逆矩阵

4.null(AX=0的基础解系)
-
null(A) 返回A的零矩阵的基,即AX=0的基础解系

5.orth(矩阵的正交规范基)
-
orth(A) 求A的列向量空间的正交规范基

6.norm(向量的范数)x
-
norm(x) 返回向量x的范数(向量“大小”的度量),即

7.norm(矩阵的范数)A
-
norm(A) 返回矩阵A的范数(矩阵“大小”的度量),即


8.expm(矩阵的指数函数)
-
expm(A) 返回矩阵A的指数函数,即级数和


9.矩阵的特征值以及特征向量
-
[V,D]=eig(A) V--特征向量矩阵 D--特征值的对角矩阵

10.magic(幻方矩阵)
例题:秩对解的影响
用矩阵除法解下列线性方程组,并判断解的意义,用矩阵乘方进行验算
-
如果rank(A,b)==rank(A)---->方程有解
-
rank(A)==length(A) 有唯一解 (满秩)----> 可逆 <--det(A)!=0
-
rank(A)<length(A) 有无穷多解 det(A)==0---->不可逆
-
-
rank(A)<rank(A,b)---->方程无解
if rank(A)==rank([A,b])
disp("方程组有解");
%使用rref求出矩阵的最简形式(行简化阶梯型)
simple=rref([A,b])
if rank(A)==length(A)
disp("方程组有唯一解");
else if rank(A)<length(A)
disp("方程组有无穷多解");
end
end
else
disp("方程组无解");
end
2.函数与图像
1.基本语句
1.if条件控制语句
if 情况1(满足情况1则会执行结果1)
结果1
else(否则就会执行结果2)
结果2
endif 情况1(满足情况1则会执行结果1)
结果1
else if 情况2(满足情况2则会执行结果2)
结果2
else(否则执行结果3)
结果3
end
2.switch选择语句
switch a(与a相比,若相同则执行对应的结果)
case a1
结果1
case a2
结果2
case a3
结果3
...
otherwise
结果n
end3.try-catch语句
try
%可能会抛出异常的代码
catch
%处理异常代码
end4.for循环
for index=起始点:终点值
循环操作
end5.while循环
while 循环条件
循环操作
end2.函数
1.函数的定义
function 返回的结果参数=函数名(入参)
函数实际操作
end
function sum=func1(n)
if n<1
sum=1;
else
sum=func1(n-1)*n;
end2.函数的运行
result=func1(5) //定义一个变量去接收结果3.绘制图像
1.曲线图 曲面图
sin(x)
>> x=0:0.01:2*pi;//设置x区间步长
>> y=sin(x);//设置需要画图的函数
>> plot(x,y);//画图
>> xlabel("x轴");//设置x轴名称
>> ylabel("y轴");//设置y轴名称
>> title("sin(x)")//设置标题常用颜色以及线型
颜色:
‘b’ - 蓝色(blue)
‘g’ - 绿色(green)
'r' - 红色(red)
'c' - 青色 (cyan)
'm' - 洋红色(magenta)
'y' - 黄色(yellow)
'k' - 黑色(black)
'w' - 白色(white)
线型:
‘-’ 实线(solid)
'--' 虚线(dashed)
':' 点线(dotted)
'-.' 点划线(dash-dotted)
x=0:0.01:2*pi;//设置x区间步长
y=sin(x);//设置需要画图的函数
plot(x,y,'r--');//画图
xlabel("x轴");//设置x轴名称
ylabel("y轴");//设置y轴名称
title("sin(x)")//设置标题
legrnd('sin(x)')//设置图例ezplot(可迅速绘制简单图形)
ezplot('sin(x)',[0,2*pi])

stairs(阶梯状曲线图)
stairs(x,y,'LineWidth',2)

x=randn(1,100);
x=randn(1,100);
>> y=randn(1,100);
>> scatter(x,y,"filled")
poparplot(绘制极坐标图)
>> x=linspace(0,2*pi,100);
>> y=2*sin(3*x);
>> polarplot(x,y,"LineWidth",2)
area(绘制面积图,数据之前的关系变化趋势)
x=0:0.1:2*pi;
>> y1=sin(x);
>> y2=cos(x);
>> area(x,[y1:y2]','LineStyle','--')
contour(绘制等高线)
[X,Y]=meshgrid(-2:0.1:2);
>> Z=X.^2+Y.^2;
>> contour(X,Y,Z,20)
quiver(绘制矢量图,向量的大小以及方向)
[X,Y]=meshgrid(-2:0.1:2);
>> Z=X.^2+Y.^2;
>> contour(X,Y,Z,20)
>> [DX,DY]=gradient(Z,0.25,0.25);
>> quiver(X,Y,DX,DY)
surf(绘制三维曲面图,三元函数的空间形态)
[X,Y]=meshgrid(-2:0.1:2);
Z=peaks(X,Y);
surf(x,y,z)
histogram(绘制直方图,展示数据的分布情况)
x=randn(1000,1);
histogram(x,'Normalization','probability');//对数据进行了概率密度归一化
bar(绘制条形图,对不同数据进行展示)
>> x=categorical({'A','B','C','D','E'});
>> y=[3 5 2 7 4];
>> bar(x,y)
pie(绘制饼函数,展示不同的占比情况)
>> x=[25 35 20 15 10];
>> labels={'A','B','C','D','E'};
>> pie(x,labels);
stem(绘制离散数据的垂直线段图)
>> x=0:0.1:2*pi;
>> y=sin(x);
>> stem(x,y);
pcolor(绘制伪彩色图)
>> [X,Y]=meshgrid(-2:0.1:2);
>> Z=X.^2+Y.^2;
>> pcolor(X,Y,Z);
>> shading interp;
errorbar(绘制带误差线的线图,展示数据的变化范围以及置信区间)
>> x=1:5;
>> y=[3 5 2 7 8];
>> e=[0.5 1 0.3 1.2 0.8];
>> errorbar(x,y,e,'o','MarkerSize',10,'LineWidth',2);
rose(绘制极径图,展示数据的极向分布)
>> x=2*pi*rand(1,1000);
>> rose(x);
boxplot(绘制箱线图,展示分布情况和异常值)
>> x=[randn(100,1);5+0.5*randn(50,1)];
>> g=[zeros(100,1);ones(50,1)];
>> boxplot(x,g,'Labels',{'Group 1','Group 2'});
polarhistogram(绘制极坐标直方图,展示数据的极向分布)
>> x=2*pi*rand(1,1000);
>> polarhistogram(x,20);
wordcloud(绘制词云图,展示文本数据的词频分布)
txt=fileread("文件.txt")
wordcloud(txt);

3.函数与方程
1.常用函数
| 主题词 | 意义 |
|---|---|
| polyval | 多项式求值(作用在多项式系数和x向量求y向量,返回n次多项式p在x的值) |
| conv | 多项式的乘积 |
| deconv | 多项式的除法 |
| roots | 求多项式的根 |
| feval | 函数求值 |
| inline | lnline函数 |
| fzero | 求一元函数实根 |
| fsolve | 方程组数值求解 |
| fminbnd | 一元函数求值 |
| fminserach | 多元函数求值 |
| isqcurvefit | 曲线拟合 |
| polyfit | 多项式拟合 |
2.求根
-
roots
roots函数用于求解多项式方程的根,即找到多项式在复数域中的所有根,它的输入是一个包含多项式系数的向量,输出是一个包含多项式在复数域中所有根的向量,roots函数使用的是拉格朗日-牛顿插值法,通过对多项式进行插值来计算多项式的根,因此,roots函数适用于求解多项式方程的根,但不能用于求解非多项式的根。
%函数表达式
syms x
f=(2.*x+3).^3-4;
%将多项式进行展开
f_v=expand(f)%8*x^3 + 36*x^2 + 54*x + 23
%展开后提取系数
p=[8,36,54,23];
%对多项式进行求根
value=roots(p)
polyval(p,value)-
fzero
fzero函数用于求解单变量非线性方程的零点,即在给定的区间内找到函数的一个根,它使用的是单点迭代法(牛顿迭代法),通过不断逼近函数的零点来计算方程的解,因此,fzero函适用于求解多变量非线性方程组的根
>> %函数表达式
>> f=@(x)(2.*x+3).^3-4;
>> %区间
>> x=[-3,3];
>> %求解方程的零点
>> x=fzero(f,x);
>> %输出结果
>> disp(x)
-0.7063-
fsolve(非线性方程)
%定义非线性方程组
f=@(x)[9*x(1)^2+36*x(2)^2+4*x(3)^2-36;x(1)^2-2*x(2)^2-20*x(3);16*x(1)-x(1)^3-2*x(2)^2-16*x(3)^2];
%初始值
x=[1;1;1];
%求解方程组
x=fsolve(f,x);
%输出结果
disp(x)3.多项式拟合
-
polyfit
polyfit是MATLAB中用于多项式拟合的函数,它可以根据给定的数据点,拟合出一个给定次数的多项式函数(x,y,n)
-
polyval
计算拟合结果
注意:多项式拟合并不一定能够完全恢复原始数
[x,fval]=fminbnd(fun,x1,x2)据的特征,当拟合多项式次数过高时,可能会出现拟合的情况,导致拟合结果对于噪声过于敏感,从而失去了真实数据的预测能力,因此,在进行多项式拟合时,需要根据具体的数据特征和拟合目标,选择合适的多项式次数,避免出现过拟合或欠拟合的情况。
4.函数极值
-
fminbnd(求解单变量有界函数最小值)
注意:‘fun’表示待求解的单变量有界函数,可以是一个函数句柄,一个匿名函数或一个函数字符串;‘x1’和‘x2’分别为待求解区间的左右端点,即函数的取值范围,函数的输出结果包括了一个标量‘x’,表示函数的最小值点,以及一个标量‘fval’,表示函数在最小值点的取值。
该函数使用的是黄金分割法,通过不断的狭窄区间范围来逐步逼近函数的最小值点,因此,该函数适用于求解单变量有界函数的最小值,但不能用于求解多变量函数的最小值,无界函数的最小值或非连续函数的最小值。
5.微积分
| 主题词 | 意义 |
|---|---|
| diff | 导数(数值差分) |
| gradient | 数值导数和梯形 |
| polyder | 多项式求导 |
| quiver | 方向导数图 |
| trapz | 梯形积分法 |
| quadl | 高精度积分 |
| int | 积分 |
| integral | 高精度积分 |
| dblquad | 矩阵二重积分 |
| quad2d | 二重积分 |
| integral2 | 二重积分 |
| triplequad | 矩阵三重积分 |
| integral3 | 三重积分 |
4.符号函数和符号矩阵
概念:函数计算是使用符号表达式来计算数学计算,而不是数值计算,符号表达式包含符号变量和数学运算符,可以表示数学公式、方程、函数等。符号计算可以进行求导、积分、解方程、化简等操作,得到的结果也是符号表达式,具有高精度和通用性。
在matlab中,可以使用符号工具箱进行符号计算,符号工具箱提供了一组函数和工具,用于创建、操作、化简符号表达式,以及进行符号积分、符号求导、符号求解等操作,使用符号工具箱进行符号变量和运算符来构造符号表达式。
符号计算和作用指令
| 主题词 | 意义 |
|---|---|
| sym | 将数值或字符转化为符号 |
| symfun | 定义符号函数 |
| syms | 定义符号变量或函数 |
| subs | 变量替换 |
| digits | 定义数值精度 |
| vpa | 任意精度计算 |
| double | 将符号对象转换为数值 |
| char | 将符号对象转换为字符串 |
| factor | 因式分解 |
| expand | 展开式 |
| collect | 合并同类项 |
| finverse | 求函数逆 |
| compose | 求复合函数 |
| simplify | 化简 |
| simple | 化为最短形式 |
| numden | 分时通分 |
| funtool | 函数计算器 |
| limit | 符号极限 |
| symsum | 级数求和 |
| diff | 求导函数 |
| taylor | 泰勒展开 |
| taylortool | 泰勒展开计算器 |
| jacobian | Jacobi矩阵 |
| int | 积分 |
| solve | 解方程 |
| vpasolve | 方程数值解 |
| dsolve | 解微分方程 |
| ezplot | 简捷函数曲线 |
| ezpolar | 极坐标图 |
| ezplot3 | 空间曲线 |
| ezmesh | 网面 |
| ezsurf | 曲面 |
| ezcontour | 等高线 |
| latex | 公式的Latex公式 |
| ccode | 公式的C代码 |
| matlabFunction | 公式的MATLAB代码 |
| evalin | 调用Mupad计算 |
| mupad | 调用Mupad计算 |
1.符号对象
符号对象是一种特殊的数据类型,称为符号对象,用字符串形式表达,但又不同于字符串,符号运算中的变量、函数和表达式都是符号对象。
>> %数值表达式
>> n=pi*2;
>> %数值转换为符号对象
>> a=sym(n);
>> %定义符号变量以及符号计算表达式
>> syms x y c
>> d=x^3+2*y^2;
>> %定义符号矩阵
>> A=[x,y;2*x,2*y]
A =
[ x, y]
[ 2*x, 2*y]
>> A=subs(A,x,c)
A =
[ c, y]
[ 2*c, 2*y]2.计算精度和数据类型转换
符号数值计算默认精度为32位十进制,是MATLAB数值计算的两倍,符号工具箱号提供了计算精度设置指令,可以定义任意精度的数值计算。

>> %s为圆周率
>> s=pi
s =
3.1416
>> %将数值计算精度设置为8位
>> digits(8)
>> %求s的数值结果
>> x=vpa(s)
x =
3.1415927
>> %采用n位计算精度求s的数值结果
>> x=vpa(s,n)
x =
3.14159
>> x=vpa(s,4)
x =
3.142
>> %符号对象转换为双精度
>> double(s)
ans =
3.1416
>> %符号对象转换为字符串
>> char(s)3.符号矩阵和符号函数
MATLAB大部分矩阵和数组运算符及指令都可以应用于符号矩阵,大部分MATLAB数学函数和逻辑关系运算也可以用于符号对象。
>> %f(x,y)=(x-y)^3
>> %g(x,y)=(x+y)^3
>> %定义符号变量
>> syms x y;
%定义函数
>> f=(x-y)^3;
>> g=(x+y)^3;
%两个函数相乘
>> h=f*g;
%展开多项式
>> hs=expand(h)
hs =
x^6 - 3*x^4*y^2 + 3*x^2*y^4 - y^6
%因式分解
>> hf=factor(hs)
hf =
[ x - y, x - y, x - y, x + y, x + y, x + y]
%定义符号函数,自变量是xy
>> fun=symfun(f*g,[x,y])
fun(x, y) =
(x + y)^3*(x - y)^3
%符号计算替换无需使用subs方法
>> s=fun(x,x^2+x+1)
s =
-(x^2 + 1)^3*(x^2 + 2*x + 1)^3
>> %合并同类项,变量x
>> scol=collect(s,x)
scol =
- x^12 - 6*x^11 - 18*x^10 - 38*x^9 - 63*x^8 - 84*x^7 - 92*x^6 - 84*x^5 - 63*x^4 - 38*x^3 - 18*x^2 - 6*x - 1
>> %化简
>> ssim=simplify(scol)
ssim =
-(x^2 + 1)^3*(x + 1)^6
%数学公式的Latex输出
latex(ssim)
ans =
'-{\left(x^2+1\right)}^3\,{\left(x+1\right)}^6'
%数学公式的C语言代码
ccode(ssim)
ans =
' t0 = -pow(x*x+1.0,3.0)*pow(x+1.0,6.0);'
%数学公式的matlab匿名函数代码
matlabFunction(ssim)
ans =
包含以下值的 function_handle:
@(x)-(x.^2+1.0).^3.*(x+1.0).^64.符号微积分
-
符号函数的极限limit(f,x,a)
f为所求极限的函数,x为变量,a为常数,求函数f关于变量x在a点处的极限,a和x都可以省略,若x省略,则x默认为是系统自变量,若a省略,a的默认值为0,若f的左右极限不等,还可以求单边极限:
limit(f,x,a,'right') limit(f,x,a,'left')
-
符号函数的导数diff(f,x,n)
函数f关于变量x的n阶导数,n是多少就是对目标函数求几阶导数
-
符号函数的积分int(f,x,a,b)
定积分:int(f,x) 不定积分:int(f,x,a,b) inf为无穷大

>> %定义符号变量
>> syms n x;
>> %定义表达式
>> f=(1+x/n)^n;
>> g=(-1)^n*x^n/n;
>> %符号极限的计算,变量n趋向于正无穷大
>> limit(f,n,inf)
ans =
exp(x)
>> %离散求和,变量n从1到无穷
>> symsum(g,n,1,inf)
ans =
piecewise(x == -1, Inf, abs(x) <= 1 & x ~= -1, -log(x + 1))2.Matlab常规应用
1.分段函数

-
使用匿名函数
>> %定义分度函数
>> f=@(x)(x>1).*x.^2+(-1<=x&x<1).*1+(x<=-1).*(3+2*x);
>> %生成x向量
>> x=linspace(-2,2,1000);
>> %计算y向量
>> y=f(x);
>> %绘制函数曲线
>> plot(x,y)
//设置网格曲线
>> grid on
%x坐标名称
>> xlabel('x')
#y坐标名称
>> ylabel('y')
%题目
>>title('分段函数f(x)')
legend('表达式1','表达式2') 
-
使用分段函数
编辑一个part脚本函数
function y=part(x)
n=length(x);
for i=1:n
if x(i)>1
y(i)=x(i).^2;
elseif x(i)>-1
y(i)=1;
else
y(i)=3+2*x(i);
end
end
end-
通过find获取下标
>> x=linspace(-2,2,1000);
>> y=zeros(size(x));
>> ind1=find(x>1);%第一段函数的下标
>> ind2=find(x>-1&x<=1);%第二段函数的下标
>> ind3=find(x<=-1);%第三段函数的下标
>> y(ind1)=x(ind1).^2;%第一段函数
>> y(ind2)=1;%第二段函数
>> y(ind3)=3+2*x(ind3);%第三段函数2.三维平面图
-
mesh绘图
>> %meshgrid函数用于生成二维网格矩阵,从而方便地生成网格图或三维图形
>> [X,Y]=meshgrid(-2:0.1:2);%相当于生成区间
>> %三维表达式
>> Z=X.^2-Y.^2;
>> %mesh方法绘制三维网格图
>> mesh(X,Y,Z);
>> xlabel('x');
>> ylabel('y');
>> zlabel('z');
>> title('三维网格图'); 
-
surf绘图
>> %生成数据
>> %meshgrid函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形
>> [X,Y]=meshgrid(-2:0.1:2);%相当于生成区间
>> %三维表达式
>> Z=X.^2-Y.^2;
>> %surf方法绘制三维曲面图
>> surf(X,Y,Z);
>> xlabel('x');
>> ylabel('y');
>> zlabel('z');
>> title('三维曲面图'); 
-
使用contour方法绘制等高线
>> %生成数据
>> %meshgrid函数可以用于生成二维网格矩阵,从而方便地生成网格图或三维图形
>> [X,Y]=meshgrid(-2:0.1:2);%相当于生成区间
>> %三维表达式
>> Z=X.^2-Y.^2;
>> %contour方法绘制三维网格图
>> contour(X,Y,Z);
%如果想要确定某一等高线直接在后面添加参数
%contour(X,Y,Z,[1]);
>> xlabel('x');
>> ylabel('y');
>> zlabel('z');
>> title('三维等高线'); 
3.三维线性图
-
使用plot3绘制三维线条
>> %生成数据
>> t=linspace(0,10*pi,1000);
>> x=sin(t);
>> y=cos(t);
>> z=t;
>> %绘制三维线条图
>> plot3(x,y,z);
>> xlabel('x');
>> ylabel('y');
>> zlabel('z');
>> title('三维线条图'); 
4.矩阵运算(线性方程组求解问题)
使用rref化为行最简化求方程组的解答

>> %根据线性方程组得到矩阵A,b
>> A=[1 -1 1 -1;-1 1 1 -1;2 -2 -1 1];
>> b=[1;1;-1];
>> %只有当矩阵A的秩和增广矩阵(A,b)秩相等才有解答
>> if rank(A)==rank([A,b])
%使用rref求增广矩阵行最简
rref([A,b])
else
disp('次方程组无解')
end
ans =
1 -1 0 0 0
0 0 1 -1 1
0 0 0 0 0正交变换--将二次型化为标准型
首先根据给出的公式写出矩阵A,通过矩阵A求特征值和特征向量,正交化,规范化然后求出标准化
normalize.m(规范化)文章来源:https://www.toymoban.com/news/detail-718339.html
function V_norm=normalize(V)%定义规范函数
%对向量进行规范化
[m,n]=size(V);
for i=i:n
V_norm(:,i)=V(:,i)/norm(V(:,i));
end
endgramSchmidt.m(正交化)文章来源地址https://www.toymoban.com/news/detail-718339.html
function [Q,R]=gridSchmidt(A)
%Gram-Schmidt 正交化过程
[m,n]=size(A);
Q=A;
R=zeros(n,n);
for j=1:n
R(j,j)=norm(Q(:,j));
Q(:,j)=Q(:,j)/R(j,j);
for i=j+1:n
R(j,i)=Q(:,j)*Q(:,i);
Q(:,i)=Q(:,i)-R(j,i)*Q(:,j);
end
end
end到了这里,关于Matlab基础知识汇总(小白速成)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!













