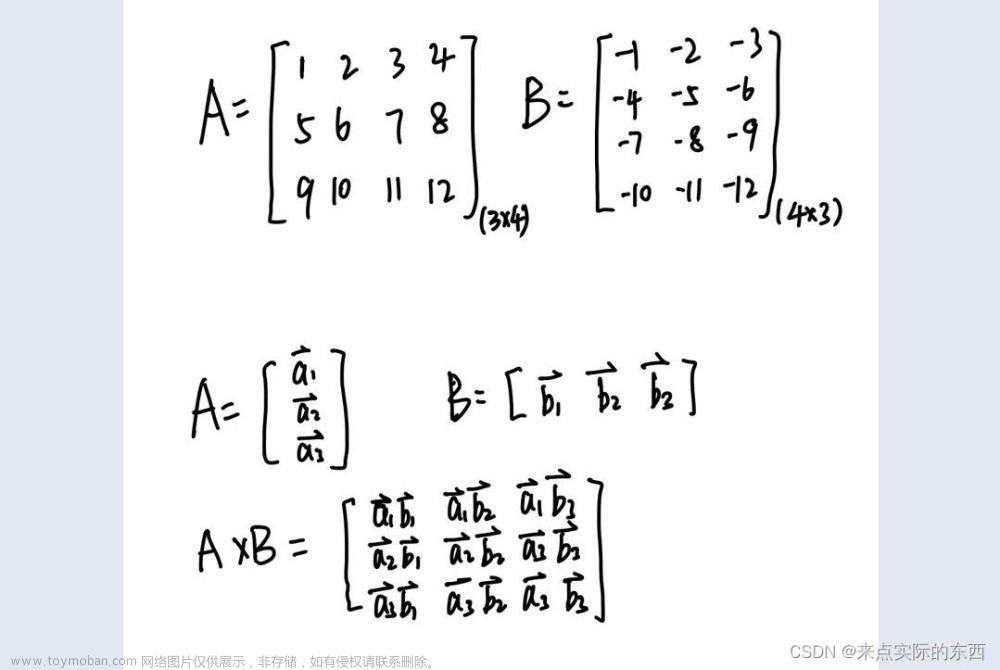
首先理了解矩阵是什么:
矩阵是一个按照长方阵列排列的复数或实数集合。(相信大家都懂)
关于矩阵的基本概念:
1.方阵:n 阶方阵 (正方形嘛)
2.同型矩阵:两个矩阵,行数与列数对应相同,称为同型矩阵
ok进入主题:
矩阵加减法:
在了解矩阵乘法前先看看矩阵加减法:
1.两个矩阵进行一般的加法运算的前提是两个矩阵为同型矩阵2.具体操作如图
2.具体操作如图(减法同理)

3.在矩阵的加法运算中,满足交换律和结合律,也就是
A+B=B+A;A+(B+C)=(A+B)+C;
到这里相信都很简单
矩阵乘法(上点难度嘿嘿嘿)
1.矩阵的乘法是向量内积的推广。
2.矩阵相乘只有在第一个矩阵的列数和第二个矩阵的行数相同时才有意义。
举个栗子:A为n*m的矩阵,B为m*p的矩阵,则C=A*B为n*p的矩阵,并且:
注意:矩阵乘法满足结合律,不满足一般的交换律。
so:利用结合律,矩阵乘法可以利用 快速幂 的思想来优化。
在普通的乘法中,一个数乘1还是等于它本身,在矩阵乘法中也有这么一个“1”,它就是单位矩阵
不同于普通乘法中的单位1,对于不同矩阵他们的单位矩阵大小是不同的
也就是说单位矩阵都是正方形的,这是因为只有正方形的矩阵能保证结果和前一个矩阵形状相同
单位矩阵的元素非0即1,从左上角到右下角的对角线上元素皆为1,其他皆为0
了解了这么多,我们开始看题,矩阵快速幂,由于矩阵乘法满足结合律,所以我们只需要把它按照一般的快速幂打,再重载一下运算符就可以了,好了我们直接放代码
mat operator*(const mat& T) const {
mat res;
for(int i=0;i<sz;i++)
for(int j=0;j<sz;j++)
for(int k=0;k<sz;k++){
res.a[i][j]+=mul(a[i][k],T.a[k][j]);
res.a[i][j]%=mod;
}
return res;
}例题:【模板】矩阵快速幂 - 洛谷
例题讲解:
正如题目所诉这是个模板题有不懂的直接看代码注释:
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int mod=1e9+7;
struct point{
ll c[150][150];//注意long long
}A,ans;
ll n,k;
point operator *(const point &x,const point &y){//重装运算符
point z;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
z.c[i][j]=0;
}
}
//矩阵乘法模板
for(int i=1;i<=n;i++){//枚举行
for(int j=1;j<=n;j++){//枚举列
for(int k=1;k<=n;k++){//枚举两给需要相加的矩阵的列与行(因为两者一样)
z.c[i][j]+=x.c[i][k]*y.c[k][j]%mod;
z.c[i][j]%=mod;
}
}
}
return z;
}
int main(){
cin>>n>>k;//输入
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>A.c[i][j];
}
}
for(int i=1;i<=n;i++){//初始化答案矩阵
ans.c[i][i]=1;//对角线为1
}
while(k>0){//快速幂
if(k&1) ans=ans*A;//注意不能写为ans*=A
A=A*A;
k=k>>1;//相当于k/=2
}
for(int i=1;i<=n;i++){//输出答案
for(int j=1;j<=n;j++){
cout<<ans.c[i][j]<<" ";
}
cout<<"\n";
}
return 0;//完美撒花
}关于快速幂(不懂的可以看看):
1.由于电脑计算需要乘b次这样太慢了。。。(怎么办呢?当然是不要乘b次,这不是废话)
2.so:如果将 a 自乘一次,就会变成 。再把 自乘一次就会变成 。然后是…… 自乘 n 次的结果是。对吧……
3.看看快速幂递推式,这样复杂度从O(k)降为了O(k)

4.递归版代码(有来理解,不然平时题目题解会TLE,如果你不想的话)文章来源:https://www.toymoban.com/news/detail-718753.html
point Fastpower(poitn a,long long b){//求a的b次方
if(b==1) return a;
if(b%2==0) return Fastpower(a,b/2)*Fastpower(a,b/2);
if(b%2==1) return Fastpower(a,b/2)*Fastpower(a,(b-1)/2)*a;
}5.while版:文章来源地址https://www.toymoban.com/news/detail-718753.html
void Fastpower(int b){//求a的b次方
int ans=1;
while(b>0){
if(b&1) ans=ans*a;//相当于b%2==1
a=a*a;
b=b>>1;//相当于b/=2
}
}感谢看到这里希望对你有所帮助,若文章有什么不对的地方一定要提出留个赞在走吧!
到了这里,关于矩阵乘法(矩阵乘矩阵)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!