关于链表的建立与操作
目录
1. 链表的定义
2.单链表的基本操作
3. 循环链表及其操作
4.双向链表及其操作
5.用数组模拟链表
一、链表的定义
因为线性表是静态线性的存储结构,所以为了方便动态地对数据进行处理,我们引入链表这一数据结构。
因为链表是动态的存储结构,所以存储在其中的数据地址不一定是连续的。因此在创建链表时不仅需要保存数据本身,还需保存它的地址。所以我们就用一个结构体来存储链表的结点。其中每个结点都要包含两个领域,分别是数据域和指针域,用于存储数据和存储下一个结点的地址。

typedef struct node{
int data;//这里的data可以是任意数据类型
struct node *link;
}LNode,*LinkList;//命名时LNode *p和LinkList p等效
头结点(指针域存放头指针)
二、单链表的基本操作
1.创建一个单链表
单链表需要一个头指针list来指出第一个结点的位置。并且在创建结点的时候也需要用一个活动的指针来往后遍历。初始时(没有结点),让头指针list指向NULL。在创建结点的时候,需要先用new动态内存分配函数来给结点申请存储空间(如果用malloc函数的话需要加头文件,c语言中头文件为#include<alloc.h>,在c++中则是#include <cstdlib>),再往头指针后面依次插入n个结点(插入操作在下文会详细论述)。
LinkList CREATE(int n)
{
LinkList list=NULL;
LinkList p;//活动指针
Linklist r;//放置于最后一个结点之前
int a;
for(int i=0;i<n;i++)
{
p=new LNode;
p->data=a;
p->link=list;
if(list==NULL)
list=p;
else
r->link=p;
r=p;
}
return list;
}
2.求线性链表的长度
要求链表的长度,直观的反映为结点的数量,我们只需要设置一个活动的指针,让它从头遍历到尾,每遍历一个结点就让记录结点的数加1,直到遍历到末尾。
int LENGTH(LinkList &list)
{
LinkList p=list;//在初始的时候让p等于头指针,指向第一个结点
int n=0;//n就是链表的长度(反映结点数)
while(p->link!=NULL)
{
p=p->link;//p往后遍历
n++;//p每遍历一次就让结点数+1
}
return n;
}
3.测试链表是否为空
如果链表为空的话,头指针指向的就是NULL了,判断一下就好,为空返回真,非空返回假
bool EMPTY(LinkList list)
{
return list==NULL;
}
4.确定item在链表中的位置
这个操作和第1个操作其实是相似的,第1个操作就是把这个操作的item设定为最后一个结点。所以这个操作的思路也是用一个活动的指针p来遍历,知道某个结点的数据域与item相等。最终返回item的地址
LinkList FIND(LinkList list,int item)
{
LinkList p=item;
while(p->data!=item)
p=p->link;
return p;
}
5.在头结点后面插入结点
头指针list指向的是头结点,所以要在头结点后插入结点就需要通过更改头指针来进行操作。因为插入的结点都是将是第一个结点,所以最终list指向的就应该是插入的结点

void INSERTLINK1(LinkList &list,int item)
{
LinkList p;
p=new LNode;//申请空间
p->data=item;//存入数据
p->link=list;//让p指向头指针指向的结点
list=p;//让头指针指向p
}
6.在链表末尾插入结点
在末尾插入结点,需要最后一个结点的前驱结点r。因为指针域存放的是下一个结点的地址,所以如果要插入结点就需要知道它的前驱结点位置r。实现这步操作用r遍历到倒数第二个结点即可。操作的结果是插入的结点是最后一个结点,则它的指针域存放的就是NULL了

void INSERTLINK2(LinkList list,int item)
{
LinkList r=list;
LinkList p;
while(r->link!=NULL)//如果是最后一个的话条件就是r!=NULL
{
r=r->link;
}
p=new LNode;
p->data=item;
p=NULL;
r->link=p;
}
7.在q结点后面插入结点
要在q结点后面插入结点,在函数的参数里就需要加入q的地址。当然,如果q结点也可能是头结点(结点的指针域里存放的是头指针的结点就是头结点),所以需要判断一下。
void INSERTLINK3(LinkList &list,LinkList &q,int item)
{
LinkList p;
if(list==NULL)//链表为空时,就是在头结点后面插入结点
{
INSERTLINK1(list,item);
}
else
{
p->data=item;
p->link=q->link;
q->link=p;
}
}
8.在第n个结点后面插入结点
与7不同,我们只知道第i个结点的编号,但是并不知道它的地址。所以我们就需要通过遍历到第n个结点来求得它的地址。有可能出现链表里不存在第n个结点的情况,所以需要判断一下。
void INSERTLINK4(LinkList &list,int item,int n)
{
LinkList r=list;
LinkList p;
int j=1;
while(j<n&&q!=NULL)//j<n遍历得到的是第n-1个结点,也就是前驱结点
{
r=r->link;
j++;
}
if(j!=n||j==NULL)
{
cout<<"不存在第i个结点";
}
else
{
p=new LNode;
p->data=item;
p->link=r->link;
r->link=p;
cout<<"插入成功";
}
}
9.在按值有序链接的链表中插入一个item的结点
如果链表要保持按值有序,就需要根据item的值找到插入的位置。注意判断链表是否为空
void INSERTLINK5(LinkList &list,int item)
{
LinkList p;
p=new LNode;
p->data=item;
if(list==NULL||item<(list->data))//链表为空和插入值最小的情况都是插在头结点之前
{
p->link=list;
list=p;
}
else//寻找插入位置
{
LinkList q=list,r;//插入的位置就在r,q之间
while(item>=(q->data)&&q->link!=NULL)
{
r=q;
q=q->link;
}
p->link=q;
r->link=p;
}
}
10.从非空链表中删除q结点
在删除操作中,我们需要知道结点的前驱结点r和后继结点(q->link)的地址,方便修改指针。但是知道了前驱结点就可以通过指针知道后继结点。
在删除结点后,需要用free()来将删除结点的空间释放掉

void DELETELINK1(LinkList &list,LinkList &q)
{
LinkList r=list;
if(q==list)//当q为头结点时
{
list=q->link;
free(q);
}
else
{
while(r->link!=q&&r->link!=NULL)
r=r->link;
if(r->link!=NULL)
r->link=q->link;
free(q);
}
}
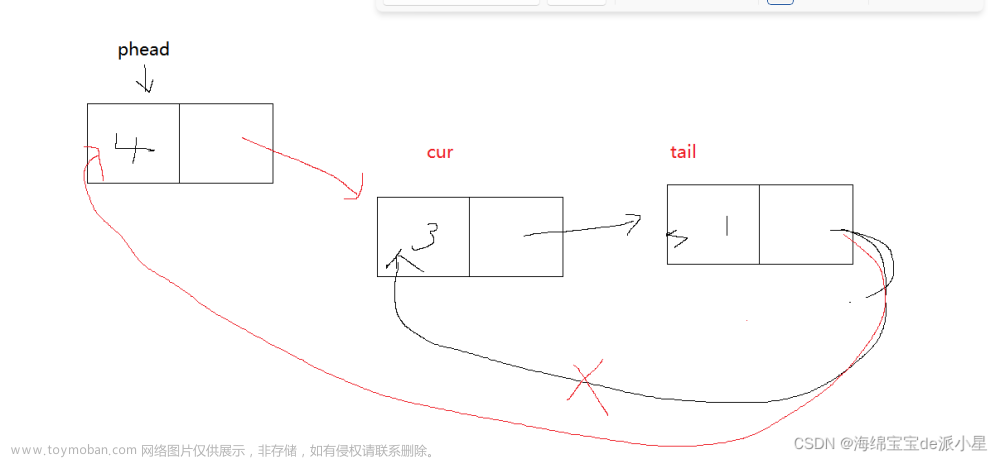
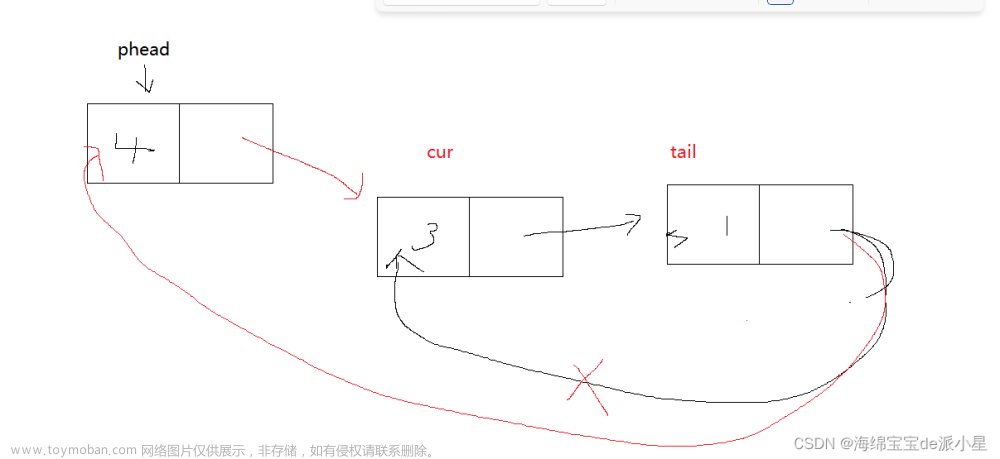
11.逆转一个链表(较难理解)
在逆转链表时,需要3个变量p,q,r,其中让p在头部,让q在尾部,从第二个结点开始,让第二个结点的指针指向头结点(逆转),每一次循环都只逆转一个结点的指针。
p是从list一直往后遍历的指针;q从NULL先变成list,再逐步往后遍历,顺序在p之前;r先为空,后执行和q一样的操作,位置在q之前。
void INVERT(LinkList &list)
{
LinkList p,q,r;
p=list;
q=NULL;
while(p!=NULL)
{
r=q;
q=p;
p=p->link;
q->link=r;
}
list=q;
}
12.将两个非空链表连接成一个链表
设两个链表的头指针为lista和listb,将第二个头指针连接到第一个链表末尾即可(末尾位置用遍历寻找)
void CONNECT(LinkList lista,LinkList listb)
{
LinkList p;
for(p=lista;p!=NULL;p=p->link);//执行完p就到a链表的末尾了
p->link=listb;
}
13.将按值有序的两个链表合并
设两个链表头指针为lista和listb,合并后为listc。
需设置3个指针p,q,r。p,q分别指向a和b待比较的结点,r指向c中最后的结点(r->link=NULL)。
不断比较p->data和q->data,符合条件的就连接到r后面
当其中一个链表为空时,将另一个中剩余的结点连接到r所指结点后。
初始时,listc指向lista和listb中较小的那个。
LinkList MERGELIST(LinkList lista,LinkList listb)
{
LinkList p=lista,q=listb,r,listc;
if((lista->data)<=(listb->data))//先判断头结点的大小
{
listc=lista;
r=lista;
p=lista->link;
}
else
{
listc=listb;
r=listb;
q=listb->link;
}
while(p!=NULL&&q!=NULL)//对后面的结点进行比较
{
if((p->data)<=(q->data))
{
r->link=p;
r=p;
p=p->link;
}
else
{
r->link=q;
r=q;
q=q->link;
}
}
r->link=p?p:q;
return listc;
}
14.复制一个链表(递归)
假设已知链表用lista指出,复制后产生的链表由listb指出。
算法思路:
若lista为空,返回空指针;
若lista非空,复制lista所指结点,将其指针赋予listb,再复制其后继结点,将其指针赋予 listb->link,最后返回新复制的头指针listb
LinkList COPY(LinkList lista)
{
LinkList listb;
if(lista==NULL)
return NULL;
else
{
listb=new LNode;
listb->data=lista->data;
listb->link=COPY(lista->link);
}
return listb;
}
三、循环链表及其操作
在线性链表中,如果知道了某个链结点的指针,我们可以很方便的访问后续的结点,但是没有办法访问这之前的结点。所以,引入循环链表和双向链表,这两种链表可以在知道任意一个结点地址的情况下访问其他任意一个结点。这里先对循环链表进行讨论。
循环链表的尾指针不放NULL,而是指向链表的头指针。
循环链表的操作和前面的基本相同,但是循环条件并不是判断指针是否等于NULL,而是是否等于头指针。在设计链表时,可以省去尾指针。
例:在一个带有头结点的循环链表中查找一个数据为item的结点,存在返回该结点指针,否则返回NULL
LinkList SEARCHKEY(LinkList list,int item)
{
LinkList p;
p=list->link;
while(p!=list)
{
if(p->data==item)
return p;
p=p->link;
}
return NULL;
}
四、双向链表及其操作
双向链表和环形链表一样,也可以实现查找任意一个结点的功能。在双向链表中,结点与结点之间可以双向移动,每个结点有三个数据域,数据域、左指针域和右指针域
因此对于双向链表的结构体可以定义为:
tyepdef struct node
{
int data;
struct node *llink,*rlink;
}DNode,*DLinkList;
双向链表的结构可以这样表示:
同时也可将双向链表和循环链表结合。
接下来是双向链表的插入与删除操作
1.在带有头结点的双向循环链表中第一个数据域内容为x的结点右边插入一个数据信息为item的结点
这里的数据域内容为x的结点是从左往右第一个内容为x的结点,而不是所有内容为x的结点。因此先从链表中找到满足条件的链结点,用活动指针q指出,再申请一个p结点,作为插入的新结点。将q的地址送到p结点的左指针域(llink),再将q的后继结点地址(q->rlink)送到p结点的右指针域中(rlink),然后将新结点的地址p送到q的后继结点的左指针域中(rlink),最后将p的地址送到q的右指针域中。
算法如下:
int INSERTD(DLinkList list,int x,int item)
{
DLinkList p,q;
q=list->rlink;
while(q!-list&&q->data!=x)
q=q->link;
if(q==list)
return -1;
p=new LNode;
p->data=item;
p->llink=q;
p->rlink=q->rlink;
q->rlink->llink=p;
q->rlink=p;
return 1;
}
2.从带有头结点的双向循环链表中删除第1个数据域为x的结点
先从链表中找到符合条件的结点,用活动指针q指出。将q所指结点的后继结点的地址送入q所指结点的前驱结点的右指针域,同时将q的前驱结点的地址送入后继结点的左指针域中,然后释放q的存储空间。(整个过程只需更改2个指针)
int DELETED(DLinkList list,int x)
{
DLinkList q;
q=list->link;
while(q!=list&&q!=x)
q=q->link;
if(q==list)
return -1;
q->llink->rlink=q->rlink;
q->rlink->llink=q->llink;
free(q);
return 1;
}
五、用数组模拟链表
有一些编程语言没有结构体,为了实现这种数据结构可以用数组进行模拟,用数组的下标来表示结点的地址。
1.单链表
在一个单链表中有很多结点,其中有很多数据域和指针域。我们用两个数组来分别表示数据域和指针域(value[N]和ne[N])
用一个整形变量来表示当前已经用到了哪个点(idx)
const int N=1e5+10;//数组的大小(结点的数量)
int value[N],ne[N],idx,head;
int x;//x代表输入的data
int k;//k代表输入的位置
void init()//初始化
{
head=-1;//初始时链表里没有结点,头指针为空
idx=0;//当前用过的结点数为0
}
void add_to_head(int x)//在链表头部插入结点
{
value[idx]=x;
ne[idx]=head;
head=idx++;
}
void deletes(int k)//删除k结点
{
ne[k]=ne[ne[k]];
}
void add(int k,int x)//在k结点的左边插入x
{
value[idx]=x;
ne[idx]=ne[k];
ne[k]=idx++;
}
2.双链表
双链表的思路与上文一样,比单链表多一个指针域,所以我们再多开一个数组保存另一个指针域。文章来源:https://www.toymoban.com/news/detail-718896.html
const int N=1e5+10;
int idx=2;
int m;
int x;
int k;
int value[N],l[N],r[N];
void init()
{
l[0]=1;
l[1]=0;
}
void add_to_right(int k, int x) //在k点右边插入一个数
{
value[idx]=x;
r[idx] = r[k];
l[idx] = k;
l[r[k]] = idx;
r[k] = idx++;
}
void add_to_left(int k, int x) //或者调用上个函数add_to_right(l[k],x)
{
value[idx] = x;
r[l[k]] = idx;
r[idx] = k;
l[idx] = l[k];
l[k] = idx++;
}
void deletes(int k)
{
l[r[k]] = l[k];
r[l[k]] = r[k];
}
链表作为一个动态的存储结构在数据的增删改查方面比静态的线性表要方便很多,它不要求结点逻辑上的位置相邻,仅通过指针来映射数据元素之间的逻辑关系。链式存储结构不仅可以用来存储线性表,还可以用来存储各种非线性的数据结构,如树和图等。文章来源地址https://www.toymoban.com/news/detail-718896.html
到了这里,关于关于链表的建立与操作(c++实现)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!