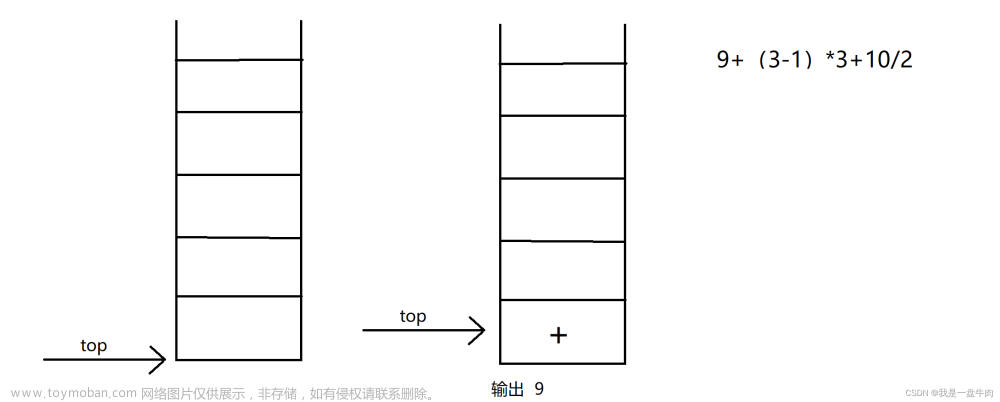
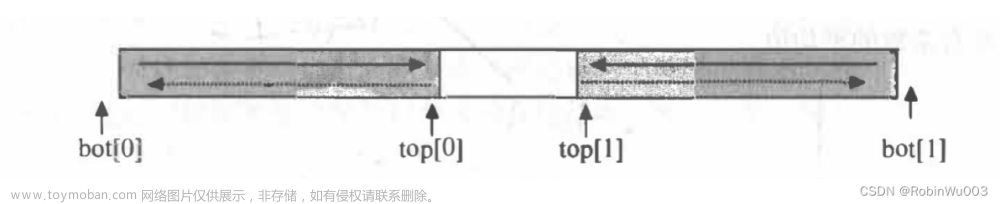
什么是前缀表达式、中缀表达式、后缀表达式
前缀表达式、中缀表达式、后缀表达式,是通过树来存储和计算表达式的三种不同方式
以如下公式为例
( a + ( b − c ) ) ∗ d ( a+(b-c) )*d (a+(b−c))∗d
通过树来存储该公式,可以表示为

那么问题就来了,树只是一种抽象的数据结构,它必须要通过某个形式的文本来才能存储和输入
此时,就有了三种表示方法:前缀表达式、中缀表达式、后缀表达式
它们分别相当于树的前序遍历、中序遍历、后序遍历,前中后指的是遍历时符号的遍历顺序
前序遍历:符号 - 左操作数 - 右操作数
中序遍历:左操作数 - 符号 - 右操作数
后序遍历:左操作数 - 右操作数 - 符号
中缀表达式
上面的公式,中序遍历的结果为
a + b − c ∗ d a+b-c*d a+b−c∗d
显然,这种表达方式是有歧义的,比如ab是一颗子树,cd是一颗子树,最后相减,遍历结果和上面是一样的
所以中缀表达式必须借助括号,才能正确地表达出想要的结果
中缀表达式的表示结果为
( a + ( b − c ) ) ∗ d (a+(b-c))*d (a+(b−c))∗d
这种表达方式,符合人类的阅读习惯
前缀表达式
上面的公式,先序遍历的结果为
∗ + a − b c d *+a-bcd ∗+a−bcd
这种表达方式是没有歧义的,可以直接作为前缀表达式的结果
这种表达方式,符合计算机的处理习惯,程序可以很容易地解析这种表达式
具体如何解析,下面会给出代码
后缀表达式
上面的公式,后序遍历的结果为
a b c − + d ∗ abc-+d* abc−+d∗
这种表达方式,也符合计算机的处理习惯,解析也很简单
相对于前缀表达式来说,后缀表达式的符号读取顺序,和人类阅读习惯是一致的
因此实际计算机程序中,基本都是用后缀表达式来存储公式的,前缀表达式效果次之
对于中缀表达式,我们则可以先将其转为后缀表达式,再进行求值
通过树结构存储和求值表达式
实现思路比较简单,如果节点上存的是参数,那么该参数的值,就是该节点的值
如果节点上存的操作符,拿该节点左子树和右子树做对应运算,得到的结果作为该节点的值
import java.util.LinkedHashMap;
import java.util.Map;
public class Demo {
//( a+(b-c) )*d
public static TreeNode createTree() {
TreeNode a = new TreeNode();
a.data = "a";
TreeNode b = new TreeNode();
b.data = "b";
TreeNode c = new TreeNode();
c.data = "c";
TreeNode d = new TreeNode();
d.data = "d";
TreeNode e = new TreeNode();
e.data = "e";
TreeNode f = new TreeNode();
f.data = "f";
TreeNode g = new TreeNode();
g.data = "g";
TreeNode op1 = new TreeNode();
op1.data = "*";
TreeNode op2 = new TreeNode();
op2.data = "+";
op1.add(op2);
op1.add(d);
TreeNode op3 = new TreeNode();
op3.data = "-";
op2.add(a);
op2.add(op3);
op3.add(b);
op3.add(c);
return op1;
}
//( 3+(4-2) )*10
public static Map<String, Integer> createParam() {
Map<String, Integer> map = new LinkedHashMap();
map.put("a", 3);
map.put("b", 4);
map.put("c", 2);
map.put("d", 10);
return map;
}
public static int getNodeValue(TreeNode<String> node, Map<String, Integer> param) {
String data = node.data;
switch (data) {
case "+": {
TreeNode<String> leftValue = node.children.get(0);
TreeNode<String> rightValue = node.children.get(1);
return getNodeValue(leftValue, param) + getNodeValue(rightValue, param);
}
case "-": {
TreeNode<String> leftValue = node.children.get(0);
TreeNode<String> rightValue = node.children.get(1);
return getNodeValue(leftValue, param) - getNodeValue(rightValue, param);
}
case "*": {
TreeNode<String> leftValue = node.children.get(0);
TreeNode<String> rightValue = node.children.get(1);
return getNodeValue(leftValue, param) * getNodeValue(rightValue, param);
}
case "/": {
TreeNode<String> leftValue = node.children.get(0);
TreeNode<String> rightValue = node.children.get(1);
return getNodeValue(leftValue, param) / getNodeValue(rightValue, param);
}
default:
return param.get(data);
}
}
public static int compute(TreeNode<String> expression, Map<String, Integer> param) {
return getNodeValue(expression, param);
}
public static void main(String[] args) {
TreeNode tree = createTree();
Map<String, Integer> param = createParam();
int result = compute(tree, param);
System.out.println(result);
}
}
前缀表达式解析和求值
∗ + a − b c d *+a-bcd ∗+a−bcd
首先,我们来观察下前缀表达式的规律
可以发现,每当连续出现两个数值时,前面必定会有一个操作符,这是先序遍历的特征决定的
我们将三个元素取出来进行运行,就可以得到一个操作符节点的数值
如此反复递归,最终就能求出表达式的值
import java.util.*;
@SuppressWarnings("all")
public class Demo {
//表达式
final List expression = new ArrayList();
//变量值
final Map<String, Integer> param = new LinkedHashMap();
//用于读取表达式的栈
final LinkedList stack = new LinkedList();
//( a+(b-c) )*d
//( 3+(4-2) )*10
public void createExpression() {
expression.clear();
expression.add("*");
expression.add("+");
expression.add("a");
expression.add("-");
expression.add("b");
expression.add("c");
expression.add("d");
}
//( a+(b-c) )*d
//( 3+(4-2) )*10
public void createParam() {
param.clear();
param.put("a", 3);
param.put("b", 4);
param.put("c", 2);
param.put("d", 10);
}
//计算表达式的值
public int compute() {
stack.clear();
for (Object element : expression)
push(element);
Object top = stack.pop();
return value(top);
}
//( a+(b-c) )*d
//( 3+(4-2) )*10
//元素入栈
//有可以求值的表达式,入栈前先运算,转化为常量再入栈
public void push(Object element) {
//如果栈为空,直接入栈
if (stack.isEmpty()) {
stack.push(element);
return;
}
//如果是操作符,直接入栈
if (isOperator(element)) {
stack.push(element);
return;
}
Object left = stack.getFirst();
//如果是数值,且栈顶元素也是数值,直接取出进行运算,得到数值后再入栈
if (!isOperator(left)) {
stack.removeFirst();
Object right = element;
Object operator = stack.pop();
Integer value = operate(left, right, operator);
push(value);
return;
}
//如果栈顶不是数值,直接入栈
stack.push(element);
}
//计算最小表达式运算结果
public int operate(Object left, Object right, Object operator) {
int L = value(left);
int R = value(right);
switch (operator.toString()) {
case "+":
return L + R;
case "-":
return L - R;
case "*":
return L * R;
case "/":
return L / R;
default:
throw new RuntimeException("unknown operator");
}
}
//获取元素值,元素可能是变量,也可能是常量
public Integer value(Object element) {
if (element instanceof Integer)
return (int) element;
return param.get(element);
}
//判断元素是操作符还是变量或常量
public boolean isOperator(Object element) {
if (element.equals("+"))
return true;
if (element.equals("-"))
return true;
if (element.equals("*"))
return true;
if (element.equals("/"))
return true;
return false;
}
public static void main(String[] args) {
Demo demo = new Demo();
demo.createExpression();
demo.createParam();
int result = demo.compute();
System.out.println(result);
}
}
后缀表达式解析和求值
a b c − + d ∗ abc-+d* abc−+d∗
先来观察下后缀表达式的特点,可以发现
由于后缀表达式相当于树的后序遍历,先遍历左子树,再遍历右子树,最后遍历运算符
所以只要有运算符出现的地方,前面两个元素一定是操作数,这样就可以求出对应子树的值
实现代码和前缀表达式非常像,稍微简单一点点
import java.util.*;
@SuppressWarnings("all")
public class Demo {
//表达式
final List expression = new ArrayList();
//变量值
final Map<String, Integer> param = new LinkedHashMap();
//用于读取表达式的栈
final LinkedList stack = new LinkedList();
//( a+(b-c) )*d
public void createExpression() {
expression.clear();
expression.add("a");
expression.add("b");
expression.add("c");
expression.add("-");
expression.add("+");
expression.add("d");
expression.add("*");
}
//( 3+(4-2) )*10
public void createParam() {
param.clear();
param.put("a", 3);
param.put("b", 4);
param.put("c", 2);
param.put("d", 10);
}
//计算表达式的值
public int compute() {
stack.clear();
for (Object element : expression)
push(element);
Object top = stack.pop();
return value(top);
}
//元素入栈
//有可以求值的表达式,入栈前先运算,转化为常量再入栈
public void push(Object element) {
//如果不是操作符,直接入栈
if (!isOperator(element)) {
stack.push(element);
return;
}
//如果是操作符,取出前两个数值,计算出结果,将结果入栈
Object right = stack.pop();
Object left = stack.pop();
Integer value = operate(left, right, element);
push(value);
}
//计算最小表达式运算结果
public int operate(Object left, Object right, Object operator) {
int L = value(left);
int R = value(right);
switch (operator.toString()) {
case "+":
return L + R;
case "-":
return L - R;
case "*":
return L * R;
case "/":
return L / R;
default:
throw new RuntimeException("unknown operator");
}
}
//获取元素值,元素可能是变量,也可能是常量
public Integer value(Object element) {
if (element instanceof Integer)
return (int) element;
return param.get(element);
}
//判断元素是操作符还是变量或常量
public boolean isOperator(Object element) {
if (element.equals("+"))
return true;
if (element.equals("-"))
return true;
if (element.equals("*"))
return true;
if (element.equals("/"))
return true;
return false;
}
public static void main(String[] args) {
Demo demo = new Demo();
demo.createExpression();
demo.createParam();
int result = demo.compute();
System.out.println(result);
}
}
中缀表达式转后缀表达式
中缀表达式直接求值比较麻烦,所以我们将其转换为后缀表达式,再求值就方便了
中缀表达式转后缀表达式的难点在于,要考虑括号和运算符优先级,这里直接给出方案
看的过程中,大家可以拿个Excel,按照下面的流程和公式,一步步把操作记录下来,这样就很直观,容易理解

注意,如果想理解透彻,一定要亲自推演一遍
因为这个转换算法不是凭空产生的,而是根据后缀表达式的特点反推出来的
只有在亲自推演的过程中,才能深刻地理解为什么要这么做
回到正题,继续说转换方案文章来源:https://www.toymoban.com/news/detail-719073.html
- 创建两个栈,S1用来存输出元素,S2用来存运算符。由于表达式中的运算符是有优先级的,所以必须通过栈来暂存起来
- 从中缀表达式栈顶开始,向栈尾逐个读取元素
- 如果读到操作数,直接加到S1栈尾。因为后缀表达式操作数永远是在运算符前面的
- 如果读到左括号,则直接压入S2栈顶。因为左括号要等到右括号时才能处理
- 如果读到运算符,且S2栈为空或S2栈顶元素为左括号,则直接压入S2栈顶。因为这种情况不需要比较运算符优先级
- 如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级大于栈顶元素,则将当前运算符压入S2栈顶。因为后面读取到的运算符可能比当前运算符优先级更高,因此暂时不能输出当前运算符
- 如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级小于等于栈顶元素,则将S2栈顶运算符弹出,加到S1栈尾。因为优先级高的运算符要先参加运算。注意,这是一个递归过程,因为S2中可能已存在多个运算符,它们的优先级可能都大于等于当前运算符,当这些运算符都弹出时,再将当前运算符压入S2栈顶
- 如果读到右括号,则将S2内首个左括号以上的运算符,全部加到S1栈尾。因为括号的优先级是最高的,立刻进行运算
实现代码如下文章来源地址https://www.toymoban.com/news/detail-719073.html
import java.util.*;
@SuppressWarnings("all")
public class Demo {
//中缀表达式
final List expression = new ArrayList();
//变量值
final Map<String, Integer> param = new LinkedHashMap();
//用于输出结果的双向链表
final LinkedList s1 = new LinkedList();
//用于暂存运算符的栈
final LinkedList s2 = new LinkedList();
// ((a+b*c+d)+e)*f
public void createExpression() {
expression.clear();
expression.add("(");
expression.add("(");
expression.add("a");
expression.add("+");
expression.add("b");
expression.add("*");
expression.add("c");
expression.add("+");
expression.add("d");
expression.add(")");
expression.add("+");
expression.add("e");
expression.add(")");
expression.add("*");
expression.add("f");
}
//中缀表达式转后缀表达式
// ((a+b*c+d)+e)*f
// abc*+d+e+f*
public void convert() {
s1.clear();
s2.clear();
//将中缀表达式中的元素逐个输出
for (Object element : expression)
push(element);
//将运算符栈中的剩余元素全部输出
while (!s2.isEmpty()) {
Object top = s2.pop();
s1.addLast(top);
}
//打印后缀表达式
while (!s1.isEmpty()) {
Object top = s1.pop();
System.out.print(top);
}
}
//输出中缀表达式中的元素逐个输出,输出规则为:
//1. 创建两个栈,S1用来存输出元素,S2用来存运算符
//2. 从中缀表达式栈顶开始,向栈尾逐个读取元素
//3. 如果读到操作数,直接加到S1栈尾
//4. 如果读到左括号,则直接压入S2栈顶
//5. 如果读到运算符,且S2栈为空或S2栈顶元素为左括号,则直接压入S2栈顶
//6. 如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级大于栈顶元素,则将当前运算符压入S2栈顶
//7. 如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级小于等于栈顶元素,则将S2栈顶运算符弹出,压入S1栈顶(递归)
//8. 如果读到右括号,则将S2内首个左括号以上的运算符,全部压入S1栈顶
public void push(Object element) {
//取出S2栈顶元素,如果为空,则其type为-1
Object top = s2.peekFirst();
//如果读到操作数,直接加到S1栈尾
if (type(element) == 1) {
s1.addLast(element);
return;
}
//如果读到左括号,则直接压入S2栈顶
if (type(element) == 3) {
s2.push(element);
return;
}
//如果读到运算符,且S2栈为空或S2栈顶元素为左括号,则直接压入S2栈顶
if (type(element) == 2 && (s2.isEmpty() || type(top) == 3)) {
s2.push(element);
return;
}
//如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级大于栈顶元素,则将当前运算符压入S2栈顶
if (type(element) == 2 && type(top) == 2 && priority(element) > priority(top)) {
s2.push(element);
return;
}
//如果读到运算符,且S2栈顶也为运算符,且当前运算符优先级小于等于栈顶元素,则将S2栈顶运算符弹出,加到S1栈尾(递归)
if (type(element) == 2 && type(top) == 2 && priority(element) <= priority(top)) {
s2.pop();
s1.addLast(top);
push(element);
return;
}
//如果读到右括号,则将S2内首个左括号以上的运算符,全部加到S1栈尾
if (type(element) == 4) {
while (true) {
top = s2.pop();
if (type(top) == 3)
break;
s1.addLast(top);
}
return;
}
}
//判断元素类型
//1.操作数 2.运算符 3.左括号 4.右括号
public int type(Object element) {
if (element == null)
return -1;
if (element.equals("+"))
return 2;
if (element.equals("-"))
return 2;
if (element.equals("*"))
return 2;
if (element.equals("/"))
return 2;
if (element.equals("("))
return 3;
if (element.equals(")"))
return 4;
return 1;
}
//判断运算符优先级
public int priority(Object element) {
if (element.equals("+"))
return 1;
if (element.equals("-"))
return 1;
if (element.equals("*"))
return 2;
if (element.equals("/"))
return 2;
throw new RuntimeException("unknown operator");
}
public static void main(String[] args) {
Demo demo = new Demo();
demo.createExpression();
demo.convert();
}
}
到了这里,关于【数据结构与算法】【12】前缀表达式、中缀表达式、后缀表达式的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!