1. 前言
最近遇到了一些涉及惯性张量的实际问题,比如:
- 对两个通过铰链连接在一起的杆,如何计算整体的惯性张量?
- 对于一个由多个简单部件组合成的系统,如何计算整体的惯性张量?
在网上查找计算方法的过程中,难以通过正确的关键词找到简明的数学方法。因此我在多番查阅后,对查找到的资料做一个归纳总结,作为对《机器人学导论》书中相关章节的补充。
以下内容的符号表示将依照《机器人学导论》的命名规范。
2. 惯性张量的概念
对三维空间中的六自由度刚体而言,可能存在无穷旋转轴,对刚体而言,当其绕任意轴旋转时,我们需要一种通用的能够表征刚体质量分布的方式,因此引入惯性张量。
下面是百度百科给出的惯性张量的定义
更详细的介绍可以参见wiki Moment of inertia
为了方便起见,刚体的惯性张量的坐标系通常以刚体质心为原点,在下面的推导与证明中,我们也将遵循这一点。
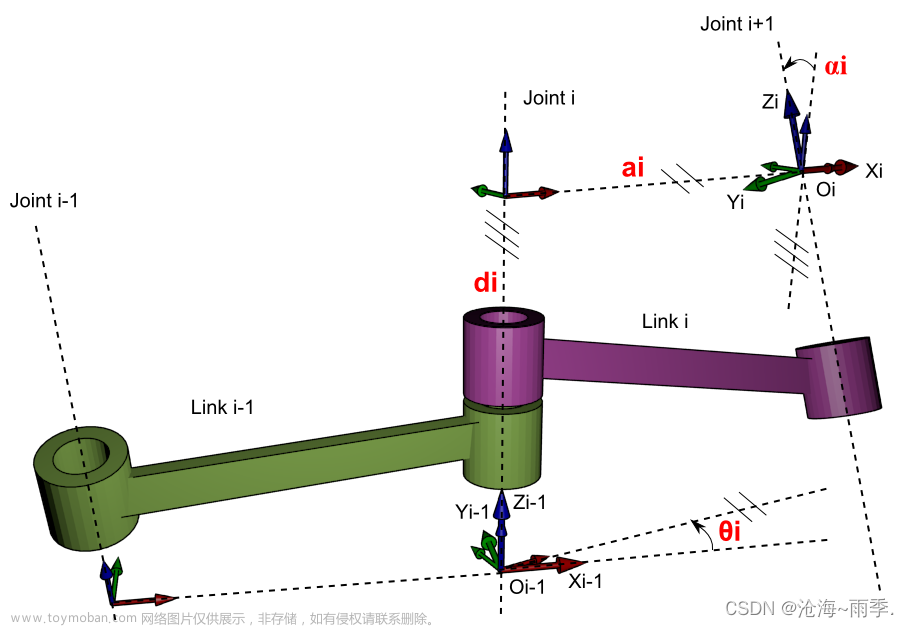
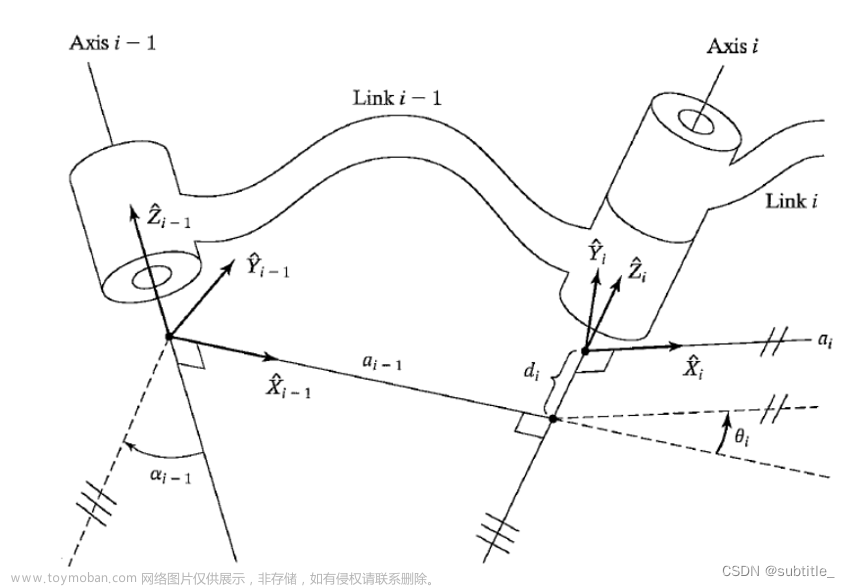
3. 惯性张量的旋转变换
设有一坐标系为 { 0 } \{0\} {0},设有一刚体,在其上选一点建立随体坐标系 { b } \{b\} {b},该刚体以 ω \omega ω 的角速度(在 { 0 } \{0\} {0}系下描述)相对 { 0 } \{0\} {0}系运动。
3.1 结论
b
I
=
(
b
0
R
T
)
(
0
I
)
(
b
0
R
)
0
I
=
(
b
0
R
)
(
b
I
)
(
b
0
R
T
)
{}^b\!I=({}^{\color{red}0}_b\!R^{\color{red}T})({}^{\color{red}0}\!I)({}^{\color{red}0}_b\!R) \\ {}^0\!I=({}^{\color{red}0}_b\!R)({}^{\color{red}b}I)({}^{\color{red}0}_b\!R^{\color{red}T})
bI=(b0RT)(0I)(b0R)0I=(b0R)(bI)(b0RT)
(红字表示:注意上标!)
3.2 证明
刚体转动能量公式(类似于平动的动能)如下:
T
=
1
2
ω
T
I
ω
\begin{equation} T=\frac{1}{2}\omega^TI\omega \end{equation}
T=21ωTIω
其中,
T
T
T 表示动能,为标量。 公式
(
1
)
(1)
(1)证明过程可参考: 刚体转动能量公式证明
容易理解,不管惯性张量、角速度在什么坐标系下表示,刚体转动的动能这个标量是一样的。因此有:
T
=
1
2
(
0
ω
T
)
(
0
I
)
(
0
ω
)
T
=
1
2
(
b
ω
T
)
(
b
I
)
(
b
ω
)
\begin{align} T&=\frac{1}{2}({}^0\omega^T)({}^0\!I)({}^0\omega) \\ T&=\frac{1}{2}({}^b\omega^T){\color{red}({}^b\!I)}({}^b\omega) \end{align}
TT=21(0ωT)(0I)(0ω)=21(bωT)(bI)(bω)
(
2
)
(2)
(2)式=
(
3
)
(3)
(3)式,
(
3
)
(3)
(3)式中为什么标红了一部分呢?马上就会用到!
将
(
2
)
(2)
(2) 式作如下展开:
T
=
1
2
(
0
ω
T
)
(
0
I
)
(
0
ω
)
=
1
2
(
b
0
R
b
ω
)
T
(
0
I
)
(
b
0
R
b
ω
)
=
1
2
(
b
ω
T
)
(
b
0
R
T
)
(
0
I
)
(
b
0
R
)
(
b
ω
)
\begin{align} T&=\frac{1}{2}({}^0\omega^T)({}^0\!I)({}^0\omega) \\ &=\frac{1}{2}({}^0_b\!R{}^b\omega)^T({}^0\!I)({}^0_b\!R{}^b\omega) \\ &=\frac{1}{2}({}^b\omega^T){\color{red}({}^0_b\!R^T)({}^0\!I)({}^0_b\!R)}({}^b\omega) \end{align}
T=21(0ωT)(0I)(0ω)=21(b0Rbω)T(0I)(b0Rbω)=21(bωT)(b0RT)(0I)(b0R)(bω)
(
4
)
−
(
6
)
(4)-(6)
(4)−(6)式的推导主要是:旋转矩阵变换+结合律,对比
(
3
)
(3)
(3)和
(
6
)
(6)
(6)式有:
b
I
=
(
b
0
R
T
)
(
0
I
)
(
b
0
R
)
\begin{equation} {}^b\!I=({}^{\color{red}0}_b\!R^{\color{red}T})({}^{\color{red}0}\!I)({}^{\color{red}0}_b\!R) \end{equation}
bI=(b0RT)(0I)(b0R)
(
7
)
(7)
(7)式即为惯性张量的旋转变换公式
进一步,
(
7
)
(7)
(7)式两边左乘
(
b
0
R
)
({}^{\color{red}0}_b\!R)
(b0R),右乘
(
b
0
R
T
)
({}^{\color{red}0}_b\!R^{\color{red}T})
(b0RT),可得:
0
I
=
(
b
0
R
)
(
b
I
)
(
b
0
R
T
)
\begin{align} {}^0\!I=({}^{\color{red}0}_b\!R)({}^{\color{red}b}I)({}^{\color{red}0}_b\!R^{\color{red}T}) \end{align}
0I=(b0R)(bI)(b0RT)
4. 惯性张量的平移变换
设有一质量为 m m m 的刚体,在其上选一点建立随体坐标系 { C } \{C\} {C},已知另一坐标系 { A } \{A\} {A}与 { C } \{C\} {C}系为平移关系,且 { C } \{C\} {C}系原点在 { A } \{A\} {A}系中的位置为 P c P_c Pc。
4.1 结论
刚体在
{
A
}
\{A\}
{A}系中的惯性张量可写为:
A
I
=
C
I
+
m
(
P
c
T
P
c
I
3
−
P
c
P
c
T
)
{}^A\!I={}^C\!I+m(P_c^TP_cI_3 - P_cP_c^T)
AI=CI+m(PcTPcI3−PcPcT)
其中
I
3
I_3
I3 是
3
×
3
3\times3
3×3 的单位矩阵。
上式为《机器人学导论》的结论,与下面维基百科给出的公式一致,可以理解为平行轴定理的推广。
4.2 证明
下面是维基百科关于张量平行轴定理的介绍:
更详细的证明可以参考知网的这篇文章:惯性张量平移和旋转复合变换的一般形式及其应用文章来源:https://www.toymoban.com/news/detail-719245.html
参考资料
[1] 机器人学导论(原书第四版) John J.Craig著,贠超 王超译
[2] 惯性张量平移和旋转复合变换的一般形式及其应用
[3] Parallel axis theorem文章来源地址https://www.toymoban.com/news/detail-719245.html
到了这里,关于【机器人学导论】惯性张量旋转和平移变换的推导的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!