数据结构与算法-二叉树的遍历-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构与算法-二叉树的遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构与算法-二叉树的遍历,初阶数据结构与算法,数据结构,算法,c++,链表
🌞 “少年没有乌托邦，心向远方自明朗！”

🎈1.二叉树的遍历

二叉树的遍历是按照一定次序访问二叉树中的所有结点，且每个结点仅被访问一次的过程。遍历线性结构是容易解决的，而二叉树的结构是非线性结构，需要寻找规律，使二叉树的结点排列在一个线性队列上，便于遍历。

由二叉树的递归定义知，二叉树有根结点、左子树和右子树3个基本单元组成。如果以L、D、R分别表示遍历左子树、遍历根结点和遍历右子树，则遍历整个二叉树有DLR、LDR、LRD、DRL、RDL、RLD六种遍历方案。若规定先左后右，则只有DLR、LDR、LRD三种遍历方案，分别称为先序遍历、中序遍历和后序遍历。

🔭1.1先序遍历

🔎先序遍历二叉树的过程如下：

访问根结点
先序遍历左子树
先序遍历右子树

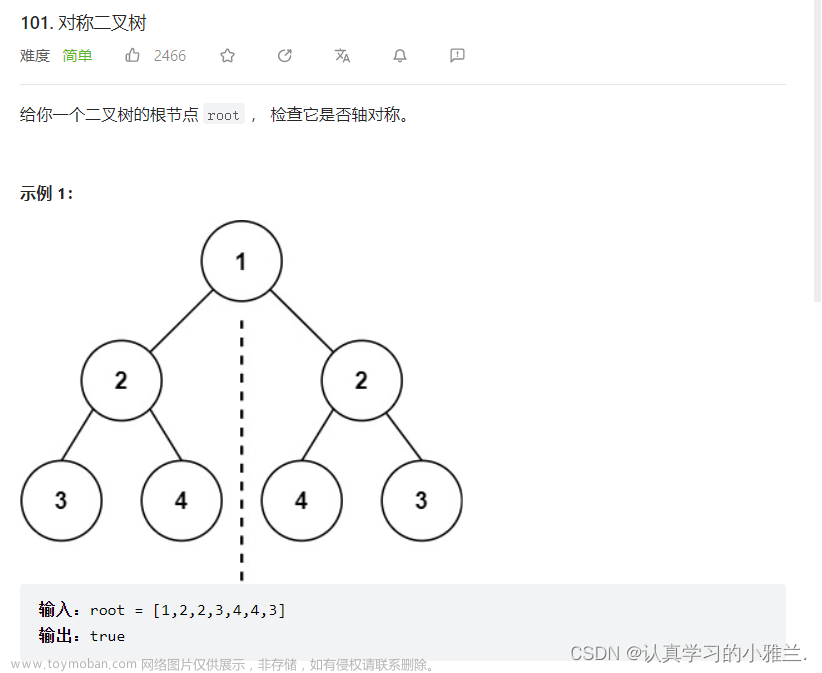
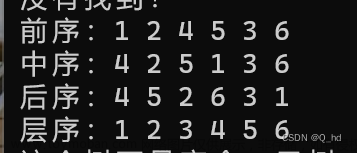
✅ 如下图所示二叉树的先序序列为：ABJDGCEHF
数据结构与算法-二叉树的遍历,初阶数据结构与算法,数据结构,算法,c++,链表

🔭1.2中序遍历

🔎中序遍历二叉树的过程如下：

中序遍历左子树
访问根结点
中序遍历右子树

✅ 如下图所示二叉树的中序序列为：JBGDAEHCF
数据结构与算法-二叉树的遍历,初阶数据结构与算法,数据结构,算法,c++,链表

🔭1.3后序遍历

🔎后序遍历二叉树的过程如下：

后序遍历左子树
后序遍历右子树
访问根结点

✅ 如下图所示二叉树的后序序列为：JGDBHEFCA
数据结构与算法-二叉树的遍历,初阶数据结构与算法,数据结构,算法,c++,链表

🔭1.4层次遍历

🔎二叉树非空（设二叉树的高度为h时），层次遍历二叉树的过程如下：

先访问根结点（第1层）
再从左向右访问每层结点

✅ 如下图所示二叉树的层次序列为：ABCJDEFGH
数据结构与算法-二叉树的遍历,初阶数据结构与算法,数据结构,算法,c++,链表

🔭1.5二叉树遍历的递归算法

📝1.5.1先序遍历

void BiTree::InTraverse(BitNode* t)
{
	//先序遍历递归函数
	if (t)
	{
	    cout << data;
		InTraverse(t->lchild);
		InTraverse(t->rchild);
	}
}
void BiTree::InTraverseBiTree()
{
	BitNode* p = bt;
	InTraverse(p);
}

📝1.5.2中序遍历

void BiTree::InTraverse(BitNode* t)
{
	//中序遍历递归函数
	if (t)
	{
		InTraverse(t->lchild);
		cout << data;
		InTraverse(t->rchild);
	}
}
void BiTree::InTraverseBiTree()
{
	BitNode* p = bt;
	InTraverse(p);
}

📝1.5.3后序遍历

void BiTree::InTraverse(BitNode* t)
{
	//中序遍历递归函数
	if (t)
	{
		InTraverse(t->lchild);
		InTraverse(t->rchild);
		cout << data;
	}
}
void BiTree::InTraverseBiTree()
{
	BitNode* p = bt;
	InTraverse(p);
}

📝1.5.4例题一

已知二叉树采用二叉链表存储结构存储，设计一个交换二叉树左右子树的递归算法。

void ChangeSubTree(BitNode*& t)
{
	BitNode* temp;
	if (t)
	{
		temp = new BitNode;
		temp = t->lchild;
		t->lchild = t->rchild;
		t->rchild = temp;
		ChangeSubTree(t->lchild);
		ChangeSubTree(t->rchild);
	}
}

📝1.5.5例题二

已知二叉树采用二叉链表结构存储，请设计一个判断两棵二叉树是否相似的算法。若相似返回1，否则返回0.所谓两棵二叉树s和t相似是指s和t均为空的二叉树；或者s和t的根结点相似（值可以不同），且左右子树分别相似。

int Alike(BitNode* s, BitTree* t)
{
	if (s == NULL && t == NULL)
		return 1;
	else if (s == NULL || t == NULL)
		return 0;
	else
		return Alike(s->lchild, t->lchild) && Alike(s->rchild, t->rchild);
}

📝1.5.6例题三

已知二叉树采用二叉链表存储结构存储，设计一个将二叉树s拷贝给t的递归算法。

void CopyBitree(BitNode* s, BitNode*& t)
{
	if (s == NULL)
		t = NULL;
	else
	{
		t = new BitNode;
		t->data = s->data;
		CopyBiTree(s->lchild, t->lchild);
		CopyBiTree(s->rchild, t->rchild);
	}
}

🔭1.6二叉树遍历的非递归算法

为了把递归过程改成一个非递归过程，需要利用一个工作栈，记录遍历时的回退路径。

🔎先序遍历的算法流程：

用指针p指向当前需要处理的结点
访问该结点，该结点入栈，并将p指向左孩子，循环处理左子树
当该结点无左孩子时，表示栈顶结点无左子树，栈顶结点退栈，并将p指向刚出栈结点的右孩子
对右子树进行相同处理
重复上述过程，直到栈为空为止

void PreTraverse(BitNode* t)
{
	BitNode* p = t;
	SqStack s;
	while (p || !s.EmptyStack())
	{
		if (p)
		{//访问根结点，根结点指针入栈，遍历左子树
			cout << p->data;//访问结点
			s.Push(p);
			p = p->lchild;
		}
		else
		{//根结点退栈，遍历右子树
			s.Pop(p);
			p = p->rchild;
		}
	}
}

🔎中序遍历的算法流程：

用指针p指向当前需要处理的结点，p入栈
扫描该结点的左子树上的所有结点并将它们一一进栈
当该结点无左孩子时，表示栈顶结点无左子树，栈顶结点退栈，该问该结点，并将p指向刚出栈结点的右孩子
对右子树进行相同处理
重复上述过程，直到栈为空为止

void PreTraverse(BitNode* t)
{
	BitNode* p = t;
	SqStack s;
	while (p || !s.EmptyStack())
	{
		if (p)
		{//根结点入栈，遍历左子树
			s.Push(p);
			p = p->lchild;
		}
		else
		{//根结点退栈，访问结点，遍历右子树
			s.Pop(p);
			cout << p->data;//访问结点
			p = p->rchild;
		}
	}
}

🔎后序遍历的算法流程：

用指针p指向当前需要处理的结点，并置标志位flag=0（表示第一次入栈），p入栈
扫描该结点的左子树上的所有结点并将它们一一进栈
当该结点无左孩子时，表示栈顶结点无左子树，栈顶结点退栈，并判断标志位的值，若flag=0，置flag=1（表示该结点第二次入栈），该问该结点，并将p指向刚出栈结点的右孩子，若flag=1,则访问该结点，置p = NULL.
对右子树进行相同处理
重复上述过程，直到栈为空为止

typedef struct 
{
	BitNode* pointer;
	int flag;
}BitNodeFlag;
void PostTraverse(BitNode* t)
{
	BitNodeFlag bf;
	BitNode* p = t;
	SqStack s;
	while (p || !s.EmptyStack())
	{
		if (p)
		{
			bf.pointer = p;
			bf.flag = 0;
			s.Push(bf);
			p = p->lchild;
		}
		else
		{
			s.Pop(bf);
			if (bf.flag == 0)
			{
				bf.uflag = 1;
				s.Push(bf);
				p = p->rchild;
			}
			else
			{
				cout << bf.pointer->data;
				p = NULL;
			}
		}
	}
}

🔎层次遍历的算法流程：

层次遍历访问完某一层的结点后，再按照它们的访问次序对各结点的左、右子树顺序访问。如此一层一层地访问，先访问的结点其左、右孩子也要先访问。层次遍历过程可以用队列来实现。

void LevelTraverse(BitNode* t)
{
	BitNode* p = t;
	LinkQueue q;//初始化建立空队列
	if (p)
		q.Enqueue(p);//根结点入队
	while (!q.EmptyQueue())
	{
		q.DeQueue(p);//出队
		cout << p->data;//访问结点
		if (p->lchild)
			q.EnQueue(p->lchild);//左子树根结点入队
		if (p->rchild)
			q.EnQueue(p->rchild);//右子树根结点入队
	}
}

🔭1.7例题四

已知二叉树采用二叉链表存储结构存储，设计一个计算二叉树叶子结点的非递归算法。

int CountBitLeaf(BitNode* t)
{
	SqStack s;
	BitNode* p = t;
	int count = 0;
	while (p != NULL || !s.EmptyStack())
	{
		while (p != NULL)
		{
			s.Push(p);
			p = p->lchild;
		}
		if (!s.EmptyStack())
		{
			s.Pop(p);
			if (p->lchild == NULL && p->rchild == NULL)
				count++；
				p = p->rchild;
		}
	}
	return count;
}