二叉搜索树的实现（递归方式）

这篇具有很好参考价值的文章主要介绍了二叉搜索树的实现（递归方式）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

实现思路

插入操作

删除操作

完整代码

测试案例

总结

二叉搜索树（Binary Search Tree，BST）是一种常用的数据结构，它具有以下特点：

左子树上所有节点的值均小于它的根节点的值
右子树上所有节点的值均大于它的根节点的值
左右子树也分别为二叉搜索树

在实际应用中，BST被广泛使用，例如在数据库中的索引、哈希表等。

本文将介绍如何使用递归的方式实现BST，并提供完整代码和测试案例。

实现思路

BST的基本操作包括查找、插入和删除。这里我们只讲解递归方式实现BST的插入和删除操作。

插入操作

插入操作可以分为两种方式：

版本一：传入父节点，通过比较key值大小，递归向下寻找插入位置。
版本二：使用引用，第一步传参时，root是_root的别名；递归过程中，root是父节点指向它的指针的别名，修改root就是修改了父节点的连接。

版本二的实现方式更加简洁，因此我们选择使用版本二来实现插入操作。

删除操作

删除操作也可以分为两种方式：

版本一：传入父节点，通过比较key值大小，递归向下寻找删除节点。
版本二：使用引用，第一步传参时，root是_root的别名；递归过程中，root是父节点_left或·_right的别名，修改root就是修改了父节点的连接。

版本二同样更加简洁，因此我们选择使用版本二来实现删除操作。需要注意的是，当删除节点有两个子节点时，需要先找到其左子树中最大的节点或右子树中最小的节点，将其值替换到要删除的节点上，再删除左子树中最大的节点或右子树中最小的节点。

无论是查找、插入、删除，如果使用递归，都需要传参根节点，通过根节点来递归处理子问题，但是在类的实现中，成员变量根节点_root是私有变量，在类外无法访问，针对这种问题，C++常见的处理方式就是套用一层接口函数，定义对应功能的私有函数提供给接口函数调用；用户直接调用接口函数，和之前没有区别，接口函数内再调用对应功能的私有函数，私有函数只在类中使用，自然就可以调用BST的私有成员_root。

完整代码

#include<iostream>
using namespace std;

template <class K>
class BSTreeNode
{
public:
    BSTreeNode<K>* _left;
    BSTreeNode<K>* _right;
    K _key;

    BSTreeNode(const K& key)
        :_left(nullptr)
        , _right(nullptr)
        , _key(key)
    { }
};

template<class K>
class BSTree
{
    typedef BSTreeNode<K> Node;
public:
    bool Find(const K& key)
    {
        return _Find(_root, key);
    }

    bool Insert(const K& key)
    {
        return _Insert2(_root, key);
    }

    void midOrder()
    {
        _midOrder(_root);
    }

    bool Erase(const K& key)
    {
        return _Erase(_root, key);
    }
private:
    Node* _root = nullptr;

    bool _Find(Node* root, const K& key)
    {
        if (root == nullptr)
            return false;

        if (key < root->_key)
        {
            return _Find(root->_left, key);
        }
        else if (key > root->_key)
        {
            return _Find(root->_right, key);
        }
        else
        {
            return true;
        }
    }

    void _midOrder(Node* root)
    {
        if (root == nullptr)
            return;

        _midOrder(root->_left);
        cout << root->_key << " ";
        _midOrder(root->_right);
    }

    bool _Insert2(Node*& root, const K& key)
    {
        if (root == nullptr)
        {
            root = new Node(key);
            return true;
        }

        if (key < root->_key)
            return _Insert2(root->_left, key);
        else if (key > root->_key)
            return _Insert2(root->_right, key);
        else
            return false;
    }

    bool _Erase(Node*& root, const K& key)
    {
        if (root == nullptr)
            return false;

        if (key < root->_key)
            return _Erase(root->_left, key);
        else if (key > root->_key)
            return _Erase(root->_right, key);
        else
        {
            if (root->_left == nullptr)
            {
                Node* del = root;
                root = root->_right;
                delete del;
            }
            else if (root->_right == nullptr)
            {
                Node* del = root;
                root = root->_left;
                delete del;
            }
            else
            {
                //要删除的节点有两个子节点，替换法
				//先找到一个合适的替换节点，然后把值替换
				//合适的替换节点绝对是上面的几种情况：只有左子树、只有右子树、没有子节点
				Node* subRight = root->_left;
				while (subRight->_right)
				{
					subRight = subRight->_right;
				}
				swap(root->_key, subRight->_key);

				//交换值后，目前虽然整棵树不是搜索二叉树，但是root的左右子树都还是BST，递归去删除即可
				return _Erase(root->_left, key);
            }
        }
        return true;
    }
};

int main()
{
    int a[] = { 8,3,1,6,4,7,14,13 };
    BSTree<int> bst;
    for (int x : a)
    {
        bst.Insert(x);
    }
    bst.midOrder();

    //测试：遍历删除
    for (int x : a)
    {
        bst.midOrder();
        cout << endl;
        bst.Erase(x);
        bst.midOrder();
        cout << endl;
        cout << endl;
    }

    cout << "全部删除成功" << endl;
    system("pause");
    return 0;
}

测试案例

int a[] = { 8,3,1,6,4,7,14,13 };
BSTree<int> bst;
for (int x : a)
{
    bst.Insert(x);
}
bst.midOrder();

//测试：遍历删除
for (int x : a)
{
    bst.midOrder();
    cout << endl;
    bst.Erase(x);
    bst.midOrder();
    cout << endl;
    cout << endl;
}

cout << "全部删除成功" << endl;

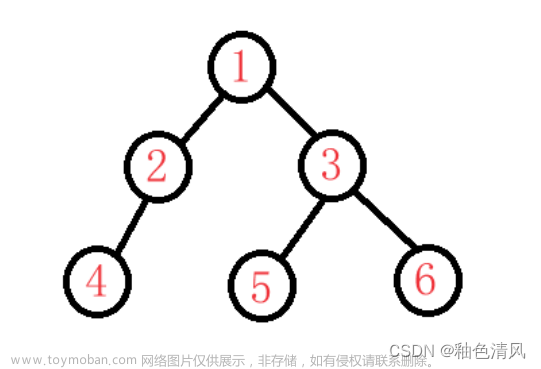
构建的二叉树如下：

二叉搜索树的实现（递归方式）,数据结构与算法,C/C++,c++,算法,开发语言,数据结构

运行结果如下：

1 3 4 6 7 8 13 14 
1 3 4 6 7 8 13 14 
1 3 4 6 7 8 13 14 

1 3 4 6 7 13 14 
1 3 4 6 7 13 14 
1 3 4 6 7 13 14 

1 3 4 6 13 14 
1 3 4 6 13 14 
1 3 4 6 13 14 

1 3 4 6 13 
1 3 4 6 13 
1 3 4 6 13 

1 3 4 6 
1 3 4 6 
1 3 4 6 

1 3 4 
1 3 4 
1 3 4 

1 3 
1 3 
1 3 

1 
1 
1 

全部删除成功

总结

本文介绍了使用递归的方式实现BST的插入和删除操作，并提供了完整代码和测试案例。递归虽然简洁，但需要注意递归边界条件、参数传递方式等问题。在实际应用中，也可以使用迭代的方式实现BST的基本操作。文章来源地址https://www.toymoban.com/news/detail-719928.html

到了这里，关于二叉搜索树的实现（递归方式）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！