Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码)-Toy模板网

这篇具有很好参考价值的文章主要介绍了Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、实验要求

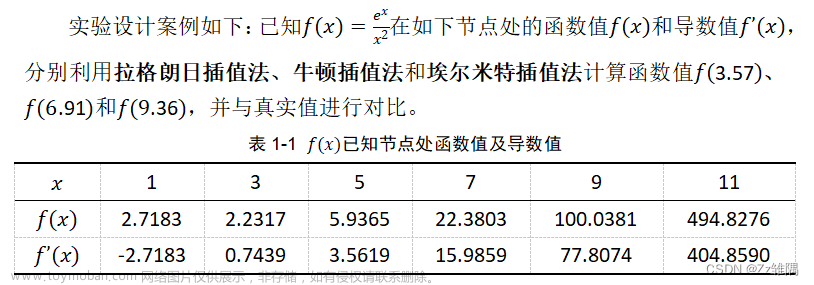
已知函数表：
Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码),matlab,开发语言
求出Lagrange 插值多项式，并计算x=1.2处的y的近似值。

二、MATLAB代码

求解多项式：

X = input('请输入横坐标向量X:\nX=');  % 获取用户输入的横坐标向量
Y = input('请输入纵坐标向量Y:\nY=');  % 获取用户输入的纵坐标向量
m = length(X);  % 获取节点个数
L = ones(m, m);  % 初始化基函数系数矩阵
for k = 1 : m  % 循环计算每个基函数的系数
    V = 1;  % 初始化基函数的临时变量
    for i = 1 : m
        if k ~= i  % 排除当前节点时的计算
            V = conv(V, poly(X(i))) / (X(k) - X(i));  % 在当前节点处计算基函数的系数
        end
    end
    L(k, :) = V;  % 将基函数的系数存储到矩阵中
end
l = sym(zeros(m, 1));  % 初始化基函数数组
for k = 1 : m  % 遍历基函数系数矩阵
    l(k) = poly2sym(L(k, :));  % 将基函数系数转化为符号表达式
end
fprintf('基函数为：\n');
for k = 1 : m  % 输出每个基函数的表达式
    fprintf('q%d(x)=%s\n', k, char(l(k)));
end
P = sym(0);  % 初始化拉格朗日多项式
for k = 1 : m  % 计算拉格朗日多项式的表达式
    P = P + Y(k) * l(k);
end
fprintf('拉格朗日多项式为：\nP(x)=%s\n', char(P));  % 输出拉格朗日多项式的表达式

求解近似值：

% 定义拉格朗日插值多项式的系数
coeff = [1/12, -29/6, 1/12, 62/3];

% 计算 x=1.2 处的 y 的近似值
x = 1.2;
y_approx = polyval(coeff, x);

% 显示结果
disp(['当 x = ' num2str(x) ' 时，y 的近似值为 ' num2str(y_approx)]);

三、实验结果

请输入横坐标向量X:
X=[1, 2, 4, 5]
请输入纵坐标向量Y:
Y=[16,12,8,9]
基函数为：
q1(x)=(11x^2)/12 - (19x)/6 - x^3/12 + 10/3
q2(x)=(29x)/6 - (5x^2)/3 + x^3/6 - 10/3
q3(x)=(4x^2)/3 - (17x)/6 - x^3/6 + 5/3
q4(x)=(7x)/6 - (7x^2)/12 + x^3/12 - 2/3
拉格朗日多项式为：
P(x)=x^2/12 - (29*x)/6 + x^3/12 + 62/3
Lagrange插值法实验:求拉格朗日插值多项式和对应x的近似值matlab实现(内附代码),matlab,开发语言
当 x = 1.2 时，y 的近似值为 13.9507