重温数据结构与算法之约瑟夫问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了重温数据结构与算法之约瑟夫问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

数据结构约瑟夫问题总结,java,leetcode,链表,数据结构,约瑟夫环,约瑟夫问题,动态规划

前言

约瑟夫问题，是一个计算机科学和数学中的问题，在计算机编程的算法中，类似问题又称为约瑟夫环，又称“丢手绢问题”。

据说著名犹太历史学家 Josephus 有过以下的故事：

在罗马人占领乔塔帕特后，39个犹太人与Josephus及他的朋友躲到一个洞中，39个犹太人决定宁愿死也不要被敌人抓到，于是决定了一个自杀方式，41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。

然而 Josephus 和他的朋友并不想遵从这个规则，Josephus 要他的朋友先假装遵从，他将朋友与自己安排在第16个与第31个位置，于是逃过了这场死亡游戏。

一、暴力法

可以使用暴力法模拟整个过程:

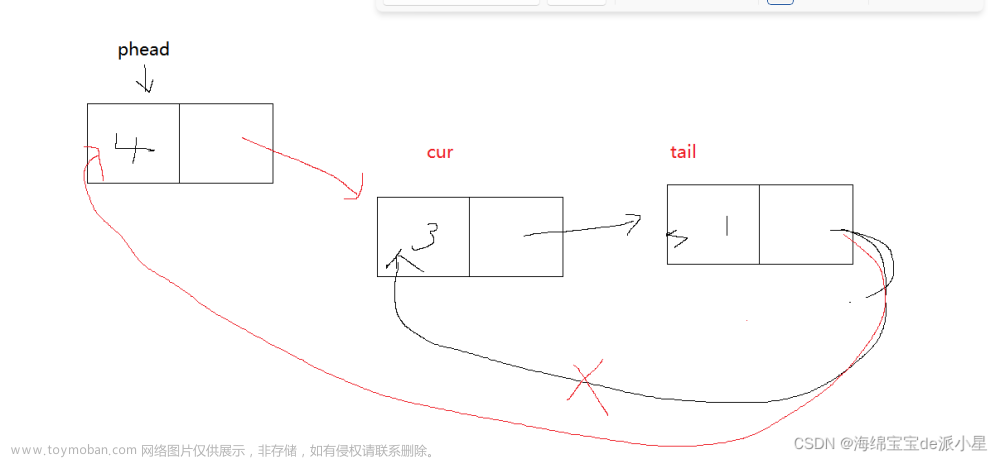
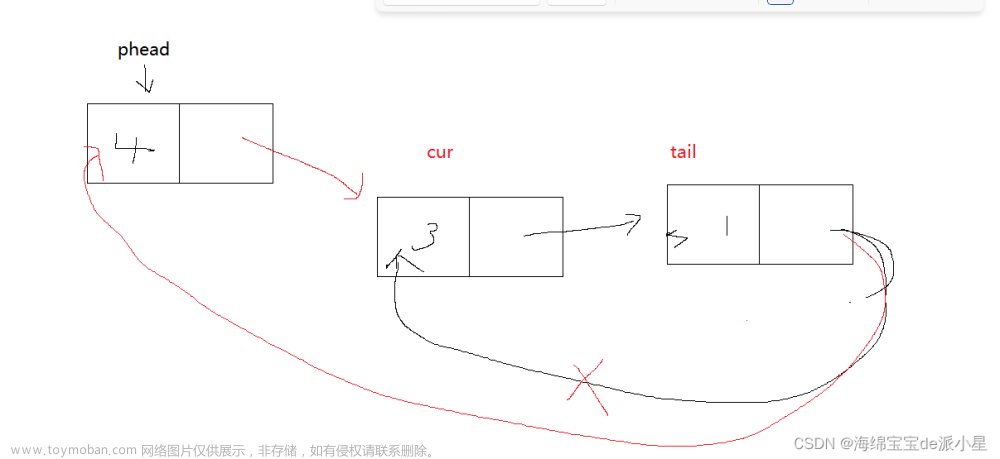
首先自定义一个循环链表，需要将末尾节点的 next 指针指向首节点
n(= 41) 个人编号从 0-40，添加到链表中
删除节点需要一个前置节点 pre ，和一个要删除的当前节点 cur，这样删除时只需要将 pre 的 next 指向 cur 的 next 就能实现删除cur 节点
定义1个计数器变量 count 当达到 m(= 3) 时，删除节点并将计数器归0
由于最终存活2人，循环条件可以为 cur.next != pre 。如果存活1人，条件可以为 cur.next != cur。
所以最终存活编号 15 和 30，由于这个编号从 0 开始，所以 Josephus 将朋友与自己安排在第16个与第31个位置，逃过了这场死亡游戏。

class Node {
    int data;
    Node next;
}

class CycleLinkedList  {
    Node first;
    Node last;

    public void add(int o) {
        Node l = last;
        Node n = new Node();
        n.data = o;
        last = n;
        if (l == null) {
            first = n;
        } else {
            l.next = n;
        }
        last.next = first;
    }
}

public void josephus() {

    int n = 41, m = 3;
    CycleLinkedList list = new CycleLinkedList();
    for (int i = 0; i < n; i++) {
        list.add(i);
    }

    int count = 0;
    Node pre = list.first;
    Node cur = pre;
    while (cur.next != pre) {
        count++;

        if (count == m) {
            pre.next = cur.next;
            System.out.println(" killer 编号：" + cur.data);
            count = 0;
        } else {
            pre = cur;
        }
        cur = cur.next;
    }
    System.out.println("最终存活2人编号：" + cur.data + "," + pre.data);
    // 最终存活2人编号：15,30
}

二、动态规划

上述暴力法易于理解，实现简单。但是重复遍历降低效率，每删除一个元素需要移动 m 步，对于 n 个元素，时间复杂度为 $O (mn)$ 。

其实可以发现上述问题其实满足动态规划的解决范畴。每一步求编号就是子问题，上一步求得的编号对下一步有帮助。那么 dp 重要的三部分如下：

状态定义：dp[i] 表示约瑟夫问题的解，即 i 个元素每 m 个删去，最终留下元素的编号
转移方程推导：
- $\underbrace{0,1,\cdots, i-2}_{\text{i-1个}}$ 得到最终元素编号为 $d p [i - 1]$
- 那么 $\underbrace{0,1,\cdots,k-1,k,k+1,\cdots, i-1}_{\text{i个}}$ 去掉第一个 $1)\%i = k$ 后(存在m大于i的情况，需要取余)，剩下 $\underbrace{k+1,k+2,\cdots,i-2,i-1,0,1,\cdots,k-1}_{\text{i-1个}}$ ，元素数量也变为 $i - 1$ 个，由于元素顺序是递增而且是环状的，到达最大又会从最小开始，可以等价到上述从 $0$ 开始到 $i - 2$ 的数字序列。
- 得到 $d p [i - 1]$ 的数字序列是从0开始，那么可以推导 $d p [i]$ 了，为 $\% i$ ， $1)\%i + 1 + dp[i - 1] ) \% i$
- 所以最终推导方程为: $\% i$
初始状态：dp[1]=0 表示 1个元素最终留下元素的编号为0

public void josephus1() {

    int n = 41, m = 3;
    int [] dp = new int[n + 1];
    dp[1] = 0;
    for (int i = 2; i < n + 1; i++) {
        dp[i] = (dp[i - 1] + m) % i;
    }
    System.out.println(dp[n]);
}

// 上述dp数组可用变量替代
public void josephus2() {

    int n = 41, m = 3;
    int start = 0;
    for (int i = 2; i < n + 1; i++) {
        start = (start + m) % i;
    }
    System.out.println(start);
}

上述使用动态规划可以求出最后存活人的编号，而且时间复杂度为 $O (n)$ ，使用上述代码有个问题就是不能得到倒数第2个人的编号，dp[n-1]是40个人最后存活人的编号。其实也可以利用 dp 的思想求倒数第二个人的编号。

状态定义：dp[i] 表示 i 个元素每 m 个删去，倒数第 2 个留下元素的编号
状态转移方程：和上面一样， $\% i$
初始状态：dp[2] = (m + 1) % 2

int n = 41, m = 3;
int start = (m + 1) % 2;
for (int i = 3; i < n + 1; i++) {
    start = (start + m) % i;
}
System.out.println(start);

三、实战

3.1 力扣 1823. 找出游戏的获胜者

https://leetcode.cn/problems/find-the-winner-of-the-circular-game/

共有 n 名小伙伴一起做游戏。小伙伴们围成一圈，按顺时针顺序从 1 到 n 编号。确切地说，从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置，其中 1 <= i < n ，从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。

游戏遵循如下规则：
从第 1 名小伙伴所在位置 开始 。
沿着顺时针方向数 k 名小伙伴，计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数，一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子，并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴，从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始，回到步骤 2 继续执行。
否则，圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ，和一个整数 k ，返回游戏的获胜者。

经典的约瑟夫环问题，不过换了个说法

public int findTheWinner(int n, int k) {
	int start = 0;
    for (int i = 2; i < n + 1; i++) {
        start = (start + k) % i;
    }
    return start + 1;
}

3.2 洛谷 P1996 约瑟夫问题

https://www.luogu.com.cn/problem/P1996

n 个人围成一圈，从第一个人开始报数,数到 m 的人出列，再由下一个人重新从 1 开始报数，数到 m 的人再出圈，依次类推，直到所有的人都出圈，请输出依次出圈人的编号。

这里要依次求出圈人的编号, 可以使用暴力法。文章来源地址https://www.toymoban.com/news/detail-720501.html

import java.io.*;
import java.util.*;
public class Main {
    static class Node {
        int data;
        Node next;
    }

    static class CycleLinkedList  {
        Node first;
        Node last;

        public void add(int o) {
            Node l = last;
            Node n = new Node();
            n.data = o;
            last = n;
            if (l == null) {
                first = n;
            } else {
                l.next = n;
            }
            last.next = first;
        }
    }
    public static void main(String args[]) throws Exception {
        Scanner cin=new Scanner(System.in);
        int n = cin.nextInt(), m = cin.nextInt();
        int [] ans = new int[n];
        int c = 0;

        CycleLinkedList list = new CycleLinkedList();
        for (int i = 0; i < n; i++) {
            list.add(i + 1);
        }

        int count = 0;
        Node pre = list.first;
        Node cur = pre;
        while (cur.next != cur) {
            count++;

            if (count == m) {
                pre.next = cur.next;
                ans[c++] = cur.data;
                count = 0;
            } else {
                pre = cur;
            }
            cur = cur.next;
        }
        ans[c] = cur.data;
        for (int an : ans) {
            System.out.print(an + " ");
        }
    }
}