什么是采样
统计学中的采样指的是从总体中随机选择一部分样本进行观测和分析的过程。在采样过程中，要保证样本的代表性，即样本应该能够准确地反映总体的特征。
通常，采样的目的是为了对总体进行推断，比如对总体的均值、方差等参数进行估计，或者对总体分布的形态和特征进行分析。
举个例子，目前有一个随机变量X的概率密度函数为f(x),如图一。那么我们采样的过程就是，在区间[a,b]中抽取m个点，这m个点能够反映X的分布情况，当然m越大越好，即采样的点越多越好。
那么现在有一个问题，既然我们已经知道了随机变量X的分布函数f(x)，那我们直接对所有的函数都用均匀采样的方式从[a,b]中采取点不就可以了。
NoNoNo，这想法就太天真了，我举的例子当然是一个简单的分布函数，真实的情况当然有各种各样复杂的分布，比如这个图二，如果是这种分布，那你用均匀采样的方式来进行，岂不是得不到源函数f(x)的分布状况了，没法反映总体的情况。
总结一下为什么不能全部用均匀采样的原因，有如下几点：
- 高维空间下均匀采样的效率低下： 在高维空间下，数据点往往变得稀疏，因此需要更多的样本才能充分表示数据集。然而，采样点的数量随着维度的增加呈指数增长，因此在高维空间下使用均匀采样会导致采样效率低下。
- 数据分布不均匀： 在现实世界中，很多数据集的分布都是不均匀的，即某些区域的数据点比其他区域更密集。如果使用均匀采样，则无法捕捉到这些更密集的区域，因此需要更加智能的采样策略，比如在密集区域采样更多的样本。
- 特殊的数据分布形式： 在某些情况下，数据集的分布形式可能是特殊的，例如多峰分布、长尾分布等。在这种情况下，使用均匀采样可能无法捕捉到所有峰值或长尾，因此需要使用更适合数据分布形式的采样方法。
因此，为了更好地表示和理解数据集，需要根据数据集的特点选择不同的采样方法。
概率密度函数 probablity density function(PDF)
概率密度函数是用来描述连续型随机变量的概率分布的函数。它反映了随机变量在某个取值点附近的可能性，而不是在某个确定点的概率。概率密度函数 f(x) 的值并不是概率，而是在 x 处的密度。因此，概率密度函数 f(x) 的积分才是概率，即 P(a≤X≤b)=
∫
b
a
f
(
x
)
d
x
\displaystyle \int^{a}_{b}{f(x)dx}
∫baf(x)dx。如下分别是均匀分布和高斯分布的概率密度函数。
累积概率分布函数 cumulative probablity distribution function(CDF)
累积概率分布函数的取值是[0, 1], 他就是概率密度函数的积分，累积概率分布函数在a点的值，就是PDF在[ − ∞ -{\infty} −∞, a]区间内的定积分，CDF能完整描述一个实数随机变量X的概率分布。 累积概率密度函数反映了随机变量X小于等于某一值的概率。 累积概率密度函数是一个非降函数。
蒙特卡罗(Monte Carlo)
MC算法是一大类随机算法，用大量随机样本估算数据的真实值，常用来解决概率统计中的许多复杂计算问题。
蒙特卡罗应用一：求阴影部分面积
如下图，求图中阴影部分的面积
首先，我不知道阴影部分的面积怎么求，但是我知道可以用MC算法进行模拟计算。如何进行模拟，就是扔豆子，我们在这个正方形中扔n个豆子，其中有m个豆子在阴影中，那么阴影部分的面积占整个正方形面积的m/n，又因为正方形面积为4，所以阴影部分面积为4m/n。
原理很简单，MC算法本就是通过大量的实验进行模拟得出的结果，n个豆子很容易统计，那么我们如何知道豆子是否落在阴影部分中？观察可知，阴影是在圆内部的，圆的方程为：
(
x
−
1
)
2
+
(
y
−
1
)
2
<
=
1
(x-1)^2+(y-1)^2<=1
(x−1)2+(y−1)2<=1。同时还知道阴影部分是在蓝色圈住的扇形的外部，扇形的方程为：
x
2
+
y
2
<
=
2
x^2+y^2<=2
x2+y2<=2。根据上述两个条件我们可以得到，当满足该公式时，即可知道豆子是落在阴影中的：
{
(
x
−
1
)
2
+
(
y
−
1
)
2
<
=
1
x
2
+
y
2
>
2
\begin{cases} \ (x-1)^2+(y-1)^2<=1 \\ \ x^2+y^2>2 \\ \end{cases}
{ (x−1)2+(y−1)2<=1 x2+y2>2
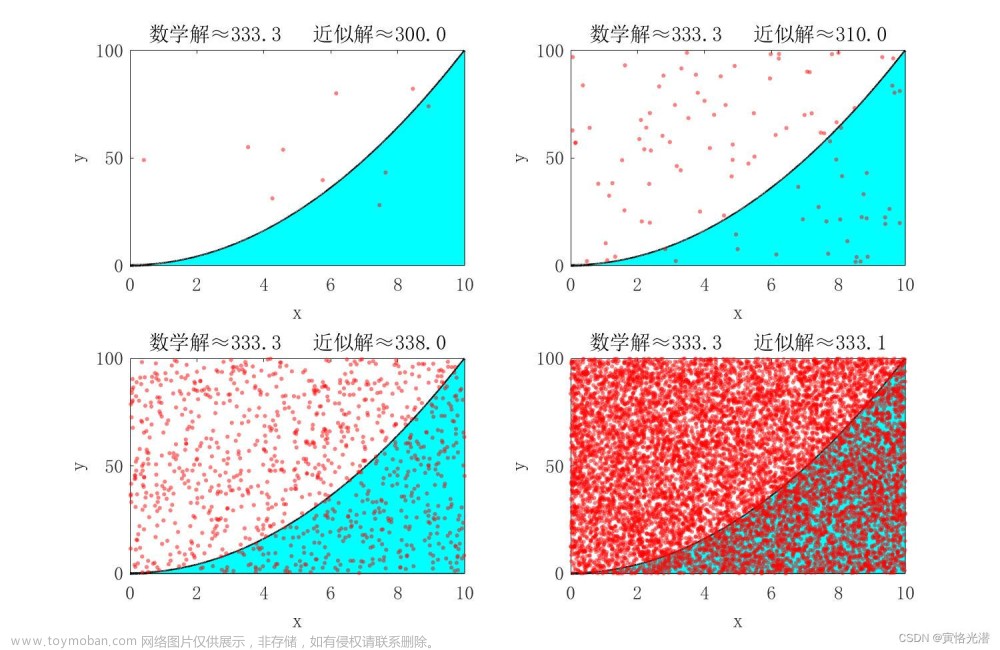
蒙特卡罗应用二：求定积分
给你一个不可求积分的单变量函数
f
(
x
)
f(x)
f(x)，求
I
=
∫
a
b
f
(
x
)
d
x
I=\int_{a}^{b} f(x)dx
I=∫abf(x)dx
这里的
f
(
x
)
f(x)
f(x)是不可积分的函数，所以直接求肯定无法求出结果，这时候我们可以用MC算法求出一个近似值。具体做法是：
- 首先，从区间[a,b]均匀采样出一批样本 x 0 , x 1 , x 2 . . . x n x_0, x_1, x_2... x_n x0,x1,x2...xn
- 求出 Q = ( b − a ) ∗ 1 / n ∗ ∑ i = 0 n f ( x i ) Q=(b-a)*1/n*\sum_{i=0}^n f(x_i) Q=(b−a)∗1/n∗∑i=0nf(xi)
- 求出的Q即为I的近似
*蒙特卡罗应用三：求期望
给随机变量X的概率密度函数p(x)和原函数f(x)。函数的期望定义为：
E
x
∼
p
[
f
(
x
)
]
=
∫
−
∞
∞
f
(
x
)
p
(
x
)
d
x
E_{x \sim p}[f(x)]=\int_{-\infty}^{\infty} f(x)p(x) dx
Ex∼p[f(x)]=∫−∞∞f(x)p(x)dx，那么如何求期望，有如下步骤：
- 首先，根据p(x)的分布情况进行采样，得到n个向量 X 1 , X 2 , . . . , X n X_1,X_2,...,X_n X1,X2,...,Xn
- 计算 Q n = 1 / n ∑ i = 1 n f ( X i ) Q_n = 1/n \sum_{i=1}^{n} f(X_i) Qn=1/n∑i=1nf(Xi)
- Q n Q_n Qn的值即为期望 E x ∼ p [ f ( x ) ] E_{x \sim p}[f(x)] Ex∼p[f(x)]的近似值
那么现在有个问题，给定概率密度函数p(x)之后，我们如何对p(x)进行采样，才能得到刚好符合p(x)分布的样本，上边说到全用均匀采样是不行的，而且随机变量X也有可能是高纬度的。下边展开来说几种采样的方法，最后引出吉布斯采样。
乌拉姆–随机采样
由于无法对p(x)进行均匀采样，那么我们可以对p(x)的积分F(x)，即X的累积概率分布函数进行采样，CDF的值域是[0, 1]，因此乌拉姆提出可以在[0,1]上均匀采样，之后再求F(x)的反函数，解出X的值，得到一批样本。
那么均匀分布是如何进行抽样的呢？其实我们经常用的rand()随机数就是均匀分布的。它内部的原理其实就是先生成一个[0,1]内的小随机数，然后通过
i
n
+
1
=
(
a
∗
i
n
+
c
)
(
m
o
d
M
)
i_{n+1}=(a*i_n+c)(mod \ M)
in+1=(a∗in+c)(mod M)依次生成之后的随机数。
缺点：还是要进行积分求得F(x)，但是p(x)积分未必存在，所以还是回到最初的问题，p(x)很复杂如果没法积分的话，这个随机抽样方法就无法进行。
冯·诺依曼–接受拒绝采样
为了解决上边p(x)的累积分布函数不好求的问题，冯提出一个q(x)，q(x)的累积分布是好求的，且
m
q
(
x
)
>
=
p
(
x
)
mq(x)>=p(x)
mq(x)>=p(x)，其中m是一个常数。
这样一来，可以对
m
q
(
x
)
mq(x)
mq(x)的CDF进行均匀采样，但是对其采样的结果是服从
m
q
(
x
)
mq(x)
mq(x)分布的，并不是完全服从
p
(
x
)
p(x)
p(x)分布。于是冯就提出了接受拒绝采样，对
m
q
(
x
)
mq(x)
mq(x)的CDF采样的结果是有一定的概率服从
p
(
x
)
p(x)
p(x)的，这个概率是多少呢，就是
p
(
x
)
/
m
q
(
x
)
p(x)/mq(x)
p(x)/mq(x)。因此，对i
∼
\sim
∼U[0,1]进行采样，当
i
<
(
p
(
x
i
)
/
m
q
(
x
i
)
)
i<(p(x_i)/mq(x_i))
i<(p(xi)/mq(xi))，则接受，否则就拒绝。
上边的方法貌似已经很完美了，但是仍然存在一些问题，我们采样的接受概率取决于设计的
m
q
(
x
)
mq(x)
mq(x)，当
q
(
x
)
q(x)
q(x)函数设计的好，则采样的效率很高，否则就会大部分被拒绝。
马尔科夫链-蒙特卡罗采样(MCMC采样)
什么是马尔科夫链，假设随机向量
X
=
x
0
,
x
1
,
x
2
,
.
.
.
,
x
n
X={x_0, x_1,x_2,...,x_n}
X=x0,x1,x2,...,xn，n个不完全相同的
x
x
x值组成了一个状态，那么现在有一个状态序列：
.
.
.
X
t
−
2
,
X
t
−
1
,
X
t
,
X
t
+
1
.
.
.
...X_{t-2},X_{t-1},X_{t},X_{t+1}...
...Xt−2,Xt−1,Xt,Xt+1...。马尔科夫链满足这样一个关系，后一个状态只和他前一个状态有关，即:
P
(
X
t
+
1
∣
.
.
.
,
X
t
−
2
,
X
t
−
1
,
X
t
)
=
P
(
X
t
+
1
∣
X
t
)
P(X_{t+1}|...,X_{t-2},X_{t-1},X_{t})=P(X_{t+1}|X_{t})
P(Xt+1∣...,Xt−2,Xt−1,Xt)=P(Xt+1∣Xt)，其中的P是一个状态转移矩阵，P(i,j)代表从i状态转移到j状态的概率。
马尔科夫链中，给定一个初始的概率分布和状态转移矩阵P，经过m次迭代之后都可以得到一个稳定的概率分布，什么是稳定的概率分布，即在当前时刻以及之后的时刻中，随机变量X中的所有取值的概率分布都保持不变或者微小变动。我们把X满足的分布记为
π
(
x
)
\pi(x)
π(x)。那么我们抽样的就是当马尔科夫链达到稳定状态时，之后的时刻中的X取值都可以当做我们的样本。
那么问题来了，我们如何找到一个满足要求的P（状态转移矩阵）呢？
这里数学家给出一个细致平衡条件：
π
(
i
)
P
(
i
,
j
)
=
π
(
j
)
P
(
j
,
i
)
\pi(i)P(i,j)=\pi(j)P(j,i)
π(i)P(i,j)=π(j)P(j,i)，当该条件成立时，P即为所求，即该P一定会让马尔科夫链到达一个平衡状态。那么P还是难求啊，这里我们随意引入一个
Q
(
i
,
j
)
Q(i,j)
Q(i,j),因为是随意引入的那么大概率是
π
(
i
)
Q
(
i
,
j
)
≠
π
(
j
)
Q
(
j
,
i
)
\pi(i)Q(i,j)\not=\pi(j)Q(j,i)
π(i)Q(i,j)=π(j)Q(j,i)。还是不行，我们想要让他强行成立，再引入一个
α
(
i
,
j
)
\alpha(i, j)
α(i,j)，其中
α
(
i
,
j
)
=
π
(
j
)
Q
(
j
,
i
)
\alpha(i,j)=\pi(j)Q(j,i)
α(i,j)=π(j)Q(j,i)。至此，我们终于找到满足细致平衡条件的数了，即
π
(
i
)
Q
(
i
,
j
)
α
(
i
,
j
)
=
π
(
j
)
Q
(
j
,
i
)
α
(
j
,
i
)
\pi(i)Q(i,j)\alpha(i,j)=\pi(j)Q(j,i)\alpha(j,i)
π(i)Q(i,j)α(i,j)=π(j)Q(j,i)α(j,i)。
注意看这里的
α
(
i
,
j
)
\alpha(i,j)
α(i,j),实际上他还是一个[0,1]的概率值，因此这里我们对随机矩阵Q进行采样，但是采样的结果不一定都满足要求，只有
α
(
i
,
j
)
\alpha(i,j)
α(i,j)的概率符合要求，所以这里的采样一定程度上依赖于
α
(
i
,
j
)
\alpha(i,j)
α(i,j)的值。那么如何提升
α
(
i
,
j
)
\alpha(i,j)
α(i,j)的值呢。这里一篇论文提出让
α
(
i
,
j
)
=
m
i
n
{
π
(
j
)
Q
(
j
,
i
)
π
(
i
)
Q
(
i
,
j
)
,
1
}
\alpha(i,j)=min\{\frac{\pi(j)Q(j,i)}{\pi(i)Q(i,j)}, 1\}
α(i,j)=min{π(i)Q(i,j)π(j)Q(j,i),1},论文如下图：
文章来源：https://www.toymoban.com/news/detail-720654.html
所以，整个MCMC采样的步骤如下：
文章来源地址https://www.toymoban.com/news/detail-720654.html
参考
- 【蒙特卡洛算法】 https://www.bilibili.com/video/BV1cg4y1z7rM/?share_source=copy_web&vd_source=aa275ee199b6bfcb3c4ab8e07b355199
- 【蒙特卡洛（Monte Carlo, MCMC）方法的原理和应用】 https://www.bilibili.com/video/BV17D4y1o7J2/?share_source=copy_web&vd_source=aa275ee199b6bfcb3c4ab8e07b355199
到了这里，关于概率论之蒙特卡罗模拟的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
