各种加法器的比对分析与Verilog实现（1）-Toy模板网

这篇具有很好参考价值的文章主要介绍了各种加法器的比对分析与Verilog实现（1）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

接下来几篇博客，我将介绍常见的几种加法器设计，包括超前进位、Kogge-Stone、brent-kung、carry-skip、Conditional-Sum等加法器的原理及Verilog实现。

本文将介绍行波进位加法器、超前进位加法器的原理及Verilog实现。

1. 行波进位加法器 (Ripple Carry Adder, RCA)

1.1 原理

从下方原理图即可看出，行波进位加法器由一系列全加器级联而成，这种加法器面积小，由于每一比特的进位输入必须等待前一比特完成进位输出的计算，所以这种加法器的速度慢。

1.2 Verilog实现

（1）完成单比特全加器的模块

module full_adder(
    input a,
    input b,
    input c_in,
    output sum,
    output c_out
);
		
assign {c_out,sum} = a + b + c_in;
	
endmodule

（2）全加器级联

module RCA(
    input [3:0] a,
    input [3:0] b,
    input c_in,
    output [3:0] sum,
    output c_out
);
	
wire sum1,sum2,sum3,sum4;
wire c_out1,c_out2,c_out3;
	
assign sum = {sum4,sum3,sum2,sum1};
	
full_adder f0(
    .a(a[0]),
    .b(b[0]),
    .c_in(c_in),
    .sum(sum1),
    .c_out(c_out1)
);
		
full_adder f1(
    .a(a[1]),
    .b(b[1]),
    .c_in(c_out1),
    .sum(sum2),
    .c_out(c_out2)
);
		
full_adder f2(
    .a(a[2]),
    .b(b[2]),
    .c_in(c_out2),
    .sum(sum3),
    .c_out(c_out3)
);
		
full_adder f3(
    .a(a[3]),
    .b(b[3]),
    .c_in(c_out3),
    .sum(sum4),
    .c_out(c_out)
);
	
endmodule

2. 超前进位加法器 (Carry Look Ahead Adder , CLA)

2.1 设计原理

我们可以按A、B异或结果和A·B结果分成3组（表中用不同颜色进行区分），不难发现，第一组没有进位，第三组必有进位，第二组中Ci为1则有进位。因此可以通过这种特性提前得到进位。

定义：

行波进位加法器,FPGA求学之路,fpga开发

根据真值表的特点可以推出：

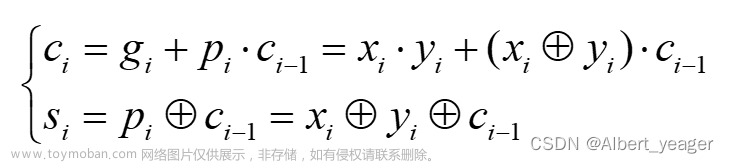
行波进位加法器,FPGA求学之路,fpga开发

因此，CLA的计算流程如下：

1) 对面向输入的第一层，并行预计算gi和pi

2) 计算进位ci

3) 根据pi和ci计算si

超前进位加法器优化改进行波进位器的关键路径，通过采用并行计算进位的方法，解决了行波进位加法器的进位依赖问题。然而对于大位宽的超前进位加法器，进位逻辑计算单元面积耗费大。

2.2 Verilog实现

（1）pg单元设计

module pg_cell(
    input a,
    input b,
    output g,
    output p
);

assign g = a & b;
assign p = a ^ b;

endmodule

（2）CLA实现

module LCA #(width=4) (
    input  [width-1:0] op1,
    input  [width-1:0] op2,
    input  cin,
    output [width-1:0] sum1,
    output [width-1:0] sum2,
    output cout,
    output cout2
);
//CLA
wire [width-1:0] g;
wire [width-1:0] p;
wire [width:0] c;
//gp generator
genvar i;
for( i=0; i<width; i=i+1) begin
pg_cell pg_cell_u(
    .a( op1[i]),
    .b( op2[i]),
    .g( g[i]  ),
    .p( p[i]  )
);
end
//carry generator
assign c[0] = cin;
assign c[1] = g[0] + ( c[0] & p[0] );
assign c[2] = g[1] + ( (g[0] + ( c[0] & p[0]) ) & p[1] );
assign c[3] = g[2] + ( (g[1] + ( (g[0] + (c[0] & p[0]) ) & p[1])) & p[2] );
assign c[4] = g[3] + ( (g[2] + ( (g[1] + ( (g[0] + (c[0] & p[0]) ) & p[1])) & p[2] )) & p[3]);
assign cout = c[width];

genvar k;
for( k=0; k<width; k=k+1) begin
    assign sum1[k] = p[k] ^ c[k];
end

endmodule