基于Dijkstra算法的机器人编队路径规划问题-Toy模板网

这篇具有很好参考价值的文章主要介绍了基于Dijkstra算法的机器人编队路径规划问题。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

基于Dijkstra算法的机器人编队路径规划问题

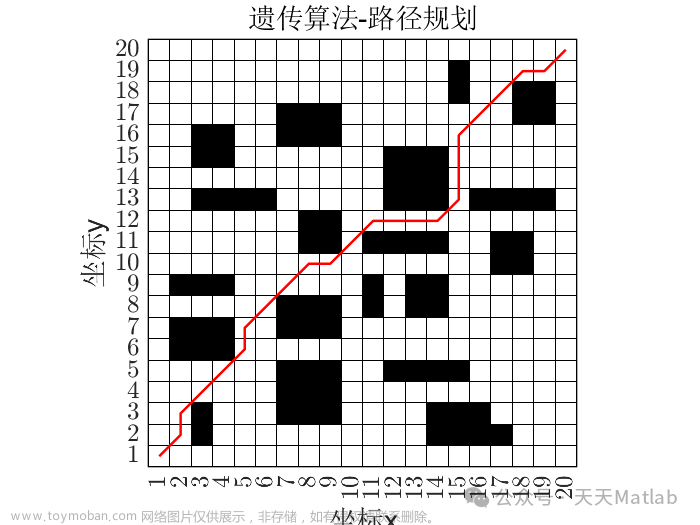
路径规划是机器人领域中的一个重要问题，它涉及确定从起点到目标点的最佳路径。Dijkstra算法是一种经典的图算法，用于解决最短路径问题。在本文中，我们将介绍如何使用Dijkstra算法来实现机器人编队的路径规划，并提供相应的MATLAB代码。

问题描述：
假设我们有一个机器人编队，由多个机器人组成。每个机器人都位于一个离散化的二维空间中，并且可以沿上、下、左、右四个方向移动。编队中的每个机器人都具有一个起点和一个目标点，我们的目标是找到每个机器人从其起点到目标点的最短路径，以便整个编队能够以最短的总路径到达目标。

解决方案：
我们可以使用Dijkstra算法来解决这个问题。Dijkstra算法是一种基于图的贪心算法，它从起点开始，逐步扩展到其他节点，并找到从起点到每个节点的最短路径。

首先，我们需要将问题转化为图的形式。我们可以将每个机器人的位置看作图中的一个节点，节点之间的连接表示机器人之间的移动关系。然后，我们需要为每个连接分配一个权重，表示从一个节点到另一个节点的移动代价。在这个问题中，我们可以将每个连接的权重设置为1，因为机器人只能沿上、下、左、右四个方向移动，且每个移动步骤的代价相同。

接下来，我们可以使用Dijkstra算法来找到从起点到每个节点的最短路径。算法的基本思想是维护一个距离数组，用于记录从起点到每个节点的当前最短路径的长度。初始时，起点的距离为0，其他节点的距离为无穷大。然后，我们从起点开始，逐步扩展到其他节点，每次选择距离最小的节点，并更新与其相邻节点的距离。重复这个过程，直到所有节点都被访问。

下面是MATLAB代码实现：文章来源地址https://www.toymoban.com/news/detail-721105.html

到了这里，关于基于Dijkstra算法的机器人编队路径规划问题的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！