【2023Mathorcup大数据】B题 电商零售商家需求预测及库存优化问题 python代码解析
1 题目
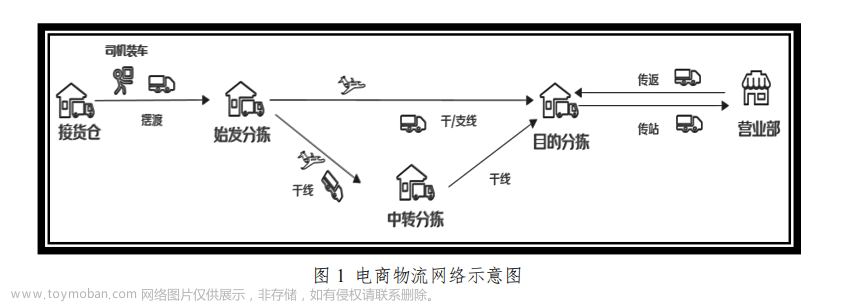
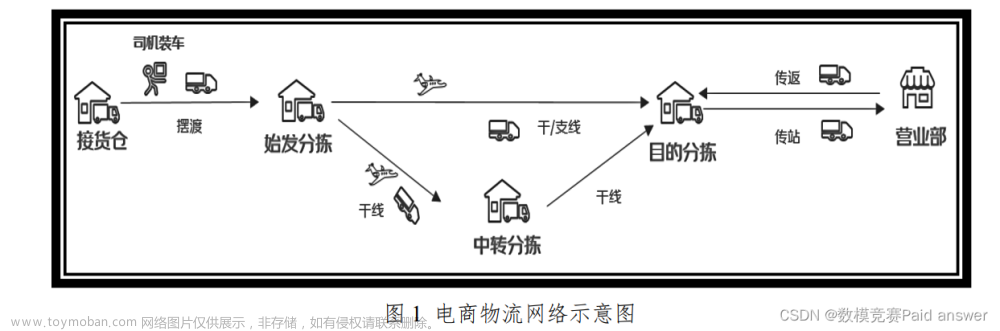
2023 年MathorCup 高校数学建模挑战赛——大数据竞赛赛道B:电商零售商家需求预测及库存优化问题电商平台存在着上千个商家,他们会将商品货物放在电商配套的仓库,电商平台会对这些货物进行统一管理。通过科学的管理手段和智能决策,大数据智能驱动的供应链可以显著降低库存成本,同时保证商品的按时履约。一般来说,以上供应链优化问题会包含以下方面:
(1)需求预测
预测往往是智能供应链的决策基础,它可以让管理者提前预知各地的需求,从而将库存提前放在靠近需求的仓库中,此时的预测任务为:根据历史一段时间的需求量,预测各仓库中各商品未来需求,“预测维度”即为不同商家在各仓库中存放的各种商品每天的数量。一般来说,企业会首先根据数据的历史情况,分析出需求量序列的数理特征,对相似的需求量序列进行归类,并根据分类结果做到更加精准的预测。预测准确率有很多评价指标,较常用的指标为 1-wmape,定义如下:
1
−
w
m
a
p
e
=
1
−
∑
∣
y
i
−
y
i
^
∣
∑
y
i
1-wmape = 1-\frac{\sum {|y_i-\hat{y_i}|}}{\sum{y_i}}
1−wmape=1−∑yi∑∣yi−yi^∣
其中 y i y_i yi为第个序列(商家在各仓库中存放的各种商品每天的数量)的真实需求量, y i ^ \hat{y_i} yi^为第个序列的预测需求量。
然而,在实际的电商供应链预测任务中,常常会出现多种不同的问题。例如,部分商品的销售时间过短、仓库存在新增或切换等情况,导致该预测维度下历史数据过少;另外,部分大型促销期间货量的陡增并由此带来的不规律性,也给需求量的精准预测带来了不小的难度。此时便需要通过算法得到历史一般规律,找出相似的历史情况(如相似的仓或商品),从而实现精准预测。
(2)库存优化
为了有效管理库存水平,企业通常会制定各种库存策略来控制商品的补货频次和补货量。定期盘点库存策略(s,S)是一种常见的库存策略,其中
s 表示该种策略下的库存下限,S 为库存上限。在这种策略中,企业会每隔一段固定时间查看库存水平,盘点之间的间隔设为盘点周期(NRT)。如果在盘点时库存水平T 低于最小库存水平s,则会将库存补充至S,此时的补货量 Q = S − T,如果在盘点时库存水平高于 s,则不进行补充,直到下一次库存盘点。同时需要考虑到,在每次发起补货后,补充的货物会经过一定时间后才能到达当前仓库,这个时间间隔为提前期(LT)。
使用以上的库存策略,管理者需要对两个方面进行权衡取舍。一方面,为了及时满足用户订单,公司需要保有大量库存以防止缺货;另一方面,库存水位升高带来了过高的库存成本。库存优化的目标主要为:
1) 降低库存总持有成本,可由单位持有成本h 得到(一件商品存储一天产生的成本);
2) 满足服务水平:确保有足够的产品可以及时满足客户需求,降低总缺货成本,可由缺货成本得到(每天每缺一件商品产生的成本);
3) 降低库存周转天数:库存周转天数越小,表示库存的流动性越好,企业的库存管理效率越高。
服务水平及库存周转天数计算公式为:
$$
服务水平=\frac{被满足的商品件数}{实际需求总件数} × 100 % \
库存周转天数 =\frac{期初库存书刘昂+期末库存数量}{2}× \frac{计算时间段内天数}{计算时间段内总销量}
$$
现有一张电商零售商家的历史出货量表(附件 1),给出了历史 6 个月各商家存放在电商不同仓库的商品每天的出货量。假设该出货量即为历史各商品在各仓库的需求量。同时,还可以取到各商品、商家、仓库的信息(附件 2-4),例如分类、品牌、生效日期等,这些信息的选择和引入会帮助更好的预测并管理供应链中的库存。
1.1 初赛问题
问题一: 使用附件 1-4 中的数据, 预测出各商家在各仓库的商品2023-05-16 至 2023-05-30 的需求量,请将预测结果填写在结果表 1 并上传至竞赛平台,并对你们模型的预测性能进行评价。另外请讨论:根据数据分析及建模过程,这些由商家、仓库、商品形成的时间序列如何分类,使同一类别在需求上的特征最为相似?
**问题二:**现有一些新出现的商家+仓库+商品维度(附件 5),导致这种情况出现的原因可能是新上市的商品,或是改变了某些商品所存放的仓库。请讨论这些新出现的预测维度如何通过历史附件 1 中的数据进行参考,找到相似序列并完成这些维度在 2023-05-16 至 2023-05-30 的预测值。请把预测结果填写在结果表 2,并上传至竞赛平台。
**问题三:**每年 6 月会出现规律性的大型促销,为需求量的精准预测以及履约带来了很大的挑战。附件 6 给出了附件 1 对应的商家+仓库+商品维度在去年双十一期间的需求量数据,请参考这些数据,给出 2023-06-01 至2023-06-20 的预测值。请把预测结果填写在结果表 3,并上传至竞赛平台。
注:结果表 1-3 打包一个压缩包,“结果表.zip”,提交 zip 文件到竞赛系统中。
附件1-4的字段说明:
附件 1:商家历史出货量表
| 字段名 | 字段类型 | 描述 |
|---|---|---|
| seller_no | String | 商家编码 |
| product_no | String | 商品编码 |
| warehouse_no | String | 仓库编码 |
| date | String | 日期 |
| qty | Float | 出货量(可看做需求量) |
附件 2:商品信息表
| 字段名 | 字段类型 | 描述 |
|---|---|---|
| product_no | String | 商品编码 |
| category1 | String | 商品一级分类 |
| category2 | String | 商品二级分类 |
| category3 | String | 商品三级分类 |
附件 3:商家信息表
| 字段名 | 字段类型 | 描述 |
|---|---|---|
| seller_no | String | 商家编码 |
| seller_category | String | 商家分类 |
| inventory_category | String | 库存分类 |
| seller_level | String | 商家规模 |
附件 4:仓库信息表
| 字段名 | 字段类型 | 描述 |
|---|---|---|
| warehouse_no | String | 仓库编码 |
| warehouse_category | String | 仓库类别 |
| warehouse_region | String | 仓库区域 |
2 问题分析
2.1 问题一
(1)数据预处理:读取附件1-4的数据文件,进行数据清洗和转换,可考虑进行以下操作:
- 将“日期”字段转换为datetime格式,并提取出年、月、日等信息;
- 将附件2、3、4中的分类信息进行Label Encoding,将分类信息转换为数字标签;
- 可以通过统计分析、可视化等手段对数据进行初步探索和分析,例如:
- 商家、仓库、商品的数量分布情况;
- 商家、仓库、商品之间的相关性分析等。
(2)特征工程:对表格进行透视或分组操作,生成对应时间序列的统计特征,例如:
- 统计每个商家在每个仓库中每天/周/月的平均销量、总销量、销售额等信息;
- 构建时间窗口特征,例如每个商家在每个仓库中最近1周、1个月、3个月、6个月等时间段内的销售量、均值以及波动情况等。
(3)时间序列预测:针对每个商家、仓库、商品的时间序列统计特征,使用ARIMA、Prophet、LSTM等时间序列预测模型进行预测,并得出下一个时间段内的需求量预测值。代码实现以ARIMA为例。
(4)结果输出:按照表5的格式输出预测结果
(5)分类方法:可以考虑聚类算法,将同一类别的商家、仓库、商品按照需求量相似性进行分组,然后对每一个簇进一步分析,例如:
- K-means算法:基于样本的相似性对样本进行分群;
- 层次聚类算法:将潜在的类别从候选集合中逐层聚合。
(6)相似性评测:通过度量分类以上聚类结果的质量,计算同一类别内的商家、仓库、商品之间的相似程度,以便为商家提供更加精准的预测及建议。常用的质量评价标准有轮廓系数、Calinski-Harabasz指数、Davies-Bouldin指数等。
(7)反馈优化:根据预测结果和分类分析的结果,进一步分析结论,给商家几个建议和优化方案。
2.2 问题二
(1)对附件1中所有商家、仓库、商品组合,按时间顺序生成其历史出货量时间序列,对于新增的商家+仓库+商品维度在附件5中可以视为只有一条历史记录。
(2)对于新增的商家+仓库+商品维度,在附件1中搜索与其最为相似的历史时间序列,可以使用聚类分析或其他相似度度量方法进行相似性计算。代码中采用欧式距离的方式。使用cdist()函数计算子集(seller_no和warehouse_no相同)的qty列和附件5的qty列之间计算欧氏距离。最后使用np.argmin()函数找到距离数组distances中具有最小值的索引值。这表示找到了在附件5中最相似的历史序列。
(3)将找到的最为相似的历史时间序列作为该新增维度的需求量时间序列,使用与问题一相同的方法进行预测并填写结果表2。
2.3 问题三
(1)使用附件1中给出的商家+仓库+商品的历史需求量数据,加上附件6中相应的需求量数据,按照时间顺序生成历史需求量时间序列。
(2)对历史时间序列进行特征工程,提取时间维度,周几、月份、节假日等特征,并进行预处理操作(如平滑、滑动平均等)。
(3)使用时间序列预测模型进行训练,并对2023-06-01 至2023-06-20 的需求量进行预测。
3 代码实现
3.1 问题一
import pandas as pd
import numpy as np
from datetime import datetime
from sklearn.preprocessing import LabelEncoder
import matplotlib.pyplot as plt
import warnings
warnings.filterwarnings('ignore')
plt.rcParams['font.sans-serif'] = ['STSong']
(1)数据预处理
对类别特征编码
# 数据预处理
# 读取商家历史出货量表
df_sales = pd.read_excel('附件表/附件1-商家历史出货量表.xlsx')
# 将日期字段转换为datetime格式
df_sales['date'] = pd.to_datetime(df_sales['date'])
df_sales['year'] = df_sales['date'].dt.year
df_sales['month'] = df_sales['date'].dt.month
df_sales['day'] = df_sales['date'].dt.day
# 读取商品信息表
df_product = pd.read_excel('附件表/附件2-商品信息表.xlsx')
# 使用Label Encoder对商品分类信息进行编码
le = LabelEncoder()
df_product['category1'] = le.fit_transform(df_product['category1'])
df_product['category2'] = le.fit_transform(df_product['category2'])
df_product['category3'] = le.fit_transform(df_product['category3'])
# 读取商家信息表
df_seller = pd.read_excel('附件表/附件3-商家信息表.xlsx')
# 使用Label Encoder对商家分类信息进行编码
df_seller['seller_category'] = le.fit_transform(df_seller['seller_category'])
df_seller['inventory_category'] = le.fit_transform(df_seller['inventory_category'])
df_seller['seller_level'] = le.fit_transform(df_seller['seller_level'])
# 读取仓库信息表
df_warehouse = pd.read_excel('附件表/附件4-仓库信息表.xlsx')
# 使用Label Encoder对仓库分类信息进行编码
df_warehouse['warehouse_category'] = le.fit_transform(df_warehouse['warehouse_category'])
df_warehouse['warehouse_region'] = le.fit_transform(df_warehouse['warehouse_region'])
(2)统计商家、仓库、商品的数量分布情况
# 统计商家、仓库、商品的数量分布情况
seller_count = df_sales['seller_no'].nunique()
warehouse_count = df_sales['warehouse_no'].nunique()
product_count = df_sales['product_no'].nunique()
print("商家数量:", seller_count)
print("仓库数量:", warehouse_count)
print("商品数量:", product_count)
# 商家、仓库、商品之间的相关性分析
sales_groupby_seller = df_sales.groupby('seller_no')['qty'].sum().reset_index()
sales_groupby_warehouse = df_sales.groupby('warehouse_no')['qty'].sum().reset_index()
sales_groupby_product = df_sales.groupby('product_no')['qty'].sum().reset_index()
plt.figure(figsize=(10, 4))
plt.subplot(131)
plt.bar(sales_groupby_seller['seller_no'], sales_groupby_seller['qty'])
plt.xlabel('商家编码')
plt.ylabel('销售量')
plt.title('商家销售量分布')
plt.subplot(132)
plt.bar(sales_groupby_warehouse['warehouse_no'], sales_groupby_warehouse['qty'])
plt.xlabel('仓库编码')
plt.ylabel('销售量')
plt.title('仓库销售量分布')
plt.subplot(133)
plt.bar(sales_groupby_product['product_no'], sales_groupby_product['qty'])
plt.xlabel('商品编码')
plt.ylabel('销售量')
plt.title('商品销售量分布')
plt.tight_layout()
plt.savefig('img/1.png',dpi=200)
plt.show()
商家数量: 35
仓库数量: 54
商品数量: 1212

(2)特征工程
# 统计每个商家在每个仓库每个商品中每天的平均销量、总销量等信息
sales_agg = df_sales.groupby(['seller_no','product_no', 'warehouse_no', 'date']).agg({
'qty': ['mean', 'sum']
}).reset_index()
sales_agg.columns = ['seller_no','product_no','warehouse_no', 'date', 'avg_qty', 'total_qty']
# # 构建时间窗口特征
sales_agg['rolling_mean_7d'] = sales_agg.groupby(['seller_no','product_no','warehouse_no'])['total_qty'].rolling(7).mean().reset_index(2, drop=True).reset_index()['total_qty']
sales_agg['rolling_mean_30d'] = sales_agg.groupby(['seller_no','product_no', 'warehouse_no'])['total_qty'].rolling(30).mean().reset_index(2, drop=True).reset_index()['total_qty']
sales_agg['rolling_std_30d'] = sales_agg.groupby(['seller_no','product_no', 'warehouse_no'])['total_qty'].rolling(7).std().reset_index(2, drop=True).reset_index()['total_qty']
sales_agg

(3)时间序列预测
店铺、商品、仓库对应的每一个时间序列,都要建立一个模型
from statsmodels.tsa.arima.model import ARIMA
df = sales_agg
# 选取一个seller、产品、仓库,每个都要计算一遍
seller_list = sales_agg['seller_no'].unique()
warehouse_list = sales_agg['warehouse_no'].unique()
product_list = sales_agg['product_no'].unique()
result_table1 = []
df1_grouped = sales_agg.groupby(['seller_no','product_no','warehouse_no'])
for (seller_no,product_no,warehouse_no), df1_group in df1_grouped:
# # 训练模型
model = ARIMA(ts_data, order=(1, 1, 1)).fit()
# # 预测
predict = model.predict(start=len(ts_data)+1, end=len(ts_data)+15, dynamic=True)
# # 将预测值转化成DataFrame并返回
result = pd.DataFrame(columns=['seller_no','product_no','warehouse_no','date','forecast_qty'])
result['seller_no'] = [seller_no]*15
result['product_no'] = [product_no]*15
result['warehouse_no'] = [warehouse_no]*15
result['date']= pd.date_range(start='2023-05-16', periods=15, freq='D')
result['forecast_qty'] = list(predict)
result_table1.append(result)
merged_df = pd.concat(result_table1, axis=0, ignore_index=True)
merged_df.to_excel('结果表/结果表1-预测结果表.xlsx',index=False)
(4)聚类分析
import pandas as pd
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import LabelEncoder
# 读取商家历史出货量表
df_sales = pd.read_excel('附件表/附件1-商家历史出货量表.xlsx')
# 读取商品信息表
df_product = pd.read_excel('附件表/附件2-商品信息表.xlsx')
# 读取商家信息表
df_seller = pd.read_excel('附件表/附件3-商家信息表.xlsx')
# 读取仓库信息表
df_warehouse = pd.read_excel('附件表/附件4-仓库信息表.xlsx')
# 将日期转换为时间序列
df_sales['date'] = pd.to_datetime(df_sales['date'])
# 合并商家历史出货量表和商品信息表
df_merge = df_sales.merge(df_product, on='product_no')
# 合并商家历史出货量表、商品信息表和商家信息表
df_merge = df_merge.merge(df_seller, on='seller_no')
# 合并商家历史出货量表、商品信息表、商家信息表和仓库信息表
df_merge = df_merge.merge(df_warehouse, on='warehouse_no')
# 选择需要的特征列
df_feature = df_merge[['seller_no', 'product_no', 'warehouse_no', 'category1', 'category2', 'category3', 'seller_category','inventory_category', 'seller_level', 'warehouse_category', 'warehouse_region', 'qty']]
# 对分类特征进行编码
# 创建LabelEncoder对象
label_encoder = LabelEncoder()
# 需要进行数值编码的列名
cat_cols = ['category1', 'category2', 'category3', 'seller_category','inventory_category', 'seller_level', 'warehouse_category', 'warehouse_region']
# 循环对每个类别特征进行数值编码
for col in cat_cols:
df_feature[col] = label_encoder.fit_transform(df_feature[col])
df_feature

# 对数值特征进行归一化
from sklearn.preprocessing import MinMaxScaler
# 创建MinMaxScaler对象
scaler = MinMaxScaler()
df_feature_2 = df_feature.drop(columns=['seller_no','product_no','warehouse_no'])
# 对df_feature进行归一化
df_feature_normalized = pd.DataFrame(scaler.fit_transform(df_feature_2), columns=df_feature_2.columns)
df_feature_normalized

选择最佳的聚类K值和随机种子
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
# 创建一个空列表存储不同K值下的SSE得分
sse_scores = []
# 定义待测试的K值范围
k_values = range(2, 10)
# 定义最佳的K值和随机种子变量
best_k = 0
best_random_state = 0
best_sse = float('inf') # 初始值设为正无穷大
# 循环测试不同的K值和随机种子
for k in k_values:
for random_state in range(10):
# 初始化KMeans模型
kmeans = KMeans(n_clusters=k, random_state=random_state)
# 训练模型
kmeans.fit(df_feature_normalized)
# 计算SSE得分并存储到列表中
sse = kmeans.inertia_
sse_scores.append((k, random_state, sse))
# 比较得分,更新最佳的K值和随机种子
if sse < best_sse:
best_k = k
best_random_state = random_state
best_sse = sse
# 打印最佳的K值和随机种子
print("最佳的K值:", best_k)
print("最佳的随机种子:", best_random_state)
最佳的K值: 3
最佳的随机种子: 7
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
best_k = 3
best_random_state = 7
# 可视化最佳K值和随机种子下的聚类结果
kmeans_best = KMeans(n_clusters=best_k, random_state=best_random_state)
kmeans_best.fit(df_feature_normalized)
labels = kmeans_best.labels_
# 使用PCA将数据降至3维
pca = PCA(n_components=3)
df_feature_3d = pca.fit_transform(df_feature_normalized)
# 可视化最佳K值和随机种子下的聚类结果
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(df_feature_3d[:, 0], df_feature_3d[:, 1], df_feature_3d[:, 2], c=labels, cmap='viridis')
ax.set_title('Clustering Result (K={}, Random State={})'.format(best_k, best_random_state))
plt.savefig('img/2.png',dpi=300)
plt.show()

根据以上的聚类效果,建议再进一步数据分析每个簇的数据,具有哪些共同特征,然后反馈得到结论。
3.2 问题二
遍历附件5的序列数据,在附件1中查找相似的序列数据,这里采用的欧式距离,建议其他相似度计算方式。
实现原理是,通过groupby方法,将附件5和附件1 的数据分组,得到时间序列数据,只要在附件1中找到最相似的时间序列,就用此序列来训练模型,以此来预测未来的数据,作为附件5的预测结果。因为附件5中只有33个样本,是不足以拿来直接训练模型的,而附件1中又166个样本,训练的模型更可靠。算是一种模糊预测。
注意在计算欧式距离时,需要两个序列长度是一样的,那就取附件1中的倒数的数据和附件5中的数据对齐,意思是都是选择最新的数据对其来计算相似度。
import pandas as pd
import numpy as np
from scipy.spatial.distance import cdist
from statsmodels.tsa.arima.model import ARIMA
from scipy.spatial.distance import euclidean
import warnings
warnings.filterwarnings('ignore')
# 读取附件1和附件5的数据
df1 = pd.read_excel('附件表/附件1-商家历史出货量表.xlsx')
df5 = pd.read_excel('附件表/附件5-新品历史出货量表.xlsx')
# 整理成合适的数据格式,使用Pandas的DataFrame
df1['date'] = pd.to_datetime(df1['date'])
df1 = df1.sort_values('date')
df5['date'] = pd.to_datetime(df5['date'])
df5 = df5.sort_values('date')
# 根据附件5中的新维度,在附件1的数据中找到相似的历史序列
# 对df1按照seller_no、warehouse_no、product_no分组,得到每个组内的数据。
# 类似pivot table,但是pivot table之后需要reset_index,但是groupby不用,因此groupby更方便
df1_grouped = df1.groupby(['seller_no', 'warehouse_no', 'product_no'])
# 对df5按照seller_no、warehouse_no、product_no进行groupby
df5_grouped = df5.groupby(['seller_no', 'warehouse_no', 'product_no'])
# 计算每一个df5的序列与df1的每一个序列的距离,选择最小距离的序列作为匹配的序列
result = []
i = 0
for (seller_no, warehouse_no, product_no), df5_group in df5_grouped:
min_distance = float('inf') # 初始化最小距离为无穷大
matched_sequence = None # 初始化匹配的序列为None
for (s1, w1, p1), df1_group in df1_grouped:
seq1 = list(df5_group['qty'])
seq2 = list(df1_group['qty'])
# 向前补充0使得seq1和seq2的长度相同
if len(seq1) < len(seq2):
seq2 = seq2[-len(seq1):]
elif len(seq1) > len(seq2):
seq1 = seq1[-len(seq2):]
distance = euclidean(seq1,seq2)# 计算距离
if distance < min_distance:
min_distance = distance
matched_sequence = (s1, w1, p1,seller_no, warehouse_no, product_no)
result.append(matched_sequence)
# 将结果输出到DataFrame中
result_df = pd.DataFrame(result, columns=['seller_no_df1', 'warehouse_no_df1', 'product_no_df1', 'seller_no_df5', 'warehouse_no_df5', 'product_no_df5'])
result_df.to_excel('结果表/问题2-相似序列表.xlsx',index=False)
print(result_df.head())

根据相似的序列来建模并预测,作为附件5的预测结果
# 进行预测
from statsmodels.tsa.arima.model import ARIMA
df1 = pd.read_excel('附件表/附件1-商家历史出货量表.xlsx')
df5 = pd.read_excel('附件表/附件5-新品历史出货量表.xlsx')
result_df = result_df.drop_duplicates(subset=['seller_no_df5', 'warehouse_no_df5', 'product_no_df5'])
result_table2 = []
for index, row in result_df.iterrows():
seller_no, warehouse_no,product_no, seller_no_df5, product_no_df5, warehouse_no_df5 = row
# 类别销售数据按照日期排序
ts_data = df1[(df1['seller_no'] == seller_no)& (df1['product_no'] == product_no) & (df1['warehouse_no'] == warehouse_no)][['date', 'qty']]
if len(ts_data)>0:
ts_data = ts_data.sort_values('date')
ts_data = ts_data.set_index('date')
# # 训练模型
model = ARIMA(ts_data, order=(1, 1, 1)).fit()
# # 预测
predict = model.predict(start=len(ts_data)+1, end=len(ts_data)+15, dynamic=True)
# # # 将预测值转化成DataFrame并返回
result = pd.DataFrame(columns=['seller_no','product_no','warehouse_no','date','forecast_qty'])
result['seller_no'] = [seller_no_df5]*15
result['product_no'] = [product_no_df5]*15
result['warehouse_no'] = [warehouse_no_df5]*15
result['date']= pd.date_range(start='2023-05-16', periods=15, freq='D')
result['forecast_qty'] = list(predict)
result_table2.append(result)
保存为提交结果
pd.concat(result_table2, axis=0, ignore_index=True).to_excel('结果表/结果表2-预测结果表.xlsx', index=False)

3.3 问题三
请下载完整代码文章来源:https://www.toymoban.com/news/detail-721223.html
4 下载方式
 文章来源地址https://www.toymoban.com/news/detail-721223.html
文章来源地址https://www.toymoban.com/news/detail-721223.html
到了这里,关于【2023Mathorcup大数据】B题 电商零售商家需求预测及库存优化问题 python代码解析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!