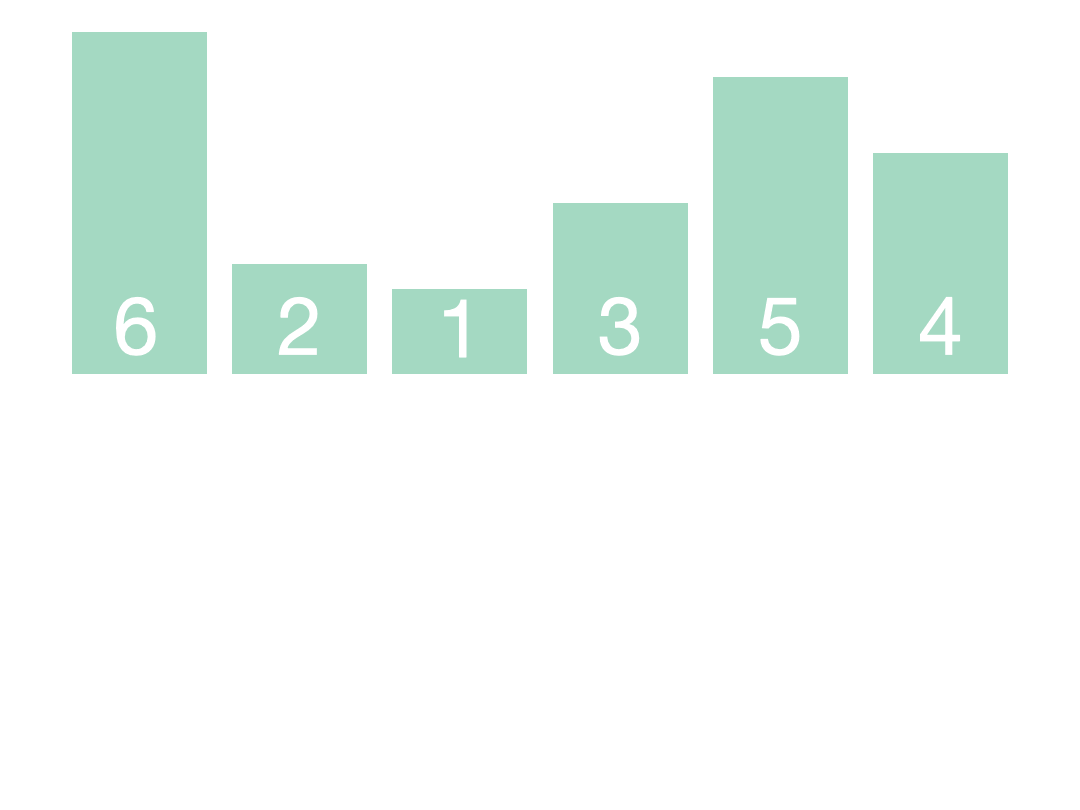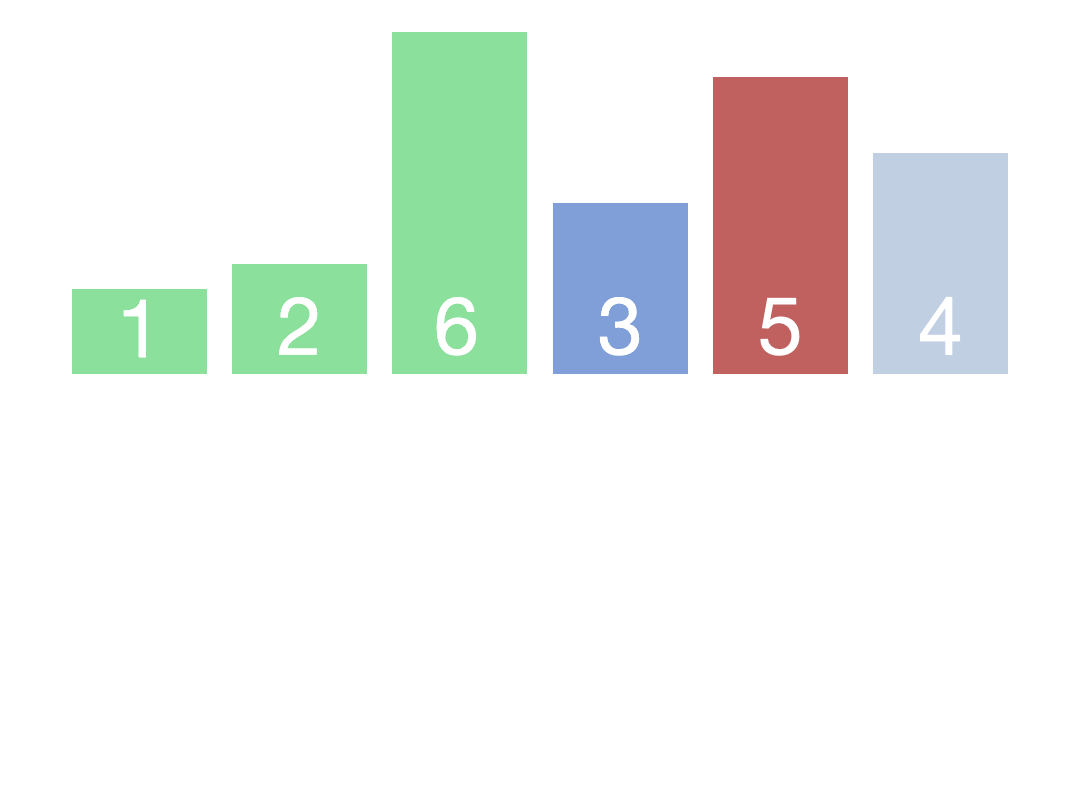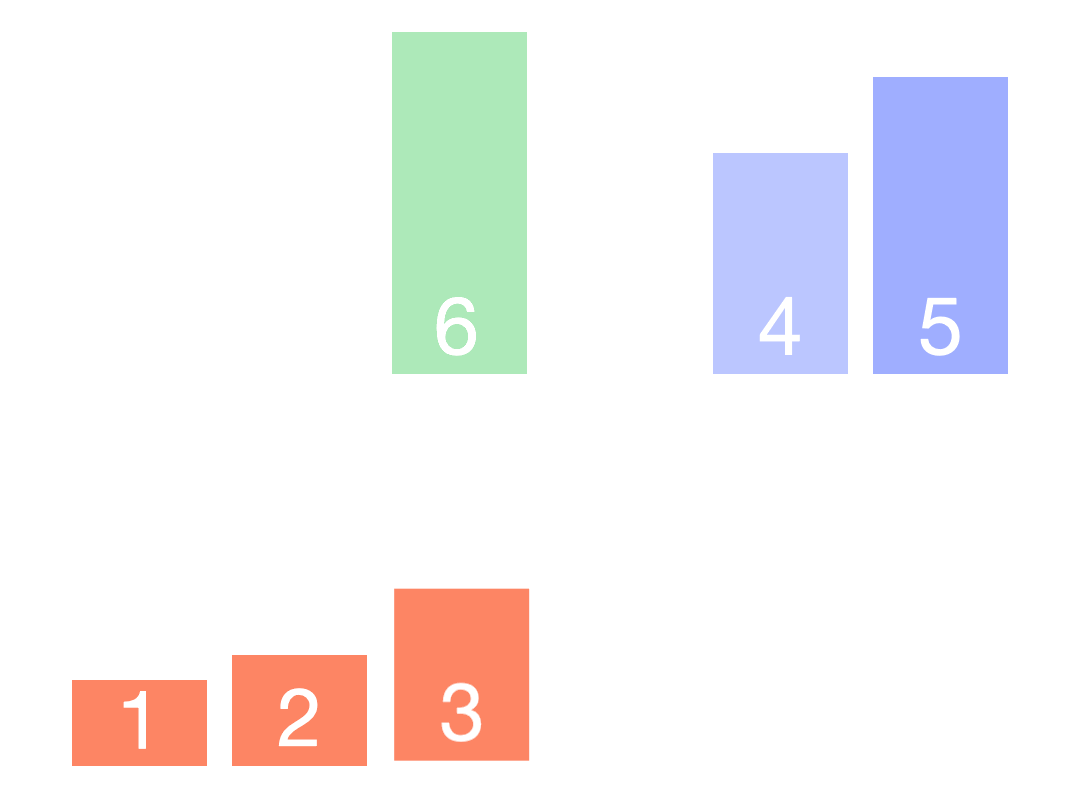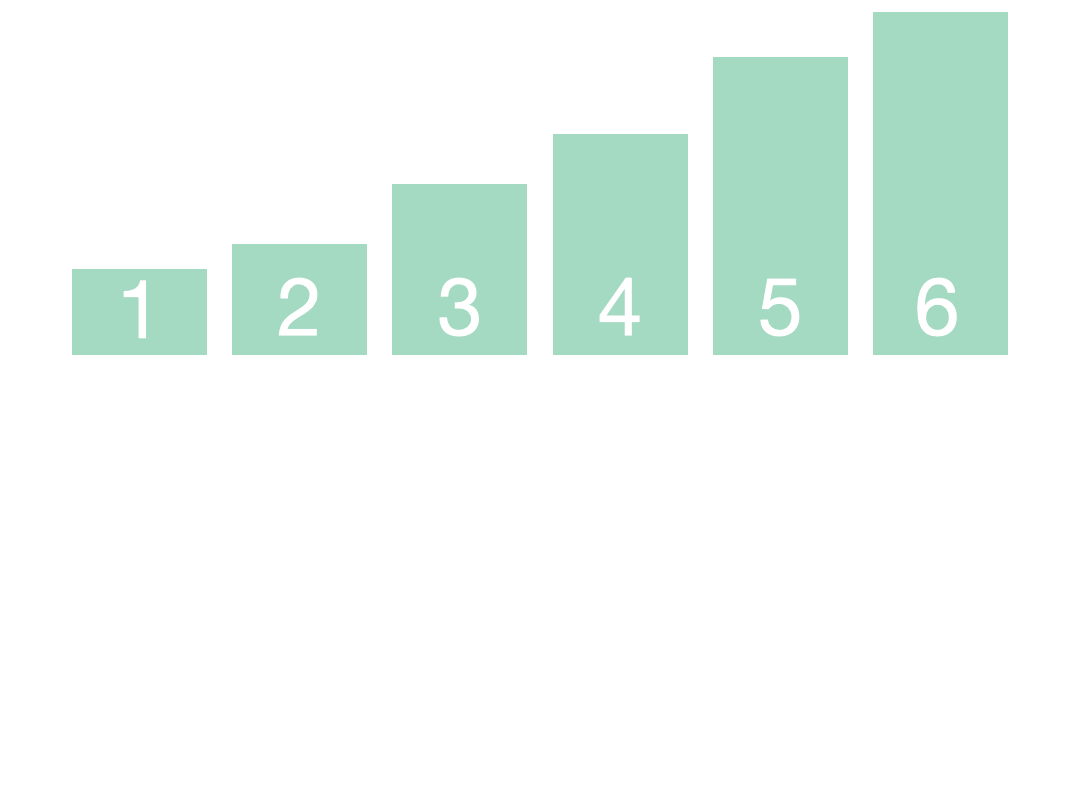情景引入
一个无环的有向图称作有向无环图(Directed Acycline Graph),简称DAG图。
DAG图是描述含有公共子式的表达式的有效工具。
在一个表示工程的有向图中,用顶点表示活动,用弧表示活动之间的优先关系,称这种有向图为顶
点表示活动的网,简称AOV网。
AOV网中不能出现回路,而判断一个AOV网是否有回路,可以通过“拓扑排序”来判断。
算法思想
1.从一个AOV网中选择一个没有前驱的顶点输出它。
2.从AOV网中删除该顶点,并且删去所有以该顶点为尾的弧。
3.重复上述两步,直到顶点全部被输出,或AOV网中不存在没有前驱的顶点位置。
显然,若最后顶点全部被输出,代表AOV网中没有回路。
若顶点没有被全部输出,即AOV网中还存在有前驱的顶点。
那么,在程序层次我们该怎么实现呢?
因为在拓扑排序中需要查找所有以某个顶点为尾的弧,需要找到该顶点的所有出边,为此,图应该
采用邻接表存储。
同时,因为还要判断某个顶点有没有入度,即找到没有前驱的顶点,我们还需要一个辅助数组
degree数组用来确定某个顶点的入度。
另外,为了防止重复检测入度为0的顶点,可以设置一个栈来暂存所有入度为0的顶点。
代码部分
#include<stdio.h>
#include<malloc.h>
#define MAX 100
typedef struct ArcNode{
int adjvex;
int weight;
struct ArcNode *nextarc;
}ArcNode;
typedef struct VNode{
char vertex;
ArcNode *firstarc;
}VNode;
typedef VNode AdjList[MAX];
typedef struct ALGraph{
AdjList adjlist;
int vexnum,arcnum;
}ALGraph;
int LocateVertex(ALGraph *G,char v)
{
int k;
for(k=0;k<G->vexnum;k++)
if(G->adjlist[k].vertex == v)
return k;
return -1;
}
void CreateALGraph(ALGraph *G)
{
int i,l1,l2,weight;
char v1,v2;
printf("请输入顶点数和边数:\n");
scanf("%d%d",&G->vexnum,&G->arcnum);
getchar();
printf("请输入{%d}个顶点:\n",G->vexnum);
for(i=0;i<G->vexnum;i++){
scanf("%c",&G->adjlist[i].vertex);
G->adjlist[i].firstarc = NULL;
}
getchar();
printf("请输入{%d}条边,格式如(v1 v2 权值)\n",G->arcnum);
for(i=0;i<G->arcnum;i++){
scanf("%c %c %d",&v1,&v2,&weight);
getchar();
l1 = LocateVertex(G,v1);
l2 = LocateVertex(G,v2);
if(l1 == -1 || l2 == -1){
printf("失败.\n");
i = i - 1;
continue;
}
else{
ArcNode *tmp = (ArcNode*)malloc(sizeof(ArcNode));
tmp->adjvex = l2;
tmp->weight = weight;
tmp->nextarc = G->adjlist[l1].firstarc;
G->adjlist[l1].firstarc = tmp;
printf("成功.\n");
}
}
}
void FindInDegree(ALGraph *G,int *indegree) //求入度函数
{
int i;
ArcNode *p;
for(i=0;i<G->vexnum;i++)
indegree[i] = 0; //初始化 indegree数组全部置为0
for(i=0;i<G->vexnum;i++){
p = G->adjlist[i].firstarc;
while(p){ //对p节点进行遍历
indegree[p->adjvex]++; //对应索引入度加一
p = p->nextarc;
}
}
}
void TopologicalSort(ALGraph *G,int n)
{
int indegree[n];
int i,j,count;
int top;
ArcNode *p;
FindInDegree(G,indegree); //求该图的所有顶点入度
top = 0;
for(i=0;i<G->vexnum;i++){ //遍历图中顶点入度为0的顶点
if(indegree[i] == 0){ //如果顶点入度为0,那么入栈
indegree[i] = top; //令该顶点值为top指针的值
top = i + 1; //top指针加一
}
}
count = 0;
while(top!=0){
i = top - 1; //top指针减一
top = indegree[i];
printf("移除顶点:{%c}\n",G->adjlist[i].vertex);
count++;
for(p=G->adjlist[i].firstarc;p;p=p->nextarc){ //模拟移除以该顶点为弧尾的边
j = p->adjvex; //这里的移除边,并不是真的删除这条边,而是数量减一
if(--indegree[j] == 0){ //--表示该顶点入度减一后是否为0
indegree[j] = top; //如果入度为0了,需要入栈
top = j + 1; //top指针加一
}
}
}
if(count < n){
printf("该图有回路.\n");
}
else{
printf("该图没有回路.\n");
}
}
int main()
{
ALGraph G;
CreateALGraph(&G);
TopologicalSort(&G,G.vexnum);
return 0;
} 验证部分
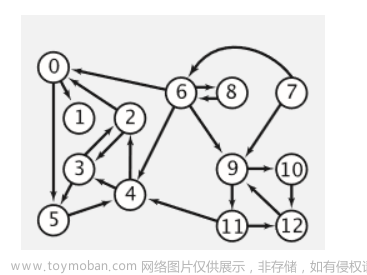
现在我们考虑下面这个例子:

很显然该图是无环的。
运行结果:

我们再看这个例子:

很显然这个图是有环的。
运行结果:
 文章来源:https://www.toymoban.com/news/detail-721339.html
文章来源:https://www.toymoban.com/news/detail-721339.html
符合我们的要求。文章来源地址https://www.toymoban.com/news/detail-721339.html
到了这里,关于数据结构-拓扑排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!