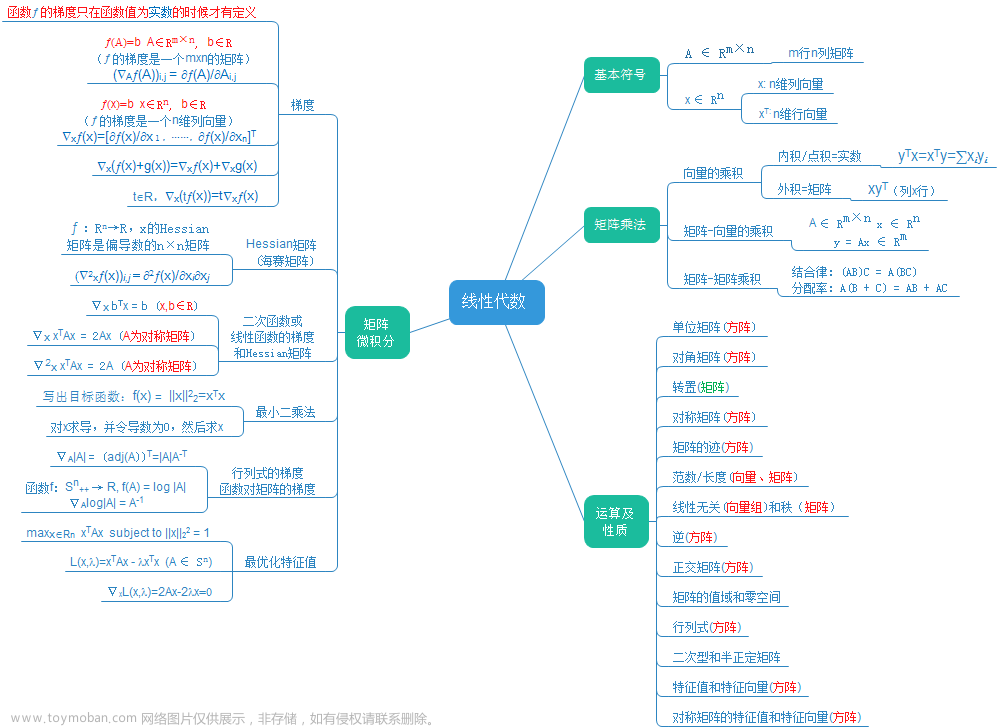
线性代数：基础解系

线性代数：基础解系

线性代数是大学数学中非常重要的一门课程。它包括向量空间、线性映射、矩阵、行列式、特征值和特征向量等内容。其中，基础解系是线性代数中非常基础的一个概念，也是后续许多内容的基础。

一、基础解系的定义

1.1 齐次线性方程组

我们先回顾一下齐次线性方程组的概念。齐次线性方程组由 $m$ 个线性方程组成，每个方程有 $n$ 个未知数，形如

$$\{\begin{array}{l}{a}_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n=0\\ a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n=0\\ ⋮\\ a_{m1}{x}_1+a_{m2}{x}_2+\cdots +a_{mn}{x}_n=0\end{array}$$

设 $\mathbf{x}=(x_1,x_2,\cdots ,x_n{)}^T$，${\mathbf{a}}_i=(a_{i1},a_{i2},\cdots ,a_{in}{)}^T$，则上述齐次线性方程组可以用矩阵和向量的形式表示为 $A\mathbf{x}=0$，其中

A = ( a 1 T a 2 T ⋮ a m T ) , x = ( x 1 x 2 ⋮ x n ) , 0 = ( 0 0 ⋮ 0 ) A=\begin{pmatrix}\boldsymbol{a}_1^T\\\boldsymbol{a}_2^T\\\vdots\\\boldsymbol{a}_m^T\end{pmatrix},\quad \boldsymbol{x}=\begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix},\quad \boldsymbol{0}=\begin{pmatrix}0\\0\\\vdots\\0\end{pmatrix} A= ​a1T​a2T​⋮amT​​ ​,x= ​x1​x2​⋮xn​​ ​,0= ​00⋮0​ ​

1.2 非零解和基础解系

如果存在一组非零向量 { x 1 , x 2 , ⋯   , x s } \{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} {x1​,x2​,⋯,xs​}，它们满足 $A{\mathbf{x}}_i=0$，则称 { x 1 , x 2 , ⋯   , x s } \{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} {x1​,x2​,⋯,xs​} 为齐次线性方程组 $A\mathbf{x}=0$ 的一个基础解系（或称为零空间的一组基）。

这里所说的“非零向量”，指的是所有分量均不为 $0$ 的向量。而“基础解系”则是指一个向量组，它们是该方程组的解向量，且任何一个解向量都可以由它们线性组合得到。

如果一个向量组 { x 1 , x 2 , ⋯   , x s } \{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} {x1​,x2​,⋯,xs​} 是齐次线性方程组 $A\mathbf{x}=0$ 的基础解系，则其余的解向量可以用 { x 1 , x 2 , ⋯   , x s } \{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} {x1​,x2​,⋯,xs​} 线性表示出来。设 $\mathbf{x}$ 是 $A\mathbf{x}=0$ 的任意一个解向量，则

$$\mathbf{x}=k_1{\mathbf{x}}_1+k_2{\mathbf{x}}_2+\cdots +k_s{\mathbf{x}}_s$$

其中 $k_1,k_2,\cdots ,k_s$ 是任意常数。

1.3 求解基础解系的方法

求解基础解系的方法有很多，这里介绍几种常见的方法。

1.3.1 列主元法

列主元法是求解基础解系的一种简单有效的方法。它的基本思想是：将增广矩阵进行初等行变换，得到一个行简化阶梯矩阵，然后找出主元列所对应的未知量，所得到的未知量就是基础解系中的一个向量。

具体步骤如下：

1. 将增广矩阵 $[A|0]$ 进行初等行变换，将其化为行简化阶梯矩阵；
2. 找出主元列对应的未知量，若该未知量出现在第 $r$ 行，则基础解系中应该有一个向量 ${\mathbf{x}}^{(r)}$，其前 $r-1$ 个分量为 $0$，第 $r$ 个分量为 $1$，其余分量为 $0$；
3. 重复步骤 2，直到所有主元列对应的向量都求得。

1.3.2 高斯-约旦消元法

高斯-约旦消元法是另一种常用的求解基础解系的方法。它的基本思想是：将增广矩阵化为行简化阶梯矩阵，然后从最后一行开始，依次求解每个未知量，得到其在基础解系中所对应的向量。

具体步骤如下：

1. 将增广矩阵 $[A|0]$ 进行初等行变换，将其化为行简化阶梯矩阵；
2. 从最后一行开始，依次求解每个未知量，得到一个解向量，若有 $k$ 个自由变量，则可以得到 $k$ 个解向量，它们构成了基础解系。

二、基础解系的性质

2.1 基础解系的个数和维数

齐次线性方程组 $A\mathbf{x}=0$ 的基础解系的个数和非基础解的个数相等，它们的和为未知量的个数 $n$。换句话说，基础解系的个数是 $(n-r)$，其中 $r$ 是 $A$ 的秩。

基础解系的向量个数称为零度（nullity）或自由度（degree of freedom），记为 $\mathrm{null}(A)$ 或 $\dim \ker (A)$，则有

$$\mathrm{null}(A)=n-\mathrm{rank}(A)$$

2.2 基础解系所在子空间

设 { x 1 , x 2 , ⋯   , x s } \{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} {x1​,x2​,⋯,xs​} 是齐次线性方程组 $A\mathbf{x}=0$ 的一个基础解系， span ⁡ { x 1 , x 2 , ⋯   , x s } \operatorname{span}\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} span{x1​,x2​,⋯,xs​} 表示由它们张成的向量空间，则有

ker ⁡ ( A ) = span ⁡ { x 1 , x 2 , ⋯   , x s } \ker(A)=\operatorname{span}\{\boldsymbol{x}_1,\boldsymbol{x}_2,\cdots,\boldsymbol{x}_s\} ker(A)=span{x1​,x2​,⋯,xs​}

这意味着，所有使得 $A\mathbf{x}=0$ 的 $\mathbf{x}$ 构成了一个向量空间，即零空间或核（kernel）。

2.3 基础解系与非奇异矩阵

如果矩阵 $A$ 是可逆矩阵，则只有零向量是其基础解系中的一个元素，换句话说，$\mathrm{null}(A)=0$。这是因为如果 $A\mathbf{x}=0$，则乘上 $A^{-1}$，得到 $\mathbf{x}=0$。

三、总结

基础解系是线性代数中非常基础的概念，也是后续许多内容的基础。本文介绍了基础解系的定义、求解方法和性质，希望可以对大家理解和掌握线性代数的基础知识有所帮助。文章来源地址https://www.toymoban.com/news/detail-721351.html

到了这里，关于线性代数：基础解系的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！