【人工智能】— 深度优先搜索、代价一致搜索、深度有限搜索、迭代深度优先搜索、图搜索-Toy模板网

这篇具有很好参考价值的文章主要介绍了【人工智能】— 深度优先搜索、代价一致搜索、深度有限搜索、迭代深度优先搜索、图搜索。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

什么是搜索

搜索问题是指既不能通过数学建模解决，又没有其他算法可以套用或者非遍历所有情况才能得出正确结果。这时就需要采用搜索算法来解决问题。搜索就是一种通过穷举所有解的状态，来求得题目所要求的解或者最优解的方法。
搜索的基本概念：
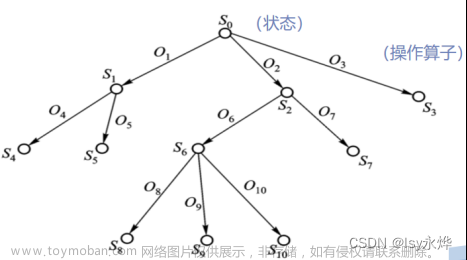
1. 状态：对某一系统在某一时刻的数学描述。
2. 动作：从当前时刻状态转移到下一时刻所处状态的操作。
3. 状态转移：对某一时刻的状态进行动作后所达到的状态。
4. 路径：一个状态序列，该序列被一系列动作所连接。
5. 目标测试：评估当前状态是否是所求解的目标状态。

树搜索算法

基本思想：通过扩展已探索状态的后继，离线模拟探索状态空间
以下图举例
根据给定的初始状态初始化搜索树
根据策略strategy决定扩展哪个叶子结点，直到达到目标状态

搜索策略

通过选择节点扩展的顺序来定义搜索策略
根据以下维度评估策略：
- 完整性(完备性）: 如果存在，它是否总能找到解决方案？
- 时间复杂性(时间复杂度）: 生成的节点数
- 空间复杂性(空间复杂度） : 内存中的最大节点数
- 最优性(最优性）: 它总是找到成本最低的解决方案吗？
时间和空间复杂性是根据
- b： maximum branching factor of the search tree搜索树的最大分支因子—分支因子
- d： depth of the least-cost solution—最浅的目标节点的深度
- m： maximum depth of the state space状态空间的最大深度（可以是 $\infty$ ）—最大深度

无信息搜索

不一致的搜索策略只使用问题定义中可用的信息

Breadth-first search 广度优先搜索
Uniform-cost search 代价一致搜索
Depth-first search 深度优先搜索
Depth-limited search 深度受限搜索
Iterative deepening search 迭代深度优先搜索

Breadth-first search

一致代价搜索,人工智能,人工智能,搜索

扩展最浅的未扩展节点
实施：边缘结点是一个FIFO队列，即，新来的后继放在末尾
时间复杂度：BFS算法的时间复杂度可以通过BFS中遍历的节点数来获得，直到最浅的节点。其中 d= 最浅解的深度，b是每个状态的节点。
空间复杂度： $O(b ^{d+1})$ (keeps every node in memory)
完整性：BFS完成，这意味着如果最浅的目标节点处于某个有限的深度，那么BFS将找到解决方案。
最优性：如果路径成本是节点深度的非递减函数，则BFS是最优的。
空间是个大问题；可以轻松地以100MB/秒的速度生成节点，因此24小时=8640GB。

Uniform-cost search

一致代价搜索(Uniform Cost Search)，优先扩展拥有最小路径消耗函数g(n)的结点，和最佳优先搜索(Best-first Search)在代码实现上一致，即最佳优先搜索的评价函数f(n)等于g(n)时，最佳优先搜索即为一致代价搜索。
一致代价搜索是用于遍历加权树或图的搜索算法。
当每个边缘有不同的成本时，该算法开始起作用。
一致代价搜索的主要目标是找到具有最低累积成本的目标节点的路径。一致代价搜索根据路径成本从根节点扩展节点。
它可用于解决需要最优成本的任何图/树。一致代价搜索算法由优先级队列实现。它最优先考虑最低累积成本。
如果所有边的路径成本相同，则一致代价搜索等效于宽度优先搜索算法。
完整性：是，如果每一步代价 $\geq ε$ 。
时间复杂性： $O (b ce i l in g (C * / ε)$ ， $C *$ 是最佳解决方案的成本， $g \leq$ 最优解代价的节点数
空间复杂度： $O (b ce i l in g (C * / ε)$ ， $g \leq$ 最优解代价的节点数
最优解：节点按 g(n) 的递增顺序扩展

Depth-first search

DFS的核心是沿着树的深度遍历树的结点，尽可能深的探索树的分支，当结点v的所有边都已经被探索后，将回溯到发现v的那条边的起始结点。这一过程一直进行到已发现初始结点可以到达的所有结点为止，如果还有未被发现的结点，则从中选择一个作为初始结点重复上述过程，直到所有结点都被访问为止。
DFS的基本原则可以归纳为：按照某种条件一直往前探索，如果在过程中失败，比如死路(全部探索完但是仍没有解)则返回，另选一条道路继续，直到到达目标结点为止。
深度优先搜索扩展搜索树中深度最深的结点。
它既不是完备的也不是最优的，但它具有线性的空间复杂度。
总是扩展在队列frontier中level最深的结点。深度优先搜索的其中一个variant是回溯搜索(Backtracking Search)，可以实现更小内存开销。
完整性：DFS搜索算法在有限状态空间内完成，因为它将扩展有限搜索树中的每个节点。
时间复杂度：DFS的时间复杂度将等同于算法遍历的节点。它的公式如下：

其中，m = 任何节点的最大深度，这可能远大于d(Shallowest解算深度)
空间复杂度：DFS算法只需要存储来自根节点的单个路径，因此DFS的空间复杂度等于边缘集的大小，即O(bm)。
最优解：DFS搜索算法不是最优的，因为它可能产生大量步骤或高成本以到达目标节点。

depth-limited search

深度受限搜索(Depth-limited Search)，是在深度优先搜索基础上，设置搜索深度限制。因为当搜索状态空间很大的时候，深度优先搜索DFS会非常尴尬，所以可以通过设置搜索深度界限来避免。
深度有限搜索算法类似于具有预定限制的深度优先搜索。深度限制搜索可以解决深度优先搜索中无限路径的缺点。在该算法中，深度限制的节点将被视为没有后继节点。
可以使用两个失败条件终止深度限制搜索：
- 标准故障值：表示问题没有任何解决方案。
- 截止故障值：它在给定的深度限制内没有定义问题的解决方案。
完整性：如果解决方案高于深度限制，则DLS搜索算法完成。
时间复杂度：DLS算法的时间复杂度为O(bℓ)。
空间复杂度：DLS算法的空间复杂度为O(b×l)。
最优解：深度限制搜索可以看作是DFS的一个特例，即使ℓ> d也不是最优的。

Iterative deepening search

由Depth-limited search演化而成，每轮增加深度限制
迭代加深的深度优先搜索(Iterative deepening depth-first Search)，逐步增大限制搜索的深度，直到返回目标结点。

迭代加深的深度优先搜索是DFS和BFS算法的组合。此搜索算法找出最佳深度限制，并通过逐渐增加限制直到找到目标为止。迭代加深（Iterative deepening）搜索，实质上就是限定下界的深度优先搜索。即首先允许深度优先搜索K层搜索树，若没有发现可行解，再将K+1后重复以上步骤搜索，直到搜索到可行解。

在迭代加深搜索的算法中，连续的深度优先搜索被引入，每一个深度约束逐次加1，直到搜索到目标为止。

迭代加深搜索算法就是仿广度优先搜索的深度优先搜索。既能满足深度优先搜索的线性存储要求，又能保证发现一个最小深度的目标结点。

从实际应用来看，迭代加深搜索的效果比较好，并不比广度优先搜索慢很多，但是空间复杂度却与深度优先搜索相同，比广度优先搜索小很多，在一些层次遍历的题目中，迭代加深不失为一种好方法！

该算法执行深度优先搜索直到某个“深度限制”，并且在每次迭代之后它不断增加深度限制，直到找到目标节点。

此搜索算法结合了广度优先搜索的快速搜索和深度优先搜索的内存效率的优势。当搜索空间很大并且目标节点的深度未知时，迭代搜索算法对于无知搜索是有用的。

示例，以下树结构显示迭代加深深度优先搜索。IDDFS算法执行各种迭代，直到找到目标节点。算法执行的迭代如下
第1次迭代——-> A
第2次迭代——> A，B，C
第3次迭代———> A，B，D，E，C，F，G
第4次迭代———> A，B，D，H，I，E，C，F，K，G
在第四次迭代中，算法将找到目标节点。
完整性：如果分支因子是有限的，则该算法是完整的。
时间复杂性：假设b是分支因子，深度是d，那么最坏情况时间复杂度是O(b^d)。
空间复杂性：IDDFS的空间复杂度为O(bd)。
最优解：如果路径成本是节点深度的非递减函数，则IDDFS算法是最佳的。