1. Toy模板网首页
  2. > Toy博客

Java数据结构与算法----动态规划（背包篇）

9月前 作者：stu_kk 分类：Toy博客 阅读(48) 违法举报

这篇具有很好参考价值的文章主要介绍了Java数据结构与算法----动态规划（背包篇）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 0/1背包

1.1.算法思路

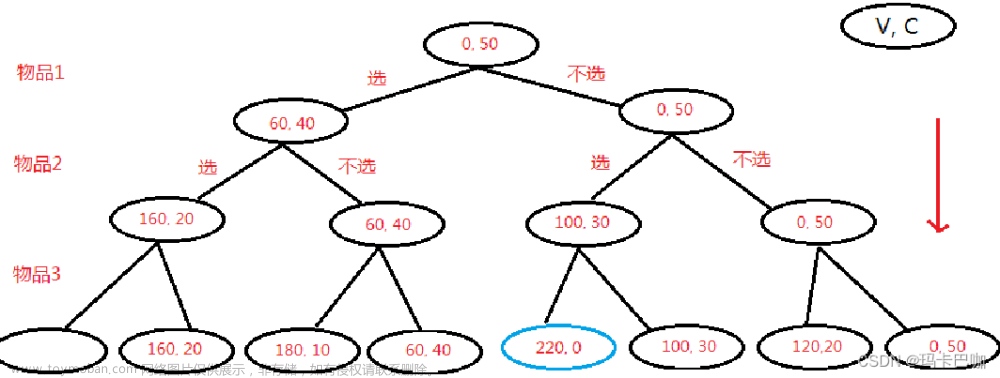
0/1背包是动态规划、背包问题中最经典的问题啦！它主要的问题是：

给定n种物品、这n种物品的重量分别是，价值分别是 ，而你有一个容量为C的背包，请问如何求出所能拿的最大价值呢？

对于动态规划，我们先需要找到一条推导公式，然后确定边界：

我们设dp[i][j]为一个背包，表示前 i 个物品装入容器为 j 的背包中可以获得的最大价值。

我们可以推导出： dp[i] [j] = max(dp[i-1] [j] , dp[i-1] [j -  ] +  ) 也就是说，当前的dp值由装和不装入第i个物品来决定的。不装入第i个是：dp[i-1] [j] ，装入的话 j 要减去这个物品的重量也就是：

  dp[i-1] [j -  ] +  。

1.2.例题与代码

01背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i 件物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi , wi 用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

8

 题解：

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 0:19
 **/
public class Main {
    private static BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
    private static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    public static void main(String[] args) {
        int n,v;//物品数量、容积
        int value[] = new int[1001];
        int weight[] = new int[1001];
        Scanner cin = new Scanner(System.in);
        n = cin.nextInt();
        v = cin.nextInt();
        int dp[][] = new int[n+1][v+1];
        for(int i = 1;i<=n;i++) {
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
        }
        //输入完毕。
        for(int i = 1;i<=n;i++) {
            for(int j = 0;j<=v;j++){
                if(j < weight[i]){
                    dp[i][j] = dp[i-1][j];
                }
                else{
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i]);
                }
            }
        }
        System.out.println(dp[n][v]);
    }
}

优化：

其实可以用dp[] 来替代 dp[][]以节省空间，因为i只跟上一行有关系，跟更前面的没关系，所以用新的一行覆盖上一行就ok了。

import java.util.*;
import java.math.*;
public class Main {

	public static void main(String[] args) {
		// TODO 自动生成的方法存根
		int n,v;//物品数量、容积
		int value[] = new int[10001];
		int weight[] = new int[10001];
		int dp[] = new int[10001];
		Scanner cin = new Scanner(System.in);
		n = cin.nextInt();
		v = cin.nextInt();
		for(int i = 1;i<=n;i++) {
			weight[i] = cin.nextInt();
			value[i] = cin.nextInt();
		}
		//输入完毕。
		for(int i = 1;i<=n;i++) {
			for(int j =v;j>=weight[i];j--) {
				dp[j] = Math.max(dp[j],(dp[j-weight[i]]+value[i]));
			}
		}
		System.out.println(dp[v]);
	}
}

2.完全背包

2.1.算法思路

完全背包和0/1背包只有一个区别，那就是0/1背包的物品数量只有1，只可以被装1次，而完全背包的物品数量无数，可以装多次。

在代码上，我们只需要将0/1背包的j循环换一下方向就行了：

2.2.例题与题解

完全背包问题

有 N种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值。

输入格式

第一行两个整数，N，V 用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行两个整数 vi,wi，用空格隔开，分别表示第 i种物品的体积和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 5

输出样例：

10

题解：

import java.util.Scanner;
/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 0:40
 **/
public class Main {
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int weight[] = new int[n+1];
        int value[] = new int[n+1];
        int dp[] = new int[v+1];
        for(int i = 1;i <= n;i++){
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
        }
        for(int i = 1;i<=n;i++){
            for(int j = weight[i]; j<=v;j++){
                dp[j] = Math.max(dp[j],dp[j-weight[i]] + value[i]);
            }
        }
        System.out.println(dp[v]);
    }
}

3.多重背包

3.1.算法思想

多重背包和完全背包、0/1背包只有一点区别，那就是多重背包设置了物品的数量了，（完全背包的物品有无数个，0/1背包的有一个）因此，我们需要在0/1背包的基础上加上数量的循环判断装与不装。而且它存在优化，我们在后面的优化会说到。

3.2.例题与题解

多重背包问题 I

有 N种物品和一个容量是 V 的背包。

第 i种物品最多有 si件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V 用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si 用空格隔开，分别表示第 i 种物品的体积、价值和数量。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤100
0<vi,wi,si≤100

输入样例

4 5
1 2 3
2 4 1
3 4 3
4 5 2

输出样例：

10

这个题的数量级只有100，不需要优化

import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 0:54
 **/
public class Main {
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int weight[] = new int[n+1];
        int value[] = new int[n+1];
        int count[] = new int[n+1];
        int dp[] = new int[v+1];
        for(int i = 1;i<=n;i++){
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
            count[i] = cin.nextInt();
        }
        for(int i = 1;i<=n;i++){
            for(int j = v;j>=0;j--){
                for(int k = 0;k<=count[i] && j >= k*weight[i] ;k++){
                    dp[j] = Math.max(dp[j],dp[j - k*weight[i]] + k*value[i]);
                }
            }
        }
        System.out.println(dp[v]);
    }
}

优化：

对于多重背包，上面的做法是三重循环，复杂度肯定太高了啊，我们尝试把他变成0/1背包，怎么变成0/1背包呢？ 我们看：dp[j] = Math.max(dp[j],dp[j - k*weight[i]] + k*value[i]);这里的公式贼像0/1背包啊，我们尝试把count个物品用二进制表示：

假设：8个物品：二进制表示为 1000 ，对于装这个物品的使用情况会有：1 、2、3、4、5、6、7、8这8种情况，其实这些数字 可以由1  2  4 这三个数字组合成，对于n可以被分解成1,2,4,…,2^(k-1),n-2^k+1。然后把他们保存起来：进行0/1背包计算最大值就ok!

import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 1:14
 **/
public class Main {
    private static class stu{
        int weight;
        int value;

        public stu(int weight, int value) {
            this.weight = weight;
            this.value = value;
        }
    }
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int dp[] = new int[v+1];
        List<stu> list = new LinkedList<>();
        for(int i = 1;i<=n;i++) {
            int weight = cin.nextInt();
            int value = cin.nextInt();
            int count = cin.nextInt();
            for(int j = 1;j <= count;j*=2){
                list.add(new stu(j*weight,j*value));
                count -= j;
            }
            if(count > 0){
                list.add(new stu(count*weight,count*value));
            }
        }
        for(stu s : list){
            for(int j = v;j>=s.weight;j--){
                dp[j] = Math.max(dp[j],dp[j-s.weight] + s.value);
            }
        }
        System.out.println(dp[v]);
    }
}

4.混合背包

4.1.算法思想

混合背包，所谓混合，就是包含了0/1背包、完全背包和多重背包，我们可以直接使用多重背包的二进制优化进行写。把01背包看作是数量为1的多重别抱，完全背包看成是数量为无数的多重背包就好了。

4.2.例题与题解

混合背包问题

有 N 种物品和一个容量是 V 的背包。

物品一共有三类：

  • 第一类物品只能用1次（01背包）；
  • 第二类物品可以用无限次（完全背包）；
  • 第三类物品最多只能用 si 次（多重背包）；

每种体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。

输入格式

第一行两个整数，N，V ，用空格隔开，分别表示物品种数和背包容积。

接下来有 N 行，每行三个整数 vi,wi,si 用空格隔开，分别表示第 i 种物品的体积、价值和数量。

  • si=−1 表示第 i 种物品只能用1次；
  • si=0 表示第 i 种物品可以用无限次；
  • si>0 表示第 i 种物品可以使用 si 次；

输出格式

输出一个整数，表示最大价值。

数据范围

0< N,V ≤1000
0< vi,wi ≤1000
−1≤ si ≤1000

输入样例

4 5
1 2 -1
2 4 1
3 4 0
4 5 2

输出样例：

8
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 10:10
 **/
public class Main {
    private static class stu{
        int weight;
        int value;

        public stu(int weight, int value) {
            this.weight = weight;
            this.value = value;
        }
    }
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int dp[] = new int[v+1];
        List<stu> list = new LinkedList<>();
        for(int i = 1;i<=n;i++){
            int weight = cin.nextInt();
            int value = cin.nextInt();
            int s = cin.nextInt();
            if(s == -1){
                list.add(new stu(weight,value));
            }
            else if(s == 0){
                for(int j = 1;j*weight <= v;j*=2 ){
                    list.add(new stu(j*weight,j*value));
                }
            }
            else{
                for(int j = 1;j<=s && j*weight<=v;j*=2){
                    list.add(new stu(j*weight,j*value));
                    s -= j;
                }
                if(s > 0){
                    list.add(new stu(s*weight,s*value));
                }
            }
        }
        for(stu s : list){
            for(int j = v;j>=s.weight;j--){
                dp[j] = Math.max(dp[j],dp[j - s.weight] + s.value);
            }
        }
        System.out.println(dp[v]);
    }
}

5.二位费用背包

5.1.算法思想

二位费用背包其实就是在01背包的基础上再加上一个条件限制，比如在背包中加上体积、重量这两个限制，也就是变成二维了。我们需要把dp数组变成二维的，用来代表体积、重量的背包。

5.2.例题与题解

二维费用的背包问题

有 N 件物品和一个容量是 V 的背包，背包能承受的最大重量是 M。

每件物品只能用一次。体积是 vi，重量是 mi，价值是 wi。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，总重量不超过背包可承受的最大重量，且价值总和最大。
输出最大价值。

输入格式

第一行三个整数，N,V,M，用空格隔开，分别表示物品件数、背包容积和背包可承受的最大重量。

接下来有 N 行，每行三个整数 vi,mi,wi，用空格隔开，分别表示第 i 件物品的体积、重量和价值。

输出格式

输出一个整数，表示最大价值。

数据范围

0<N≤1000
0<V,M≤100
0<vi,mi≤100
0<wi≤1000

输入样例

4 5 6
1 2 3
2 4 4
3 4 5
4 5 6

输出样例：

8

import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 10:56
 **/
public class Main {

    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int m = cin.nextInt();
        int vi[] = new int[n+1];
        int weight[] = new int[n+1];
        int value[] = new int[n+1];

        for(int i = 1;i<=n;i++){
            vi[i] = cin.nextInt();
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
        }
        int dp[][] = new int[v+1][m+1];
        for(int i = 1;i<=n;i++){
            for(int j = v;j>=vi[i];j--){
                for(int k = m;k>= weight[i];k--){
                    dp[j][k] = Math.max(dp[j][k],dp[j-vi[i]][k - weight[i]] + value[i]);
                }
            }
        }
        System.out.println(dp[v][m]);
    }
}

6.分组背包

6.1.算法思想

分组背包和01背包的区别就是，给定的物品是有分组的，每一组的物品最多只可以用一种。我们可以循环遍历一下每一组物品，进行01背包的操作。

6.2.例题与题解

分组背包问题

有 N 组物品和一个容量是 V 的背包。

每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij ，价值是 wij ，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品组数和背包容量。

接下来有 N 组数据：

  • 每组数据第一行有一个整数 Si，表示第 i 个物品组的物品数量；
  • 每组数据接下来有 Si 行，每行有两个整数 vij,wij，用空格隔开，分别表示第 i 个物品组的第 j 个物品的体积和价值；

输出格式

输出一个整数，表示最大价值。

数据范围

0<N,V≤100
0<Si≤100
0<vij,wij≤100

输入样例

3 5
2
1 2
2 4
1
3 4
1
4 5

输出样例：

8
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 11:15
 **/
public class Main {
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int v = cin.nextInt();
        int weight[][] = new int[101][101];
        int value[][] = new int[101][101];
        int s[] = new int[101];
        int dp[][] = new int[101][101];
        for(int i = 1;i<=n;i++){
            s[i] = cin.nextInt();
            for(int j = 1;j<=s[i];j++){
                weight[i][j] = cin.nextInt();
                value[i][j] = cin.nextInt();
            }
        }
        for(int i = 1;i <= n;i++){
            for(int j = 0;j<=v;j++){
                dp[i][j] = dp[i-1][j];
                for(int k = 1;k<=s[i];k++){
                    if(j >= weight[i][k]){
                        dp[i][j] = Math.max(dp[i][j],dp[i-1][j - weight[i][k]] + value[i][k]);
                    }
                }
            }
//            for(int j = 1;j<=s[i];j++){
//                for(int k = weight[i][j];k<= v;k++){
//                    dp[i][k] = Math.max(dp[i][k],dp[i-1][k-weight[i][j]] + value[i][j]);
//                }
//            }
        }
        System.out.println(dp[n][v]);
    }
}

7.依赖背包

有依赖的背包问题

有 N 个物品和一个容量是 V 的背包。

物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点。

如下图所示：

java动态规划,动态规划,算法

如果选择物品5，则必须选择物品1和2。这是因为2是5的父节点，1是2的父节点。

每件物品的编号是 i ，体积是 vi，价值是 wi ，依赖的父节点编号是 pi 。物品的下标范围是 1…N1。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

输入格式

第一行有两个整数 N，V，用空格隔开，分别表示物品个数和背包容量。

接下来有 N 行数据，每行数据表示一个物品。
第 i 行有三个整数 vi,wi,pi ，用空格隔开，分别表示物品的体积、价值和依赖的物品编号。
如果 pi=−1，表示根节点。 数据保证所有物品构成一棵树。

输出格式

输出一个整数，表示最大价值。

数据范围

1≤N,V≤100
1≤vi,wi≤100

父节点编号范围：

  • 内部结点：1≤pi≤N1;
  • 根节点 pi=−1;

输入样例

5 7
2 3 -1
2 2 1
3 5 1
4 7 2
3 6 2

输出样例：

11
难度：困难
时/空限制：1s / 64MB
总通过数：15113
总尝试数：24316
来源：背包九讲
算法标签

挑战模式


import java.util.*;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-12 20:48
 **/
public class Main {
    private static int weight[],value[],root,dp[][],n,v;
    private static List<Integer> father[];
    public static void main(String[] args) {
        Scanner cin = new Scanner(System.in);
        n = cin.nextInt();
        v = cin.nextInt();
        weight = new int[n+1];
        value = new int[n+1];
        father = new List[n+1];
        dp = new int[n+1][v+1];
        for(int i = 1;i <= n;i++){
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
            int pi = cin.nextInt();
            if(pi == -1){
                root = i;
            }
            else{
                if(father[pi] == null){
                    father[pi] = new LinkedList<Integer>();
                }
                father[pi].add(i);
            }
        }
        dfs(root);
        System.out.println(dp[root][v]);
    }

    private static void dfs(int root) {
        for(int i = weight[root];i<=v;i++){
            dp[root][i] = value[root]; //放入这个节点
        }
        for(int i = 0;father[root] != null &&  i < father[root].size() ;i++){
            int to = father[root].get(i);
            dfs(to);
            for(int j = v;j>=weight[root];j--){
                for(int k = 0;k<= j - weight[root];k++){
                    dp[root][j] = Math.max(dp[root][j],dp[root][j - k] + dp[to][k]);
                }
            }
        }
    }
}

8.背包方案数

在01背包的基础上，使用一个数组用来保存方案数，如果最大价值相同，那么加上方案数量

背包问题求方案数

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。

第 i  件物品的体积是 vi ，价值是 wi 。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出 最优选法的方案数。注意答案可能很大，请输出答案模 109+7 的结果。

输入格式

第一行两个整数，N，V ，用空格隔开，分别表示物品数量和背包容积。

接下来有 N 行，每行两个整数 vi,wi 用空格隔开，分别表示第 i 件物品的体积和价值。

输出格式

输出一个整数，表示 方案数 模 109+7109+7 的结果。

数据范围

0<N,V≤1000
0<vi,wi≤1000

输入样例

4 5
1 2
2 4
3 4
4 6

输出样例：

2
package 背包;

import java.util.Arrays;
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-17 20:50
 **/
public class 背包方案 {
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int m = cin.nextInt();
        int mod = 1000000007;
        int weight[] = new int[n+1];
        int value[] = new int[n+1];
        for(int i = 1;i<=n;i++){
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
        }
        int dp[] = new int[m+1];
        long num[] = new long[m+1];
        Arrays.fill(num,1);
        for(int i = 1;i<=n;i++){
            for(int j = m;j >= weight[i]; j--){
                int pi = Math.max(dp[j],dp[j-weight[i]] + value[i]);
                long cnt = 0;
                if(pi == dp[j]){
                    cnt = (cnt %mod + num[j]%mod)%mod;
                }
                if(pi == (dp[j-weight[i]] + value[i])) {
                    cnt = (cnt%mod + num[j-weight[i]]%mod)%mod;
                }
                num[j] = cnt%mod;
                dp[j] = pi;
            }
        }
        System.out.println(num[m]);
    }
}

9.求背包具体方案

背包问题求具体方案文章来源地址https://www.toymoban.com/news/detail-722161.html

import java.util.Arrays;
import java.util.Scanner;

/**
 * @Author: stukk
 * @Description: TODO
 * @DateTime: 2023-04-17 21:26
 **/
public class Main {
    public static void main(String[] args) {
        Scanner cin  =new Scanner(System.in);
        int n = cin.nextInt();
        int m = cin.nextInt();
        int weight[] = new int[n+1];
        int value[] = new int[n+1];
        for(int i = 1;i<=n;i++){
            weight[i] = cin.nextInt();
            value[i] = cin.nextInt();
        }
        int dp[][] = new int[n+2][m+2];
        for(int i = n;i >= 1;i--){
            for(int j = 0;j <= m; j++){
                dp[i][j] = dp[i+1][j];
                if(j >= weight[i])
                    dp[i][j] = Math.max(dp[i][j],dp[i+1][j-weight[i]] + value[i]);
            }
        }
        int ans = m;
        for(int i = 1;i<=n;i++){
            if(ans >= weight[i] && dp[i][ans] == dp[i+1][ans - weight[i]] + value[i]){
                ans -= weight[i];
                System.out.print(i+" ");
            }
        }
    }
}

到了这里，关于Java数据结构与算法----动态规划（背包篇）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • Java数据结构与算法：动态规划之斐波那契数列

    大家好，我是免费搭建查券返利机器人赚佣金就用微赚淘客系统3.0的小编。在这寒冷的季节里，让我们一同探讨Java中的动态规划，重点关注解决问题的经典代表之一——斐波那契数列。 动态规划简介 动态规划是一种解决问题的数学方法，通常用于优化递归算法。它通过将问

    2024年01月22日
    浏览(47)
  • 数据结构与算法-动态规划

    数据结构与算法-动态规划

    （我猜是做的多了背的题多了就自然懂了） 迭代法一般没有通用去重方式,因为已经相当于递归去重后了 这两个问题其实是一个问题,一般直接写出的没有去重的递归法,复杂度很高,此时需要使用备忘录去重,而备忘录去重时间复杂度和使用dp数组进行迭代求解时间复杂度相同

    2024年02月04日
    浏览(43)
  • python算法与数据结构---动态规划

    python算法与数据结构---动态规划

    记不住过去的人，注定要重蹈覆辙。 对于一个模型为n的问题，将其分解为k个规模较小的子问题（阶段），按顺序求解子问题，前一子问题的解，为后一子问题提供有用的信息。在求解任一子问题时，通过决策求得局部最优解，依次解决各子问题。最后通过简单的判断，得到

    2024年02月20日
    浏览(65)
  • 数据结构与算法之贪心&动态规划

    数据结构与算法之贪心&动态规划

            一：思考         1.某天早上公司领导找你解决一个问题，明天公司有N个同等级的会议需要使用同一个会议室，现在给你这个N个会议的开始和结束 时间，你怎么样安排才能使会议室最大利用？即安排最多场次的会议？电影的话 那肯定是最多加票价最高的，入场

    2024年02月09日
    浏览(47)

  • 数据结构与算法 | 动态规划算法（Dynamic Programming）

    上一篇文末已经提到了记忆化搜索是动态规划（Dynamic Programming）的一种形式，是一种自顶向下（Top-Down）的思考方式，通常采用递归的编码形式；既然动态规划有自顶向下（Top-Down）的递归形式，自然想到对应的另外一种思考方式 自底向上（ Bottom-Up ） ，也就是本篇要写的内

    2024年02月05日
    浏览(44)

  • 数据结构与算法：动态规划（Dynamic Programming）详解

    动态规划（Dynamic Programming，简称DP） 是一种在数学、管理科学、计算机科学、经济学和生物信息学等领域中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划经常被用于求解优化问题。 动态规划的核心思想是将复杂问题分解为更小的子问

    2024年04月25日
    浏览(47)
  • python数据结构与算法-动态规划(最长公共子序列)

    python数据结构与算法-动态规划(最长公共子序列)

    一个序列的子序列是在该序列中删去若干元素后得 到的序列。 例如：\\\"ABCD”和“BDF”都是“ABCDEFG”的子序列。 最长公共子序列(LCS) 问题: 给定两个序列X和Y，求X和Y长度最大的公共子字列。 例:X=\\\"ABBCBDE”Y=\\\"DBBCDB”LCS(XY)=\\\"BBCD\\\" 应用场景:字符串相似度比对 （1）问题思考 思考: 暴

    2024年02月08日
    浏览(49)

  • 《python算法与数据结构2000讲》 动态规划深度剖析

    2024年01月12日
    浏览(48)
  • 【夜深人静学数据结构与算法 | 第十篇】动态规划

    【夜深人静学数据结构与算法 | 第十篇】动态规划

    目录 前言： 动态规划： 常见应用： 解题步骤：  动态规划的简化步骤： 案例： 509. 斐波那契数 - 力扣（LeetCode） 70. 爬楼梯 - 力扣（LeetCode） 62. 不同路径 - 力扣（LeetCode） 总结：         本文我们将为大家讲解一下动态规划的理论知识，并且会讲解几道力扣的经典例题。

    2024年02月11日
    浏览(50)
  • 【数据结构与算法】Kadane‘s算法（动态规划、最大子数组和）

    【数据结构与算法】Kadane‘s算法（动态规划、最大子数组和）

    Kadane\\\'s 算法是一种用于解决最大子数组和问题的动态规划算法。这类问题的目标是在给定整数数组中找到一个连续的子数组，使其元素之和最大（数组含有负数）。 算法的核心思想是通过迭代数组的每个元素，维护两个变量来跟踪局部最优解和全局最优解。 以下是Kadane’s算

    2024年03月22日
    浏览(98)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包