一、基本思路
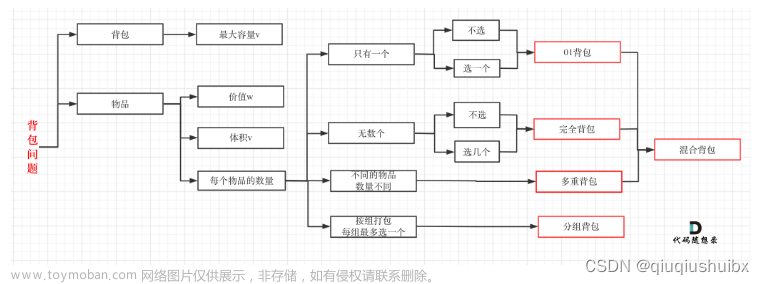
1、背包问题概述
- 0 1 背包问题:
-
- 条件:N 个物品容量为 V 的背包,每件物品最多用 1 次,其中物品信息体积为 Vi,价值为 Wi。
-
- 目标:选出物品,使价值最大(不一定装满背包)。
-
- 特点:每件物品最多只用 1 次
- 完全背包问题:
-
- 特点:每一件物品都有无限个
- 多重背包问题:
-
- 特点:每个物品有 si 个(有限个)
-
- 优化:当面对物品种类比较多的时候,复杂度较高,可以进行优化操作;DP优化一般是对动态规划的方程和代码做等价变形。
- 分组背包问题:
-
- 特点:有 N 组物品,每一组物品里面有 si 种物品,一组里面只能选择 1 个物品
2、动态规划(DP)问题分析
-
分析步骤:

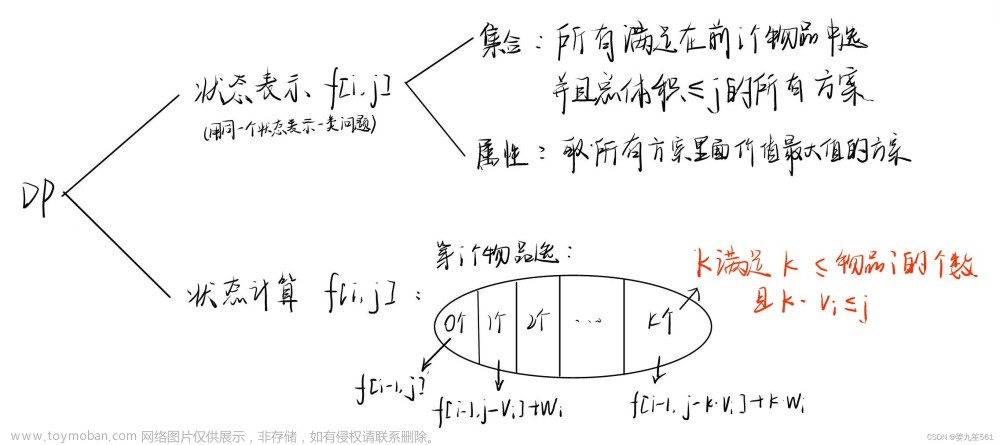
- 背包问题中的状态表示 f [ i , j ]:
-
- f [ N, V ] 表示所有从前 N 个物品中选,且总体积不超过 V 的选法集合, f [N, V]表示集合中每种选法总价值的最大值。
二、背包问题
1、0 1 背包问题
- 集合划分:

- 一维优化:
- 将 f 的第一个维度优化掉,但是需要注意是否使用到 f [ i - 1 ][] 也就是前面一层的数值,使用到的话就需要进行倒序遍历,否则会发生更新。

// 因为左边的j是由右边的j更新过来的,所以替换成一维还是用的上一层i-1的j
// f[j] = f[j]; // 左边不包含i的方案
// f[i][j] = f[i-1][j];
// f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
// 因为我们的f[i][j]是由f[i - 1][j]更新过来的,
// 替换成一维之后,需要保证f[j]是由(i - 1)层的f[j - v[i]]更新的
// 又因为(j - v[i]) 严格小于j的,
// 所以f[j - v[i]]肯定是在f[j]之前被求出,我们如果是从小到大枚举的j的话
// 如果有可能枚举到(j - v[i])是在我们当前 i 层中求出过,那就表示是这一层的值,我们要的是上一层的值
//f[2] = f[2 - 2] = f[0]
//f[3] = f[3 - 2] = f[1]
//f[4] = f[4 - 2] = f[2],这时候的f[2]在我们这一层中更新过,所以用的是我们这一层的值,我们要的是上一层的值
//所以我们需要一共逆序遍历j
//f[9] = f[9 - 3]
//f[8] = f[8 - 3]
//f[7] = f[7 - 3]
//...
//f[3] = f[3 - 3],可以看出没有一个是重复出现的,所以这个时候用的就是上一层的值,《等价变形》
//f[j] = Math.max(f[j] , f[j - v[i]] + w[i]); //右边包含i的方案,f[i-1][j - v[i]] + w[i]
2、完全背包问题
-
思路分析:

-
集合划分:

-
思路优化:

3、多重背包问题
- 思路分析:

- 集合划分:
-
此处是暴力做法,对于物品 0 < NV ≤ 100 ,0 < vi,wi,si ≤ 100 满足,假如数据表达则复杂度较高。

- 思路优化——二进制优化:
- 主要思想是将 si 进行分解,使用二进制进行表示。
- 注意此种方法主要是处理 物品种类 N 数值较大,导致的的计算复杂度较大的问题。


4、分组背包问题
- 思路分析:

- 集合划分:

三、例题题解

// java题解实现
// f[i][j] 方阵形式————朴素形式
// 将所要求的属性,进行集合划分
import java.util.*;
import java.io.*;
public class Main{
static int N = 1010;
static int[] v = new int[N]; // 每件物品体积
static int[] w = new int[N]; // 每件物品价值
static int[][] f = new int[N][N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m; // n为件数,m为背包体积
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
f[i][j] = f[i - 1][j]; // 不含有第i件物品的最大价值
if(j >= v[i]){ // 判断是否能加入背包,如果物品体积比背包大,那就加入不了
f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
// 含有第i件物品的最大价值,求解max
// 求解最大的时候暗含一个逻辑,就是之前没加vi已经能存多少了,和加了vi(有可能只剩下i)进行比较
// 看看哪一个多,是多个小件总价值大,还是一个大件价值大
}
}
}
System.out.println(f[n][m]);
}
}
// 一维优化做法
import java.util.*;
import java.io.*;
public class Main{
static int N = 1010;
static int[] v = new int[N]; // 每件物品体积
static int[] w = new int[N]; // 每件物品价值
static int[] f = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m; // n为件数,m为背包体积
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
}
for(int i = 1; i <= n; i++){
for(int j = m; j >= v[i]; j--){
f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
//因为左边的j是由右边的j更新过来的,所以替换成一维还是用的上一层i-1的j
//f[j] = f[j]; // 左边不包含i的方案
//f[i][j] = f[i-1][j];
// f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]] + w[i]);
//因为我们的f[i][j]是由f[i - 1][j]更新过来的,
//替换成一维之后,需要保证f[j]是由(i - 1)层的f[j - v[i]]更新的
//又因为(j - v[i]) 严格小于j的,
//所以f[j - v[i]]肯定是在f[j]之前被求出,我们如果是从小到大枚举的j的话
//如果有可能枚举到(j - v[i])是在我们当前 i 层中求出过,那就表示是这一层的值,我们要的是上一层的值
//f[2] = f[2 - 2] = f[0]
//f[3] = f[3 - 2] = f[1]
//f[4] = f[4 - 2] = f[2],这时候的f[2]在我们这一层中更新过,所以用的是我们这一层的值,我们要的是上一层的值
//所以我们需要一共逆序遍历j
//f[9] = f[9 - 3]
//f[8] = f[8 - 3]
//f[7] = f[7 - 3]
//...
//f[3] = f[3 - 3],可以看出没有一个是重复出现的,所以这个时候用的就是上一层的值,《等价变形》
//f[j] = Math.max(f[j] , f[j - v[i]] + w[i]); //右边包含i的方案,f[i-1][j - v[i]] + w[i]
}
}
System.out.println(f[m]);
}
}

// 完全背包问题
// 朴素算法
import java.util.*;
import java.io.*;
public class Main{
static int N = 1010;
static int[] v = new int[N]; // 每件物品体积
static int[] w = new int[N]; // 每件物品价值
static int[][] f = new int[N][N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m; // n为件数,m为背包体积
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
for(int k = 0; k * v[i] <= j; k++){ // 选择 k 个第 i 个物品
f[i][j] = Math.max(f[i][j], f[i - 1][j - v[i]*k] + w[i] * k);
}
}
}
System.out.println(f[n][m]);
}
}
// 完全背包问题
// 进一步推导的结果
import java.util.*;
import java.io.*;
public class Main{
static int N = 1010;
static int[] v = new int[N]; // 每件物品体积
static int[] w = new int[N]; // 每件物品价值
static int[][] f = new int[N][N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m; // n为件数,m为背包体积
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
f[i][j] = f[i- 1][j];
if(j >= v[i]){
f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]); // 进一步推导
}
}
}
System.out.println(f[n][m]);
}
}
// 完全背包问题
// 一维优化
import java.util.*;
import java.io.*;
public class Main{
static int N = 1010;
static int[] v = new int[N]; // 每件物品体积
static int[] w = new int[N]; // 每件物品价值
static int[] f = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m; // n为件数,m为背包体积
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
}
for(int i = 1; i <= n; i++){
for(int j = v[i]; j <= m; j++){
f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
}
}
System.out.println(f[m]);
}
}

// 多重背包问题
// 朴素写法
import java.util.*;
import java.io.*;
public class Main{
static int N = 110;
static int[] v = new int[N];
static int[] w = new int[N];
static int[] s = new int[N];
static int[][] f = new int[N][N];
public static void main(String[] args) throws IOException{
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
int n,m;
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
v[i] = Integer.parseInt(str2[0]);
w[i] = Integer.parseInt(str2[1]);
s[i] = Integer.parseInt(str2[2]);
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
for(int k = 0; k <= s[i] && k * v[i] <= j; k++){ // 相对完全背包问题,此处对k增加了限制
f[i][j] = Math.max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
}
}
}
System.out.println(f[n][m]);
}
}
 文章来源:https://www.toymoban.com/news/detail-722426.html
文章来源:https://www.toymoban.com/news/detail-722426.html
// 多重背包问题————二进制优化算法
// 主要思路:
// 1、将N种物品中的每种物品(每种s件),拆分成 N * log(s) 种(将s进行二进制表示尽心拆分)
// 2、对于这N * log(s) 种物品,每种物品只存在选择,还是不选择两种情况,也就意味转化为01背包问题
// 注意:
// 1、进行s拆分的时候,一定也要考虑二进制代表的v、w的会随着二进制数的大小进行翻倍
// 2、s拆分完毕之后,每一种的选择与否由01背包决定
// 3、我们在进行vw存储的时候,每一个都代表了一种s选择方式,但实际上i没有实际意义,只是将s进行拆分后的结果。
import java.util.*;
import java.io.*;
public class Main{
static int n,m;
static int N = 12000;
static int[] v = new int[N];
static int[] w = new int[N];
static int[] f = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
int count = 0; // count是为了记录s拆分为二进制后,新的拆分数量
for(int i = 1; i <= n; i++){
String[] str2 = in.readLine().split(" ");
int vi = Integer.parseInt(str2[0]);
int wi = Integer.parseInt(str2[1]);
int si = Integer.parseInt(str2[2]);
// 将si进行二进制拆分,拆分成logs种新的物品(每种只有一件)
int k = 1; // 此处相当于是2的0次幂
while(si >= k){
count++; // 新拆分了一种方法
v[count] = vi * k;
// s在进行拆分二进制的时候,也就对应了此种方法 选择了多少个此种物品作为一个新的物品
// 那与之对应的vw也就需要更新,作为一种新物品单独看待
w[count] = wi * k;
si -= k; // s 分解成2的0到k次 幂(小于s),
k *= 2; // k每次都成2,就是2的倍数
}
//比如10,分成 1 2 4 如果加上8加能够凑出1-15个数,所以超过10,所以我们用10减去前面的数,剩下3
//所以分成 1 2 4 3
//下面这一步就是判断生下来的数是多少
if(si > 0){
count++;
v[count] = vi * si; // 此处的si也就是剩下的c,也当做一个新的物品即可
w[count] = wi * si;
}
}
// 01背包问题解决每种新物品的选择问题
for(int i = 1; i <= count; i++){
// 拆分s之后每种情况都进行遍历,也就意味着每个si都会根据01背包来确定是否进行重新组合
for(int j = m; j >= v[i]; j--){
f[j] = Math.max(f[j], f[j - v[i]] + w[i]);
}
}
System.out.println(f[m]);
}
}
 文章来源地址https://www.toymoban.com/news/detail-722426.html
文章来源地址https://www.toymoban.com/news/detail-722426.html
import java.util.*;
import java.io.*;
/*
// 一共3组,背包容量为5
3 5
//下面是第一组,一共两件物品
2
//第一件物品的体积为1,价值为2
//第二件物品的体积为2,价值为4
1 2
2 4
//第二组
1
3 4
//第三组
1
4 5
*/
public class Main{
static int n,m;
static int N = 110;
// 此处的ij分别代表的是第i组的第j个物品
static int[][] v = new int[N][N];
static int[][] w = new int[N][N];
static int[] s = new int[N];
static int[] f = new int[N];
public static void main(String[] args) throws IOException {
BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
String[] str1 = in.readLine().split(" ");
n = Integer.parseInt(str1[0]);
m = Integer.parseInt(str1[1]);
for(int i = 1; i <= n; i++){
String str2 = in.readLine();
s[i] = Integer.parseInt(str2);
for(int j = 1; j <= s[i];j ++){
String[] str3 = in.readLine().split(" ");
v[i][j]= Integer.parseInt(str3[0]);
w[i][j] = Integer.parseInt(str3[1]);
}
}
for(int i = 1; i <= n; i++){
for(int j = m; j >= 0; j--){
// 因为用到的是f【i-1】【j - v[i][k]】处理,不能对之前的进行更新
for(int k = 1; k <= s[i]; k++){ // 此处存储的是每组里面的物品数量
if(v[i][k] <= j){
f[j] = Math.max(f[j], f[j - v[i][k]] + w[i][k]);
}
}
}
}
System.out.println(f[m]);
}
}
到了这里,关于三十八、动态规划——背包问题( 01 背包 + 完全背包 + 多重背包 + 分组背包 + 优化)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!