排序算法（python）-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序算法（python）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

排序算法

冒泡排序

连续的比较和交换相邻元素实现排序。

依次比较相邻的两个数，每轮之后末尾的数字是确定的。

时间复杂度为 $O(n^2)$ ，空间复杂度为 $O (1)$ ，稳定。

def BUB(nums):
	for i in range(len(nums)):
		count = 0
		for j in range(len(nums)-i-1):
			if nums[j] > nums[j+1]:
				nums[j], nums[j+1] = nums[j+1], nums[j]
				count += 1
		# count是为了记录该轮是否有修改的，若没有修改，则说明当前数组已经满足条件，不需要再进行交换了。
		if count == 0:
			break
	return nums

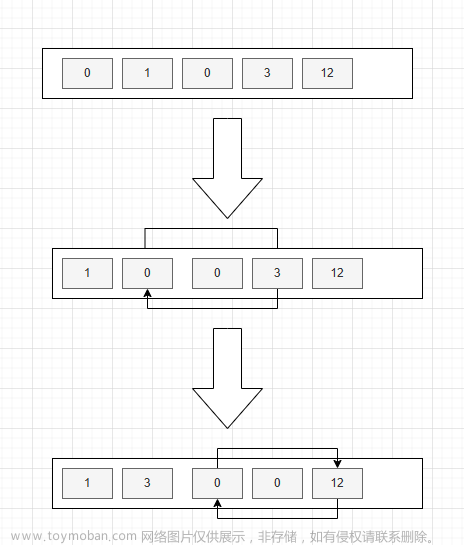
选择排序

从未排序的区间选择最小元素，放在已排序区间的末尾

选择排序是每轮在剩余的元素中，找到最小的元素交换位置。

时间复杂度为 $O(n^2)$ ，空间复杂度为 $O (1)$ ，不稳定。

def selection(nums):
	for i in range(len(nums)-1):
		k = i
		for j in range(i+1, len(nums)):
			if nums[k] > nums[j]:
				k = j
		nums[i], nums[k] = nums[k], nums[i]
	return nums

插入排序

插入排序是默认前面的序列是有序的，然后将后面的每个数字依次与前面有序的序列进行比较

时间复杂度为 $O(n^2)$ ，空间复杂度为 $O (1)$ ，稳定。

def insertSort(nums):
	for i in range(len(nums)-1):
		for j in range(i+1, 0, -1):
			if nums[j] < nums[j-1]:
				nums[j], nums[j-1] = nums[j-1], nums[j]
			else:
				break
	return nums

希尔排序

希尔排序是对插入排序的优化，它选择了一个增量(len(nums)//2)，然后按照这个增量选取等差数列，每轮对每个等差数列进行排序，然后将增量缩小，重复进行排列，直到增量缩小为1。

时间复杂度为 $O(nlog_2^n)$ ，空间复杂度为 $O (1)$ ，稳定。

def xier(nums):
	l = len(nums)
	gap = l//2
	while gap>0:
		for i in range(gap, l):
			temp = nums[i]
			j = i
			# j-gap就相当于等差数列进行排序比较
			while j-gap>0 and temp < nums[j-gap]:
				nums[j] = nums[j-gap]
				j = j-gap
			nums[j]=temp
		gap-=1
	return nums

def xier(nums):
	l = len(nums)
	gap = l // 2
	while gap>0:
		for i in range(l-gap):
			for j in range(i+gap, 0, -gap):
				if nums[j] < nums[j-gap]:
					nums[j], nums[j-gap] = nums[j-gap], nums[j]
				else:
					break
		gap -= 1
	return nums

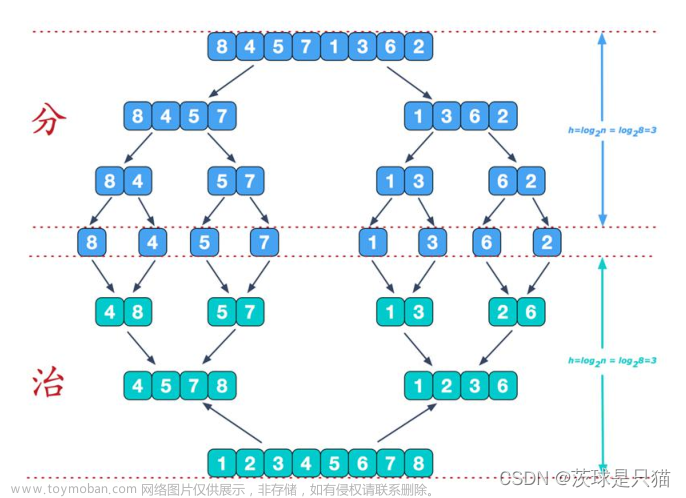
归并排序

合并两个已经排好序的序列以得到结果。是一个递归的过程。

时间复杂度为 $O (n l o g n)$ ，空间复杂度为 $O (n)$ ，稳定。

# 合并两个有序的数组
def merge_two(s1,s2,s):
	i, j = 0, 0
	while (i+j) < len(s):
		# j==len(s2)时说明s2走完了，或者s1没走完并且s1中该位置是最小的
		if j==len(s2) or (i<len(s1) and s1[i] < s2[j]):
			s[i+j] = s1[i]
			i += 1
		else:
			s[i+j] = s2[j]
			j += 1
def merge(s):
	l = len(s)
	if l<2:
		return
	mid = l//2
	s1 = s[0:mid]
	s2 = s[mid:l]
	merge(s1)
	merge(s2)
	merge_two(s1, s2, s)
	# merge_two(merge(s[:mid]), merge(s[mid:l]), s)

快速排序

快速排序需要一个基准元素，以及左右两个指针l,r，首先从右端元素开始与基准元素进行比较，找到比基准元素小的数字，放到左端，然后从左端开始寻找比右端大的元素放到r的位置。一轮之后，基准元素左端都是比基准元素小的，右端都是比基准元素大的。然后再依次遍历基准元素左边和右边的序列。文章来源地址https://www.toymoban.com/news/detail-722462.html

时间复杂度为 $O (n l o g n)$ ，空间复杂度为 $O (n)$ ，不稳定。

def quick_sort(nums, start, end):
	if start >= end:
		return
	pivot = nums[start]
	l, r = start, end
	while l<r:
		while l<r and nums[r] > pivot:
			r-=1
		nums[l] = nums[r]
		while l<r and nums[l] < pivot:
			l+=1
		nums[r] = nums[l]
	nums[l] = pivot
	quick_sort(nums, start, l)
	quick_sort(nums, l+1, end)