倒立摆动态系统的数学建模与分析
最优控制理论是一种数学方法,用于设计和分析控制系统,以使系统的性能最优。它的目标是找到一种控制策略,使得系统在满足一定的约束条件下,能够以最优的方式实现某种目标。
1. 涉及的一些基础知识和方程
牛顿第二定律: F = m ⋅ a F = m \cdot a F=m⋅a
转动定律: W = I ⋅ α W=I \cdot \alpha W=I⋅α
矩阵、微积分、诱导公式、线性代数、拉布拉斯变换、传递函数、空间状态方程
状态方程: x ˙ ( t ) = f ( x ( t ) , u ( t ) ) \dot{x}(t) = f(x(t),u(t)) x˙(t)=f(x(t),u(t))
其中, x ( t ) x(t) x(t)为系统状态向量, u ( t ) u(t) u(t)为控制器输入。
控制方程: u ( t ) = g ( x ( t ) ) u(t) = g(x(t)) u(t)=g(x(t))
其中, g ( x ( t ) ) g(x(t)) g(x(t))为控制器输出,可以是某个线性或非线性函数。
性能指标: J = ∫ 0 ∞ L ( x ( t ) , u ( t ) , t ) d t J = \int_{0}^{\infty} L(x(t), u(t), t) dt J=∫0∞L(x(t),u(t),t)dt
其中, L ( x ( t ) , u ( t ) , t ) L(x(t), u(t), t) L(x(t),u(t),t)为某个关于系统状态、控制器输入和时间的函数,用于评估控制器性能。
求解方法: 动态规划、最优控制、优化等数学方法。
最优控制器设计: 给定某个控制目标和性能指标,可以使用状态反馈控制或输出反馈控制方法设计最优控制器。
状态空间表示: 系统状态、控制器输入和输出可以用向量表示,即
x ( t ) = [ x 1 ( t ) , x 2 ( t ) , . . . , x n ( t ) ] T x(t) = [x_1(t), x_2(t), ..., x_n(t)]^T x(t)=[x1(t),x2(t),...,xn(t)]T
u ( t ) = [ u 1 ( t ) , u 2 ( t ) , . . . , u m ( t ) ] T u(t) = [u_1(t), u_2(t), ..., u_m(t)]^T u(t)=[u1(t),u2(t),...,um(t)]T
其中, n n n和 m m m分别为系统状态和控制器输入的维度。系统状态方程可以写成矩阵形式:
x ˙ ( t ) = A x ( t ) + B u ( t ) \dot{x}(t) = Ax(t) + Bu(t) x˙(t)=Ax(t)+Bu(t)
其中, A A A为系统状态矩阵, B B B为控制矩阵。控制器方程可以表示为:
u ( t ) = K x ( t ) + v ( t ) u(t) = Kx(t) + v(t) u(t)=Kx(t)+v(t)
其中, K K K为反馈矩阵, v ( t ) v(t) v(t)为某个外部干扰。系统输出可以表示为:
y ( t ) = C x ( t ) + D u ( t ) y(t) = Cx(t) + Du(t) y(t)=Cx(t)+Du(t)
其中, C C C和 D D D分别为输出矩阵和直接通道矩阵。文章来源:https://www.toymoban.com/news/detail-722598.html
2. 受力分析与方程建立
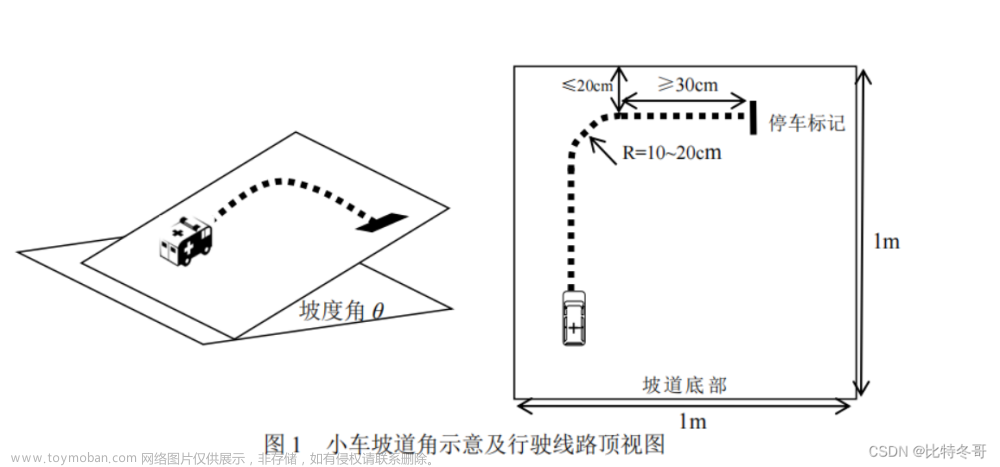
假设小车质量 M (千克) M(千克) M(千克),摆的质量 m (千克) m(千克) m(千克),质量均匀的摆杆的长度 2 l (米) 2l(米) 2l(米),摆的转动惯量为 I (千克 . 米 2 ) I(千克.米^2) I(千克.米2),作用在小车身上的外部控制力 u (牛) u(牛) u(牛),不考虑车轮打滑和小车受到的阻尼力,小车在空间坐标系中的相对位置 z (米) z(米) z(米),摆的角度 θ (度) \theta(度) θ(度),受力分析与方程建立:
对小车水平方向受力分析,根据牛顿第二定律可得: u − N = M ⋅ z ¨ u-N=M \cdot z̈ u−N=M⋅z¨,小车水平方向受力为:
M ⋅ z ¨ + N = u , ( 1 ) M \cdot z̈+N=u,(1) M⋅z¨+N=u,(1) 对摆杆的水平方向受力分析,
N = m ⋅ d 2 d t 2 ( z + l ⋅ s i n θ ) , ( 2 ) N=m \cdot \frac{d^2}{dt^2}( z+l \cdot sin\theta) ,(2) N=m⋅dt2d2(z+l⋅sinθ),(2) 使用诱导公式和微分计算可得到:
N = m ⋅ z ¨ + m ⋅ l ⋅ θ ¨ ⋅ c o s θ − m ⋅ l ⋅ θ ˙ 2 ⋅ s i n θ , ( 3 ) N=m \cdot z̈+m \cdot l \cdot \ddot{\theta} \cdot cos\theta -m \cdot l \cdot \dot{\theta}^2 \cdot sin\theta, (3) N=m⋅z¨+m⋅l⋅θ¨⋅cosθ−m⋅l⋅θ˙2⋅sinθ,(3) 对摆杆的垂直平方向受力分析,
m ⋅ g − P = m ⋅ d 2 d t 2 ( l ⋅ c o s θ ) , ( 4 ) m \cdot g - P=m \cdot \frac{d^2}{dt^2}( l \cdot cos\theta) ,(4) m⋅g−P=m⋅dt2d2文章来源地址https://www.toymoban.com/news/detail-722598.html
到了这里,关于倒立摆系统之PID和LQR控制原理的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!