QR分解
在解最小二乘问题 m i n ∣ ∣ A x − b ∣ ∣ min||Ax-b|| min∣∣Ax−b∣∣时,将其转化成 A T A x = A T b A^{T}Ax=A^{T}b ATAx=ATb之后该问题就是一个求解线性方程组的问题。最简单的求解线性方程组方法是高斯消去,但是有时高斯消去会增大方程的条件数,这时我们可以用正交分解来解决这个问题,即 A x = b → Q R x = b Ax=b \rightarrow QRx=b Ax=b→QRx=b,其中 Q Q Q是正交矩阵( Q T Q = I Q^{T}Q=I QTQ=I), R R R是上三角矩阵。
1.Gram Schmidt正交化
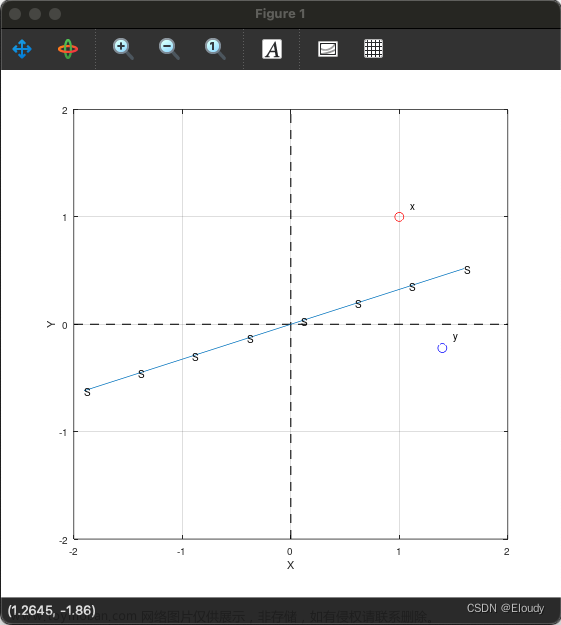
希望将一般向量组 ( a 1 , a 2 , . . . , a m ) (a_{1},a_{2},...,a_{m}) (a1,a2,...,am)转化成一组正交向量 ( b 1 , b 2 , . . . , b m ) (b_{1},b_{2},...,b_{m}) (b1,b2,...,bm)。
- step1 令
b
1
=
a
1
b_{1}=a_{1}
b1=a1,
b
2
=
a
2
−
k
b
1
b_{2}=a_{2}-kb_{1}
b2=a2−kb1,希望
b
1
,
b
2
b_{1},b_{2}
b1,b2正交,即
<
b
1
,
b
2
>
=
0
<b_{1},b_{2}>=0
<b1,b2>=0
→ < b 1 , a 2 − k b 1 > = 0 \rightarrow <b_{1},a_{2}-kb_{1}>=0 →<b1,a2−kb1>=0
→ < b 1 , a 2 > − k < b 1 , b 1 > = 0 \rightarrow<b_{1},a_{2}>-k<b_{1},b_{1}>=0 →<b1,a2>−k<b1,b1>=0
→ k = < b 1 , a 2 > < b 1 , b 1 > \rightarrow k=\frac{<b_{1},a_{2}>}{<b_{1},b_{1}>} →k=<b1,b1><b1,a2>。 - step2 令
b
3
=
a
3
−
k
1
b
1
−
k
2
b
2
b_{3}=a_{3}-k_{1}b_{1}-k_{2}b_{2}
b3=a3−k1b1−k2b2,则希望
<
b
1
,
b
3
>
=
0
,
<
b
2
,
b
3
>
<b_{1},b_{3}>=0,<b_{2},b_{3}>
<b1,b3>=0,<b2,b3>同时成立,即
< b 1 , a 3 − k 1 b 1 − k 2 b 2 > = 0 <b_{1},a_{3}-k_{1}b_{1}-k_{2}b_{2}>=0 <b1,a3−k1b1−k2b2>=0
→ < b 1 , a 3 − k 1 b 1 > = 0 \rightarrow <b_{1},a_{3}-k_{1}b_{1}>=0 →<b1,a3−k1b1>=0
→ k 1 = < b 1 , a 3 > < b 1 , b 1 > \rightarrow k_{1}=\frac{<b_{1},a_{3}>}{<b_{1},b_{1}>} →k1=<b1,b1><b1,a3>,同理可以推出 k 2 = < b 2 , a 3 > < b 2 , b 2 > k_{2}=\frac{<b_{2},a_{3}>}{<b_{2},b_{2}>} k2=<b2,b2><b2,a3>。
施密特正交化的最终形式为
b
m
=
a
m
−
k
1
b
1
−
k
2
b
2
−
.
.
.
−
k
m
−
1
b
m
−
1
b_{m}=a_{m}-k_{1}b_{1}-k_{2}b_{2}-...-k_{m-1}b_{m-1}
bm=am−k1b1−k2b2−...−km−1bm−1,其中,
k
i
=
<
b
i
,
a
m
>
<
b
i
,
b
i
>
k_{i}=\frac{<b_{i},a_{m}>}{<b_{i},b_{i}>}
ki=<bi,bi><bi,am>。令
A
=
[
a
1
,
a
2
,
.
.
.
,
a
n
]
,
B
=
[
b
1
,
b
2
,
.
.
.
,
b
n
]
A=[a_{1},a_{2},...,a_{n}],B=[b_{1},b_{2},...,b_{n}]
A=[a1,a2,...,an],B=[b1,b2,...,bn],则有
A
=
B
T
R
A=B^{T}R
A=BTR,其中
B
B
B是正交矩阵,
R
R
R是上三角矩阵,且
R
=
1
k
k
1
k
1
0
1
k
2
k
2
0
0
1
k
3
0
0
0
1
R=\begin{array}{cccc} 1 & k & k_{1} & k_{1}\\ 0 & 1 & k_{2} & k_{2}\\ 0 & 0 & 1 & k_{3}\\ 0 & 0 & 0 & 1 \end{array}
R=1000k100k1k210k1k2k31
综上,格拉姆-施密特正交化结束。
2.Householder变换
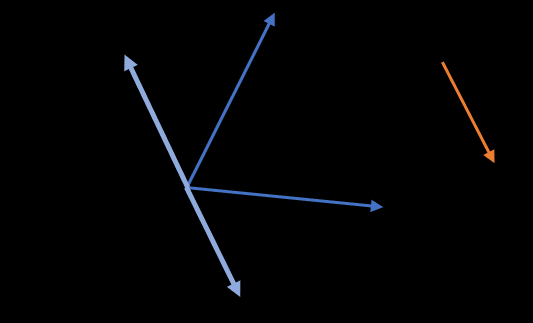
Householder变换是一种镜面反射,即,将一个向量
a
⃗
\vec{a}
a沿
w
⃗
\vec{w}
w的法向量对称到
b
⃗
\vec{b}
b的位置,如下图所示,这个图临时找的,有时间要替换一下。
令
H
=
I
−
2
u
u
T
H=I-2uu^{T}
H=I−2uuT,其中
u
T
u
=
1
u^{T}u=1
uTu=1,则
H
x
=
x
−
2
u
u
T
x
=
x
−
2
(
u
T
x
)
u
Hx=x-2uu^{T}x=x-2(u^{T}x)u
Hx=x−2uuTx=x−2(uTx)u,其中
u
T
x
u^{T}x
uTx是标量,显然
2
(
u
T
x
)
u
2(u^{T}x)u
2(uTx)u与
u
⃗
\vec{u}
u平行且相等,平行在图像中可以看出来,图中虚线和
w
w
w平行,但其实这个相等我没推出来,但是代入一些特殊向量如
w
w
w和
v
,
v
T
w
=
0
v,v^{T}w=0
v,vTw=0两个向量都成立。
在正交分解中,Householder变换主要用来将一般向量 x ⃗ \vec{x} x变换成向量 y ⃗ = ( c , 0 , 0 , . . . , 0 ) \vec{y}=(c,0,0,...,0) y=(c,0,0,...,0),因为该向量是镜面反射,所以只能由 x ⃗ \vec{x} x变成目标向量 y ⃗ = ( ∣ x ⃗ ∣ , 0 , 0 , . . . , 0 ) \vec{y}=(|\vec{x}|,0,0,...,0) y=(∣x∣,0,0,...,0)。而 u ⃗ \vec{u} u一定和 x ⃗ − y ⃗ \vec{x}-\vec{y} x−y平行,同时 u ⃗ \vec{u} u是单位向量,因此 u ⃗ = x ⃗ − y ⃗ ∣ x ⃗ − y ⃗ ∣ \vec{u}=\frac{\vec{x}-\vec{y}}{|\vec{x}-\vec{y}|} u=∣x−y∣x−y,再代入 H = I − 2 u u T H=I-2uu^{T} H=I−2uuT就找到了Householder矩阵 H H H。
下面讲怎么用Householder变换做QR分解。
对于矩阵
A
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
A=\begin{array}{cccc} x & x & x & x\\ x & x & x & x\\ x & x & x & x\\ x & x & x & x \end{array}
A=xxxxxxxxxxxxxxxx使用Householder变换可以找到
H
H
H,使得
H
A
=
x
x
x
x
0
x
x
x
0
x
x
x
0
x
x
x
HA=\begin{array}{cccc} x & x & x & x\\ 0 & x & x & x\\ 0 & x & x & x\\ 0 & x & x & x \end{array}
HA=x000xxxxxxxxxxxx
再用 H 1 ′ = 1 0 0 H 1 H_{1}'=\begin{array}{cccc} 1 & 0 \\ 0 & H_{1}\\ \end{array} H1′=100H1依次对下一列进行Householder变换,就可以得到最终的上三角矩阵。文章来源:https://www.toymoban.com/news/detail-722895.html
3.Givens变换(初等旋转变换)
使用初等旋转矩阵
G
=
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
G=\begin{array}{cccc} cos\theta & -sin\theta \\ sin\theta & cos\theta \\ \end{array}
G=cosθsinθ−sinθcosθ
作用到
x
=
[
x
i
,
x
j
]
T
x=[x_{i},x_{j}]^{T}
x=[xi,xj]T上,有
G
x
=
[
x
i
2
+
x
j
2
,
0
]
T
Gx=[\sqrt{x_{i}^{2}+x_{j}^{2}},0]^{T}
Gx=[xi2+xj2,0]T,从而可以将一个二维向量的某一项变为0,将其用到QR分解中,对于矩阵
A
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
A=\begin{array}{cccc} x & x & x & x\\ x & x & x & x\\ x & x & x & x\\ x & x & x & x \end{array}
A=xxxxxxxxxxxxxxxx
使用Givens变换可以找到矩阵
A
=
1
0
0
0
0
1
0
0
0
0
c
−
s
0
0
s
c
A=\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & c & -s\\ 0 & 0 & s & c \end{array}
A=1000010000cs00−sc使得
G
A
=
x
x
x
x
x
x
x
x
x
x
x
x
0
x
x
x
GA=\begin{array}{cccc} x & x & x & x\\ x & x & x & x\\ x & x & x & x\\ 0 & x & x & x \end{array}
GA=xxx0xxxxxxxxxxxx
一次生成一个0,因此依次进行Givens变换也可以得到最终的上三角矩阵
R
R
R,实现QR分解。文章来源地址https://www.toymoban.com/news/detail-722895.html
到了这里,关于QR分解的三种方法和实现过程的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!