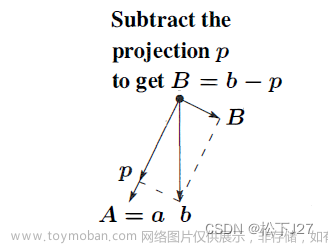
目的: 从矩阵的角度理解高斯消元法, 完成LU分解得到A=LU
1.矩阵乘积的逆矩阵 Inverse of a product

2.矩阵乘积的转置 Transpose of a product

3.转置矩阵的逆矩阵 Inverse of a transpose

4.矩阵的LU分解



U为上三角阵(Upper triangular matrix), L为下三角阵(Lower triangular matrix), 通过分解得到对角阵D(diagonal matrix)

4.1 三阶矩阵不需要换行进行消元的情况则有: (no row exchanges)

设定一组消元矩阵,其中E31为单位阵I,其它两个消元矩阵如下:

row3-5newrow2=row3-5(row2-2row1)=row3-5row2+10 row1
E(left of A) EA=U
4.2 inverses (reverse order)
右侧操作则不会有这种情况发生,运算顺序会发生变化


E(left of U) A=LU
if no row exchanges, multipliers go directly into L 没有多余的交叉项出现是LU分解要优于EA=U这种形式的原因之一
5. How many operations on n×n matrix A? 消元法所需运算量

6. 置换矩阵Permutation Matrix
如果主元的位置出现了0,就需要进行“行交换”。我们可以通过左乘一个置换矩阵(Permutation Matrix)实现“行交换”的操作. 置换矩阵每一行或者每一列只有一个元素是1,其它都是0

为了实现33矩阵的第一行与第二行的交换, 有6个置换矩阵
nxn矩阵存在着n!个置换矩阵文章来源:https://www.toymoban.com/news/detail-724043.html
置换矩阵的逆矩阵
某阶的置换矩阵集合而言,置换矩阵的两两乘积仍在这个集合中,置换矩阵的逆矩阵也在此集合中。置换矩阵的逆矩阵即为它的转置  文章来源地址https://www.toymoban.com/news/detail-724043.html
文章来源地址https://www.toymoban.com/news/detail-724043.html
到了这里,关于04 MIT线性代数-矩阵的LU分解 Factorization into A=LU的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!