[Python中常用的回归模型算法大全：从线性回归到XGBoost]-Toy模板网

这篇具有很好参考价值的文章主要介绍了[Python中常用的回归模型算法大全：从线性回归到XGBoost]。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

概要

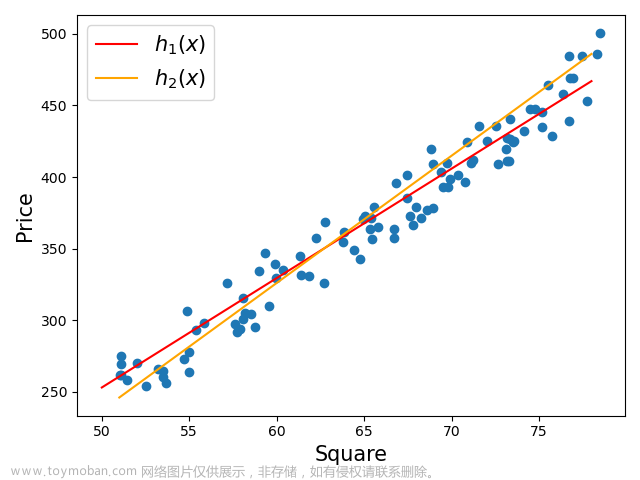
在数据科学和机器学习领域，回归分析是一项关键任务，用于预测连续型变量的数值。除了传统的线性回归模型外，Python提供了丰富多样的回归模型算法，适用于各种复杂的数据关系。本文将深入探讨这些回归模型，并介绍一系列常用的非线性回归方法。我们将涵盖多种模型，包括保序回归、多项式回归、多输出回归、多输出K近邻回归、决策树回归、多输出决策树回归、AdaBoost回归、梯度提升决策树回归、人工神经网络、随机森林回归、多输出随机森林回归以及XGBoost回归。这些模型不仅包括了单一模型，还包括了一些集成学习器，可以有效地处理各种回归问题。通过学习和理解这些模型，我们可以更好地选择和应用适合特定数据集的回归算法，提高预测准确性，实现更精准的数据分析和预测。

保序回归：理论与实践

保序回归，又称为单调回归，是一种强大的数据建模技术，用于处理具有自然排序特性的数据。该技术的核心目标是在拟合的过程中保持预测函数的单调性，即在所有点上保持非递减（或非递减）性质，并且尽可能地靠近观测值。
理论背景

保序回归遵循以下规则：

如果预测输入与训练中的特征值完全匹配，则返回相应标签。
如果一个特征值对应多个预测标签值，返回其中一个，具体选择未指定。
如果预测输入高于或低于所有训练特征值，返回最高或最低特征值对应标签。
如果预测输入落入两个特征值之间，预测结果将是一个分段线性函数，由两个最近特征值的预测值计算得到。

import pandas as pd
import numpy as np
# 假设你的数据保存在一个CSV文件中，可以使用pandas读取数据
dataset = pd.read_csv('your_dataset.csv')
n = len(dataset['Adj Close'])
X = np.array(dataset['Open'].values)
y = dataset['Adj Close'].values
from sklearn.isotonic import IsotonicRegression

ir = IsotonicRegression()
y_ir = ir.fit_transform(X, y)

# 可视化
lines = [[[i, y[i]], [i, y_ir[i]]] for i in range(n)]
lc = LineCollection(lines)
plt.figure(figsize=(15, 6))
plt.plot(X, y, 'r.', markersize=12)
plt.plot(X, y_ir, 'g.-', markersize=12)
plt.gca().add_collection(lc)
plt.legend(('Data', 'Isotonic Fit', 'Linear Fit'))
plt.title("Isotonic Regression")
plt.show()

[Python中常用的回归模型算法大全：从线性回归到XGBoost],# 学习笔记,python深度学习,人工智能,回归,算法,python,opencv,线性回归,目标检测,人工智能

在图中，红色散点代表原始数据点（X-y关系图），绿色线表示保序回归拟合后的数据点（X-y_ir关系图）。这种可视化方式生动展示了保序回归的理论规则。通过这个例子，我们可以更好地理解和应用保序回归，处理那些具有自然排序关系的数据集，提高预测的准确性和可解释性。

多项式回归：探索数据曲线关系

多项式回归是一种非线性回归方法，它允许我们通过引入预测变量的高阶项，更好地拟合曲线关系。与简单线性回归不同，多项式回归能够处理更为复杂的数据模式，因此在描述曲线关系时非常有用。
使用sklearn进行多项式拟合

在这个例子中，我们使用了sklearn库中的PolynomialFeatures进行数据的多项式转换，并使用LinearRegression进行拟合。
数据准备：我们从数据集中提取自变量（特征）X 和因变量（目标）Y。

X = dataset.iloc[:, 0:4].values
Y = dataset.iloc[:, 4].values

多项式转换：使用PolynomialFeatures将数据转换为多项式形式，这里我们选择了3次多项式。

from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=3)
poly_x = poly.fit_transform(X)

拟合模型：使用LinearRegression拟合多项式转换后的数据。

from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(poly_x, Y)

可视化结果：绘制原始数据的X-Y关系散点图，并在同一图中绘制多项式拟合后的曲线。

plt.scatter(X, Y, color='red')
plt.plot(X, regressor.predict(poly.fit_transform(X)), color='blue')
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Polynomial Regression')
plt.show()

展示了两种不同类型的多项式回归方法。第一部分是使用numpy中的polyfit和poly1d进行一元自变量的三阶多项式拟合。第二部分则是使用sklearn中的PolynomialFeatures和Pipeline进行多元自变量的三阶多项式拟合。
一元自变量计算三阶多项式

from scipy import *
f = np.polyfit(X,Y,3)
p = np.poly1d(f)
print(p)

-6.228e-05x + 0.0023x + 0.9766x + 0.05357

多元自变量的多项式

from sklearn.preprocessing import PolynomialFeatures
from sklearn import linear_model
X = np.array(dataset[['Open', 'High', 'Low']].values)
Y = np.array(dataset['Adj Close'].values)

Y = Y.reshape(Y.shape[0], -1)
poly = PolynomialFeatures(degree=3)
X_ = poly.fit_transform(X)
predict_ = poly.fit_transform(Y)
Pipeline形式
from sklearn.pipeline import Pipeline
X = np.array(dataset['Open'].values)
Y = np.array(dataset['Adj Close'].values)
X = X.reshape(X.shape[0], -1)
Y = Y.reshape(Y.shape[0], -1)
Input=[('scale',StandardScaler()),('polynomial', PolynomialFeatures(include_bias=False)),('model',LinearRegression())]
pipe = Pipeline(Input)
pipe.fit(X,Y)
yhat = pipe.predict(X)
yhat[0:4]
array([[3.87445269],
       [3.95484371],
       [4.00508501],
       [4.13570206]])

这部分代码中，使用了Pipeline来实现多元自变量的三阶多项式拟合。首先，对特征进行标准化（StandardScaler），然后使用PolynomialFeatures将特征转换为三阶多项式特征，最后使用LinearRegression进行拟合。Pipeline的使用使得数据预处理和模型拟合过程更加清晰和简单。最终，yhat包含了对数据集进行拟合后的预测结果。

在NumPy中，多项式拟合提供了两个主要的方法：np.poly1d 和 np.polyfit。这些方法使得多项式操作更加方便和直观。

np.poly1d：一维多项式类

np.poly1d 类用于封装多项式上的自然操作，使得多项式可以像常规数学表达式一样使用。它的使用方法如下：

import numpy as np
a = np.array([2, 1, 1])
f = np.poly1d(a)
print(f)

# 输出：2x^2 + 1x + 1

在这个例子中，我们定义了多项式的系数向量 [2, 1, 1]，然后使用 np.poly1d 将其转换为多项式。我们可以像普通函数一样使用这个多项式。

另外，np.poly1d 还允许我们反推多项式，将根转换为多项式：

f = np.poly1d([2, 3, 5], r=True)
print(f)
# 输出：x^3 - 10x^2 + 31x - 30

np.polyfit：最小二乘多项式拟合

np.polyfit 函数用于进行最小二乘多项式拟合，返回拟合多项式的系数。它的使用方法如下：

import numpy as np
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 准备数据
X = dataset['Open'].values
y = dataset['Adj Close'].values

# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25)

# 进行多项式拟合
degree = 3  # 指定多项式的次数
coefficients = np.polyfit(X_train, y_train, degree)

# 创建拟合多项式函数
fitted_polynomial = np.poly1d(coefficients)

# 绘制拟合曲线和数据散点图
plt.figure(figsize=(10, 6))
plt.plot(X_train, y_train, 'bo', label='Training Data')
plt.plot(X_test, y_test, 'r+', label='Testing Data')
plt.plot(X_test, fitted_polynomial(X_test), 'g-', label='Fitted Polynomial')
plt.legend()
plt.xlabel('X')
plt.ylabel('Y')
plt.title('Polynomial Fit using np.polyfit')
plt.show()

在这个例子中，我们使用 np.polyfit 对训练数据进行三阶多项式拟合。然后，我们使用 np.poly1d 创建了拟合多项式函数，最后绘制了拟合曲线（绿色）和训练集（蓝色）以及测试集（红色）的散点图。这样，我们可以直观地看到拟合效果。

NumPy和Scikit-Learn中的多项式回归对比

在机器学习中，多项式回归是一种常用的非线性回归方法。在NumPy和Scikit-Learn中，我们可以使用不同的工具来实现多项式回归。下面我们将比较NumPy和Scikit-Learn中的多项式回归，并通过图形和指标展示它们的效果。

使用NumPy进行多项式回归

import numpy as np
from sklearn.metrics import mean_squared_error as mse
import matplotlib.pyplot as plt

# 一阶多项式拟合
model_one = np.poly1d(np.polyfit(X_train, y_train, 1))

# 二阶多项式拟合
model_two = np.poly1d(np.polyfit(X_train, y_train, 2))

# 三阶多项式拟合
model_three = np.poly1d(np.polyfit(X_train, y_train, 3))

# 绘制拟合曲线和数据散点图
fig, axes = plt.subplots(1, 2, figsize=(14, 5), sharey=True)
labels = ['线性', '二次', '三次']
models = [model_one, model_two, model_three]
train = (X_train, y_train)
test = (X_test, y_test)

for ax, (ftr, tgt) in zip(axes, [train, test]):
    ax.plot(ftr, tgt, 'k+')
    num = 0
    for m, lbl in zip(models, labels):
        ftr = sorted(ftr)
        ax.plot(ftr, m(ftr), '-', label=lbl)
        if ax == axes[1]:
            ax.text(2, 55 - num, f"{lbl}_RMSE: {round(np.sqrt(mse(tgt, m(tgt))), 3)}")
            num += 5

axes[1].set_ylim(-10, 60)
axes[0].set_title("训练集")
axes[1].set_title("测试集")
axes[0].legend(loc='best')

plt.show()

在这段代码中，我们使用NumPy的np.polyfit和np.poly1d进行一阶、二阶和三阶多项式拟合。然后，我们绘制了拟合曲线和训练/测试数据的散点图，并计算了每个模型的均方根误差（RMSE）。

通过比较不同阶数的多项式拟合，我们可以看到三条曲线基本重合，且RMSE相差不大。这说明在这个特定数据集上，不同阶数的多项式回归模型效果相近。
2. 使用Scikit-Learn进行多项式回归

在Scikit-Learn中，可以使用PolynomialFeatures和LinearRegression组合来进行多项式回归：

from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline

# 定义Pipeline
degree = 3
pipeline = Pipeline([
    ('poly_features', PolynomialFeatures(degree=degree)),
    ('lin_reg', LinearRegression())
])

# 拟合模型
pipeline.fit(X_train.reshape(-1, 1), y_train)

# 预测
y_pred = pipeline.predict(X_test.reshape(-1, 1))

# 计算RMSE
rmse = np.sqrt(mse(y_test, y_pred))
print(f"三阶多项式回归的RMSE: {rmse}")

在这段代码中，我们使用了Scikit-Learn的Pipeline，将PolynomialFeatures和LinearRegression组合起来，实现了三阶多项式回归。通过计算RMSE，我们可以得到该模型在测试集上的性能。

总的来说，无论使用NumPy还是Scikit-Learn，多项式回归都是一种强大的工具，可以用来建模非线性关系。选择适当的阶数非常重要，它直接影响了模型的复杂度和泛化性能。在实际应用中，可以通过交叉验证等方法来选择最优的多项式阶数。\

在多项式回归中，多项式的阶数（复杂度）对模型的性能有着重要影响。通过绘制学习曲线，我们可以直观地看出不同阶数多项式模型在训练集和测试集上的表现，从而选择合适的复杂度。

import pandas as pd
import numpy as np
from sklearn.metrics import mean_squared_error as mse
import matplotlib.pyplot as plt

# 初始化结果列表
results = []

# 尝试不同的多项式阶数
for complexity in [1, 2, 3, 4, 5, 6, 7, 8, 9]:
    # 使用多项式拟合训练集
    model = np.poly1d(np.polyfit(X_train, y_train, complexity))
    
    # 计算训练集和测试集的均方根误差
    train_error = np.sqrt(mse(y_train, model(X_train)))
    test_error = np.sqrt(mse(y_test, model(X_test)))
    
    # 将结果加入列表
    results.append((complexity, train_error, test_error))

# 将结果转换为DataFrame
columns = ["复杂度", "训练误差", "测试误差"]
results_df = pd.DataFrame.from_records(results, columns=columns, index="复杂度")

# 绘制学习曲线
results_df.plot(figsize=(10, 6))
plt.xlabel("多项式阶数")
plt.ylabel("均方根误差")
plt.title("多项式回归模型复杂度分析")
plt.show()

在这段代码中，我们尝试了多项式的阶数从1到9。对于每个阶数，我们计算了训练集和测试集的均方根误差，并将结果绘制成学习曲线。通过观察学习曲线，我们可以看到随着多项式阶数的增加，训练误差逐渐降低，但测试误差却开始上升。这表明随着模型复杂度增加，模型在训练集上过度拟合，而在测试集上的泛化性能下降。

多输出回归的示例

多输出回归是一种预测每个样本多个目标值的机器学习任务。在这个任务中，我们希望模型能够为每个样本预测多个属性或目标。例如，对于一个特定地点的天气预测，我们可能需要预测风的方向和大小等多个属性。

在Scikit-Learn中，可以使用MultiOutputRegressor来处理多输出回归任务。这个方法可以将任何回归器包装成多输出回归器。在下面的示例中，我们使用LinearSVR回归器，并将其包装成MultiOutputRegressor：

from sklearn.multioutput import MultiOutputRegressor
from sklearn.svm import LinearSVR

# 准备输入特征和多个目标值
X = dataset.drop(['Adj Close', 'Open'], axis=1)
Y = dataset[['Adj Close', 'Open']]

# 创建LinearSVR回归器
model = LinearSVR()

# 将LinearSVR包装成MultiOutputRegressor
wrapper = MultiOutputRegressor(model)

# 训练多输出回归模型
wrapper.fit(X, Y)

# 准备新的输入数据
data_in = [[23.98, 22.91, 7.00, 7.00, 1.62, 1.62, 4.27, 4.25]]

# 预测多个目标值
yhat = wrapper.predict(data_in)

# 打印预测结果
print(yhat[0])
# 输出: [16.72625136 16.72625136]

# 计算模型的得分（可以根据具体任务选择合适的评估指标）
score = wrapper.score(X, Y)
print("模型得分:", score)

在这个示例中，我们使用MultiOutputRegressor将LinearSVR包装成多输出回归器，并使用给定的输入数据进行预测。然后，我们计算了模型的得分，得分越高代表模型在训练数据上的拟合程度越好。需要注意的是，选择合适的回归器和评估指标对于多输出回归任务非常重要，具体选择应根据任务的特性和数据的分布情况进行。文章来源地址https://www.toymoban.com/news/detail-724328.html

到了这里，关于[Python中常用的回归模型算法大全：从线性回归到XGBoost]的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！