二叉树相关算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了二叉树相关算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1、二叉树基本操作

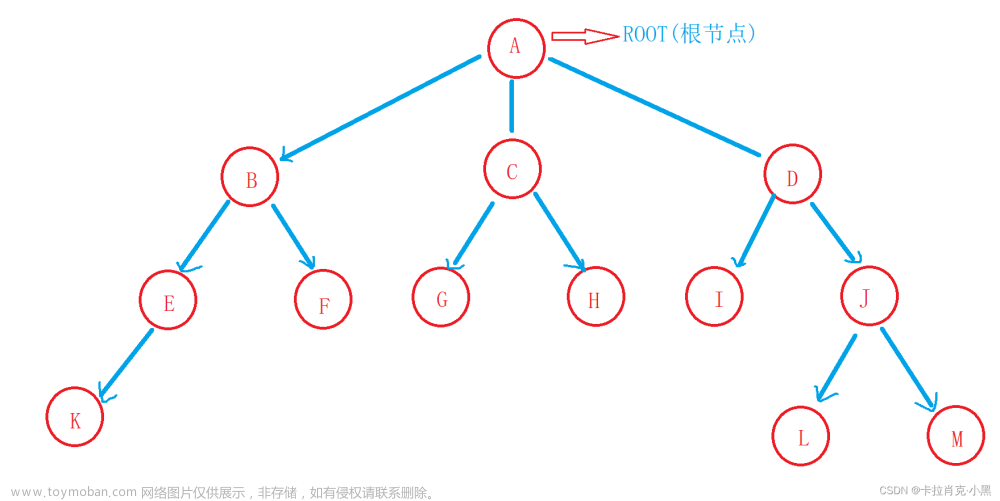
二叉树的定义就不在这里多说了，下面这个图就是一个简单的二叉树：

二叉树相关算法,算法积累,java,开发语言二叉树的三种遍历方式：

前序遍历：头左右，也就是先头后左再右：1245367

    public static void prePrint(BinaryTreeNode root) {
        if (root != null) {
            System.err.print(root.val);
            prePrint(root.left);
            prePrint(root.right);
        }
    }

//非递归方式
    public static void prePrintStack(BinaryTreeNode root) {
        if (root != null) {
            Stack<BinaryTreeNode> queue = new Stack<>();
            queue.add(root);
            while (!queue.isEmpty()) {
                BinaryTreeNode poll = queue.pop();
                System.err.print(poll.val);
                if (poll.right != null) {
                    queue.add(poll.right);
                }
                if (poll.left != null) {
                    queue.add(poll.left);
                }
            }
        }
    }

中序遍历：左头右，也就是先左后头再右：4251637

    public static void midPrint(BinaryTreeNode root) {
        if (root != null) {
            midPrint(root.left);
            System.err.print(root.val);
            midPrint(root.right);
        }
    }

//非递归方式
    public static void midPrintStack(BinaryTreeNode root) {
        if (root != null) {
            Stack<BinaryTreeNode> queue = new Stack<>();
            BinaryTreeNode current = root;
            while (current != null || !queue.isEmpty()) {
                while (current != null) {
                    queue.push(current);
                    current = current.left;
                }
                current = queue.pop();
                System.err.print(current.val);
                current = current.right;
            }
        }
    }

后序遍历：左头右，也就是先左后右再头：4526731

    public static void posPrint(BinaryTreeNode root) {
        if (root != null) {
            posPrint(root.left);
            posPrint(root.right);
            System.err.print(root.val);
        }
    }

//非递归方式
    public void posPrintStack(BinaryTreeNode root) {
        Stack<BinaryTreeNode> stack = new Stack<>();
        stack.push(root);
        BinaryTreeNode prev = null;
        while (!stack.isEmpty()) {
            BinaryTreeNode current = stack.peek();
            if (prev == null || prev.left == current || prev.right == current) {
                if (current.left != null) {
                    stack.push(current.left);
                } else if (current.right != null) {
                    stack.push(current.right);
                }
            } else if (current.left == prev) {
                if (current.right != null) {
                    stack.push(current.right);
                }
            } else {
                System.err.print(current.val);
                stack.pop();
            }
            prev = current;
        }
    }

测试代码：

class BinaryTreeNode {
    int val;
    BinaryTreeNode left;
    BinaryTreeNode right;


    public BinaryTreeNode(int val) {
        this.val = val;
    }

    public BinaryTreeNode(int val, BinaryTreeNode left, BinaryTreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

    public static void main(String[] args) {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        prePrint(one);
        System.err.println();
        midPrint(one);
        System.err.println();
        posPrint(one);
    }

那么我们可以看出来，不论是哪种遍历方式，其在处理左右子节点的时候，逻辑都是一样的，都是要递归处理，不同的只是头结点的输出时机，那么可以优化成下面的代码：

    public static void print(BinaryTreeNode root, int type) {
        switch (type) {
            case 1:
                if (root != null) {
                    System.err.print(root.val);
                    print(root.left, 1);
                    print(root.right, 1);
                }
                break;
            case 2:
                if (root != null) {
                    print(root.left, 2);
                    System.err.print(root.val);
                    print(root.right, 2);
                }
                break;
            case 3:
                if (root != null) {
                    print(root.left, 3);
                    print(root.right, 3);
                    System.err.print(root.val);
                }
                break;
        }
    }

ps：由此可见，递归换做stack通过非递归来实现的时候，如果对顺序由要求，代码要复杂难懂的多

2、两棵树是否结构一样

如下面的图中，只有左上角和右上角两棵树的结构是一样的，才算符合条件：

二叉树相关算法,算法积累,java,开发语言

Java实现判断两棵树是否一样：

    public static boolean isSameTree(BinaryTreeNode node1, BinaryTreeNode node2) {
        if (node1 == null ^ node2 == null) {
            return false;
        }
        if (node1 == null && node2 == null) {
            return true;
        }
        return node1.val == node2.val && isSameTree(node1.left, node2.left) && isSameTree(node1.right, node2.right);
    }

    @Test
    public void testSame() {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        BinaryTreeNode two = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        System.err.println(isSameTree(one, two));
    }

3、镜面树

镜面树有两种情况：

两棵树互为镜面：按照红线对折，可以重叠

单棵树两边互为镜面：二叉树相关算法,算法积累,java,开发语言

代码实现：

    public static boolean isMirror(BinaryTreeNode node1, BinaryTreeNode node2) {
        if (node1 == null ^ node2 == null) {
            return false;
        }
        if (node1 == null && node2 == null) {
            return true;
        }
        return node1.val == node2.val && isMirror(node1.left, node2.right) && isMirror(node1.right, node2.left);
    }

    @Test
    public void testMirror() {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
        BinaryTreeNode two = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
        System.err.println(isMirror(one, two));
    }

4、树的最大深度

二叉树的最大深度其实就是左子树和右子树的最大深度加一，代码实现如下：

    public static int maxDepth(BinaryTreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

    @Test
    public void testMaxDepth() {
        BinaryTreeNode two = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(2, new BinaryTreeNode(5, null, null), new BinaryTreeNode(4, null, null)));
        System.err.println(maxDepth(two));
    }

5、还原二叉树

给定一个二叉树的前序遍历数组和中序遍历数组，两个数组中都没有重复值，根据这两个数组还原二叉树，返回头结点

解题思路：仍然是采用递归的方式，几个重要的解题点：

1、前序遍历的第一个元素一定是树的头结点，比如下面这个最基本的二叉树，前序遍历是1，2，3，中序遍历是2，1，3，所以树的头结点一定是1

2、找出中序遍历数组中头结点所在的位置，假设下标为A，那么在前序遍历数组中，从头结点所在下标加1到A（包括两端），以及在中序序遍历数组中从0到A减1（包括两端）的位置都是左子树的节点

比如下面这棵树的头结点是1，在中序遍历数组中的下标是1，那么2就是左子树，再比如文章最前面的第一棵二叉树，前序遍历1245367和中序遍历4251637，根据第二点我们可以得出前序遍历中的245和中序遍历中的425一定是左子树，右子树的逻辑也类似

二叉树相关算法,算法积累,java,开发语言

代码实现：

 public static BinaryTreeNode buildTree(int[] preorder, int[] inorder) {
        // 构建中序遍历数组中元素与索引的映射关系
        Map<Integer, Integer> inorderMap = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            inorderMap.put(inorder[i], i);
        }
        return buildTreeHelper(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1, inorderMap);
    }

    private static BinaryTreeNode buildTreeHelper(int[] preorder, int preStart, int preEnd,
                                                  int[] inorder, int inStart, int inEnd, Map<Integer, Integer> inorderMap) {
        if (preStart > preEnd || inStart > inEnd) {
            return null;
        }
        int rootVal = preorder[preStart];
        BinaryTreeNode root = new BinaryTreeNode(rootVal);
        if (preStart == preEnd) {//相等的时候说明要么是根节点，要么是到了最后一个节点
            return root;
        }
        int rootIndex = inorderMap.get(rootVal);
        int leftSize = rootIndex - inStart;
        root.left = buildTreeHelper(preorder, preStart + 1, preStart + leftSize,
                inorder, inStart, rootIndex - 1, inorderMap);
        root.right = buildTreeHelper(preorder, preStart + leftSize + 1, preEnd,
                inorder, rootIndex + 1, inEnd, inorderMap);
        return root;
    }

    @Test
    public void testBuildTree() {
        int[] preorder = {1, 2, 4, 5, 3, 6, 7};
        int[] inorder = {4, 2, 5, 1, 6, 3, 7};
//        int[] preorder = {1, 2, 3};
//        int[] inorder = {2, 1, 3};
        BinaryTreeNode root = buildTree(preorder, inorder);
        print(root, 1);
        System.err.println();
        print(root, 2);
        System.err.println();
        print(root, 3);
    }

6、水平收集二叉树

意思是按一层一层的输出二叉树的数据，比如下面的棵树：其输出结果是[[3, 4, 4, 3], [2, ], [1]]

二叉树相关算法,算法积累,java,开发语言

解题思路：

1、用一个队列（栈也可以），存储每一层的节点，那么队列的size就是当前层的节点个数，比如上图的树中，先把1节点放进队列，那么队列的size就是1，然后从队列中把1节点取出来，这个时候队列的size就是0，同时如果取出来的节点有左右子节点，就把左右子节点都放到队列里面去，进行下一轮队列取数

2、第一步是按顺序取出来了每一层的节点，第二部就是把取出来的多个数组倒序输出

代码如下：

public static List<List<Integer>> transverseColectTree(BinaryTreeNode root) {
        List<List<Integer>> result = new LinkedList<>();
        if (null != root) {
            Queue<BinaryTreeNode> queue = new LinkedList();
            queue.add(root);
            while (!queue.isEmpty()) {
                List<Integer> tmpList = new LinkedList<>();
                int size = queue.size();//队列的size就是每一层的节点个数
                for (int i = 0; i < size; i++) {//for循环结束之后，tmpList存储的就是当前层的节点
                    BinaryTreeNode poll = queue.poll();
                    tmpList.add(poll.val);
                    if (poll.left != null) {
                        queue.add(poll.left);
                    }
                    if (poll.right != null) {
                        queue.add(poll.right);
                    }
                }
                result.add(0, tmpList);
            }
        }
        return result;
    }

    @Test
    public void testCransverseColectTree() {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        System.err.println(transverseColectTree(one));
    }

7、判断一棵树是否平衡二叉树

平衡二叉树的概念：对任意一个节点来说，它的左子树的高度和右子树的高度差不超过1

解题思路：我们前面已经右现成的可以求一个节点的最大高度maxDepth函数可以直接用，那么只需要判断当前节点本身是否一个平衡树并且左右子树的高度差不超过1即可

直接上代码：

    //获取root节点左右子树的最大高度
    public static int maxDepth(BinaryTreeNode root) {
        if (root == null) {
            return 0;
        }
        return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

    //判断root节点是否平衡树
    public static boolean isBalancedTree(BinaryTreeNode root) {
        if (root == null) {
            return true;
        }
        return isBalancedTree(root.left) && isBalancedTree(root.right) && Math.abs(maxDepth(root.left) - maxDepth(root.right)) < 1;
    }

    @Test
    public void testBalanced() {
        BinaryTreeNode one = new BinaryTreeNode(1,
                new BinaryTreeNode(2, new BinaryTreeNode(4, null, null), new BinaryTreeNode(5, null, null)),
                new BinaryTreeNode(3, new BinaryTreeNode(6, null, null), new BinaryTreeNode(7, null, null)));
        System.err.println(isBalancedTree(one));
    }

8、判断一棵树是否搜索二叉树

搜索二叉树的特点：

有序性：对于搜索二叉树中的任意节点，其左子树中的所有节点的值都小于该节点的值，而右子树中的所有节点的值都大于该节点的值。这意味着搜索二叉树中的节点是按照一定的顺序排列的。
唯一性：搜索二叉树中不允许有重复的节点。每个节点的值都是唯一的

解题思路：有两种思路，一种是使用中序遍历的方式，因为二叉树的中序遍历是左头右的顺序，所以按照中序遍历出来的数组如果符合严格递增的顺序，那么这颗树就是搜索二叉树，另一种就是根据搜索二叉树的特点来通过递归实现，下面仅展示递归的写法：

    private boolean isValidBST(BinaryTreeNode node, Integer min, Integer max) {
        if (node == null) {
            return true;
        }
//对于任意节点,左子树的最大值必须小于该节点的值且右子树的最小值必须大于该节点的值
        if ((min != null && node.val <= min) || (max != null && node.val >= max)) {
            return false;
        }
        return isValidBST(node.left, min, node.val) && isValidBST(node.right, node.val, max);
    }

    @Test
    public void testBst() {
        BinaryTreeNode one = new BinaryTreeNode(7,
                new BinaryTreeNode(5, new BinaryTreeNode(4, null, null), new BinaryTreeNode(6, null, null)),
                new BinaryTreeNode(8, null, new BinaryTreeNode(9, null, null)));
        System.err.println(isValidBST(one,null,null));
    }

9、判断一棵树是否平衡搜索二叉树

平衡搜索二叉树其实就是前面的第七和第八两个综合起来了，代码就不在这里写了

10、路径和

给定一颗二叉树和一个目标数，从树的根节点到叶子结点为一条完整的路径，如果有任何一条路径上的数字之和等于目标数，就返回true

    public boolean hasPathSum(BinaryTreeNode root, int sum) {
        if (null == root) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }

    @Test
    public void testSumPath() {
        BinaryTreeNode one = new BinaryTreeNode(7,
                new BinaryTreeNode(5, new BinaryTreeNode(4, null, null), new BinaryTreeNode(6, null, null)),
                new BinaryTreeNode(8, new BinaryTreeNode(7, null, null), new BinaryTreeNode(9, null, null)));
        System.err.println(hasPathSum(one, 18));
    }

11、路径和之二

给定一颗二叉树和一个目标数，从树的根节点到叶子结点为一条完整的路径，找出路径上的数字之和等于目标数的所有路径文章来源地址https://www.toymoban.com/news/detail-724373.html

public List<List<Integer>> pathSum(BinaryTreeNode root, int sum) {
        List<List<Integer>> result = new LinkedList<>();
        if (null == root) {
            return result;
        }
        pathSum(root, sum, new LinkedList<Integer>(), result);
        return result;
    }

    public void pathSum(BinaryTreeNode root, int targetSum, List<Integer> curPath, List<List<Integer>> result) {
        curPath.add(root.val);//先把当前节点加到路劲中
        if (root.left == null && root.right == null) {//当前节点是叶子节点
            if (root.val == targetSum) {
                result.add(new LinkedList<>(curPath));
            }
        } else {
            pathSum(root.left, targetSum - root.val, curPath, result);
            pathSum(root.right, targetSum - root.val, curPath, result);
        }
        curPath.remove(curPath.size() - 1);//不论当前节点是否满足，都需要删除还原现场，因为要返回上一级节点，继续算
    }

到了这里，关于二叉树相关算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！