目录
一、稀疏矩阵的生成
1.利用sparse函数建立一般的稀疏矩阵
2.利用特定函数建立稀疏矩阵
二、稀疏矩阵的运算
一、稀疏矩阵的生成
1.利用sparse函数建立一般的稀疏矩阵
稀疏矩阵指令的调用格式：
示例1：输入一个稀疏矩阵
A=sparse([1 2 3 4 5],[2 1 4 6 2],[10 3 -2 -5 1],10,12)运行结果：
此外，sparse函数还可以将一个满矩阵转换成一个稀疏矩阵，相应的调用格式如下：
- S = sparse(X):X为满矩阵。
反之，MATLAB提供了full()函数把稀疏矩阵转换为满矩阵。full()函数的调用格式如下：
- A = full(S):S为稀疏矩阵。
示例2：生成稀疏矩阵A并转换为满矩阵
A=[1 0 0 0;0 5 0 0;2 0 0 7]
B=sparse(A) %转为稀疏矩阵
C=full(B) %转为满矩阵运行结果：
示例3：将普通矩阵转换为稀疏矩阵
A=rand(16,9)>0.95
B=sparse(A) %创建稀疏矩阵
whos运行结果：
示例4：查看稀疏矩阵中非零的信息
A=[0 0 0 1;0 0 8 0;4 0 0 0;0 0 0 0]
B=sparse(A) %创建稀疏矩阵
whos
n1=nnz(B) %查看非零元素个数
n2=nonzeros(B) %非零元素的值
n3=nzmax(B) %查看稀疏矩阵的存储空间
spy(B)
n4=nnz(B)/prod(size(B))运行结果：
注意：
spy()函数对稀疏矩阵中非零元素的分布进行图形化显示：
采用nnz(S)/prod(size(S))计算稀疏矩阵的非零元素密度。
2.利用特定函数建立稀疏矩阵
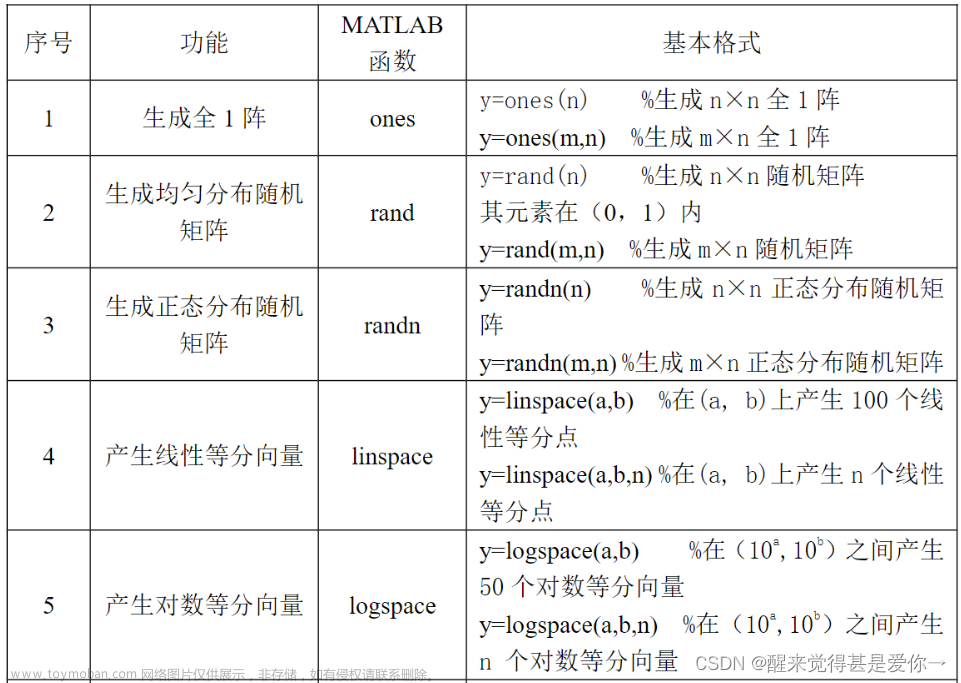
MATLAB提供了一些函数来创建特殊的稀疏矩阵：
示例5：利用speye函数创建单位稀疏矩阵
A=speye(5) %创建5阶单位稀疏矩阵
B= speye (5,6) %创建稀疏矩阵
C=full(A)
D=full(B)运行结果：
示例6：创建非零元素为随机数的对称稀疏矩阵
A=sprandsym(5,0.1) %建立非零元素为随机数的对称稀疏矩阵
B=spones(A) %建立非零元素为1的与矩阵A维数相同的对称稀疏矩阵
C=full(A)
D=full(B)运行结果：每次运行结果不同哦！！！文章来源：https://www.toymoban.com/news/detail-724476.html
文章来源地址https://www.toymoban.com/news/detail-724476.html
二、稀疏矩阵的运算
- 满矩阵的四则运算对稀疏矩阵同样有效，但是返回结果有可能是稀疏矩阵或者满矩阵。
- 对于单个稀疏矩阵的输入，大部分函数输出的结果都是稀疏矩阵，
- 有部分函数输出的结果是满矩阵。对于多个矩阵的输入，如果其中至少有一个矩阵是满矩阵，那么大部分函数的输出结果是满矩阵。
- 对于矩阵的加、减、乘、除运算，只要其中有一个是满矩阵，则输出的结果都是满矩阵。
- 稀疏矩阵的数乘为稀疏矩阵；稀疏矩阵的幂为稀疏矩阵。
到了这里，关于13、稀疏矩阵的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
