简介
基于统计的方法是经典的时间序列预测模型,也是财务时间序列预测的主要方法。他们假设时间序列是由随机冲击的线性集合产生的。一种有代表性的方法是ARMA模型,它是AR和MA模型的组合。它被扩展到非平稳时间序列预测,称为自回归综合移动平均(ARIMA),它结合了差分技术来消除数据中趋势分量的影响,并且由于其巨大的灵活性而成为最受欢迎的线性模型之一。然而,这种方法最初仅限于线性单变量时间序列,并且不能很好地适应多变量设置。为了应对多变量时间序列预测,ARIMA的扩展模型VARMA被提出,该模型通过允许多个进化变量来推广基于单变量ARIMA的模型。
ARIMA模型有三个参数:p、d和q。参数p是模型中滞后观测的数量,也称为滞后阶数。参数d是原始观测值被差分的次数;也称为差异程度。参数q是移动平均窗口的大小,也称为移动平均的阶数。
步骤
- 确定平稳性:ARIMA模型是一种统计模型,用于基于历史数据中存在的自相关来预测未来值。它假设未来趋势将遵循与历史趋势相同的模式,并要求时间序列是固定的。非平稳性会导致预测误差和参数估计不稳定,从而降低预测结果的可靠性。因此,确定时间序列是否稳定非常重要。
- 数据预处理:应用ADF测试来测试原始数据的平稳性。如果测试结果表明数据是非平稳的,则将对数据进行差分,直到达到平稳状态。
- 数据规范化:数据规范化是一种预处理技术,用于将数据调整到一个通用的规模或范围。当处理表现出显著数值幅度的数据时,有必要对数据进行归一化,以促进有效的训练。我在Python中使用了MinMaxScaler函数,并在0和1之间分别转换了每个特性。
- 确定参数:使用AIC准则以及观察自相关图(ACF)和偏自相关图(PACF)。
代码构建
首先导入需要用到的Python包:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller
from statsmodels.tsa.arima.model import ARIMA
from sklearn.preprocessing import MinMaxScaler
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
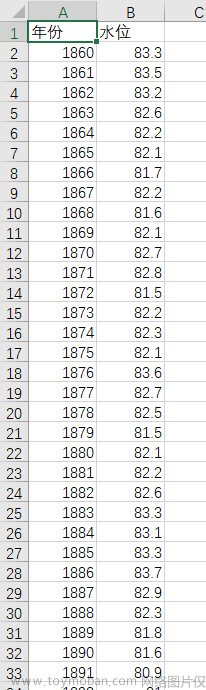
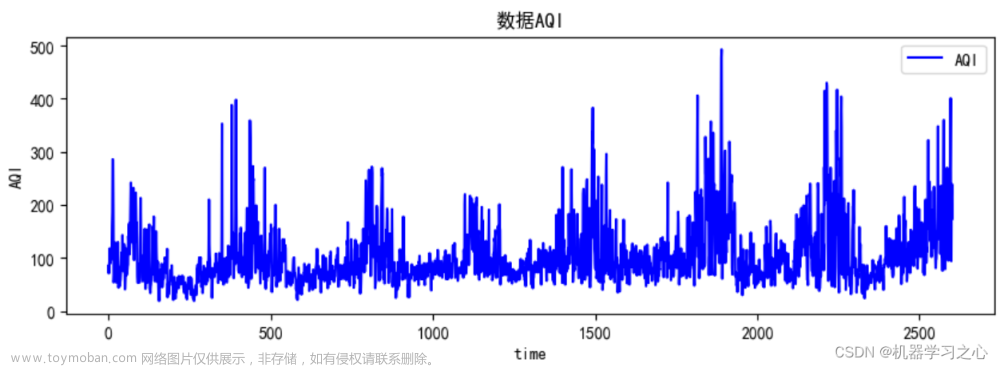
from statsmodels.stats.diagnostic import acorr_ljungbox然后读取.csv文件的时序数据,这里使用了英国的GDP数据
# 1. 读取csv时序数据
data = pd.read_csv('datasets/UK_GDP.csv')[["GDP"]]
data_origin = data.copy()接着使用adf测试判断稳定性
# 2. 使用adf测试数据是否稳定,如果不稳定进行一阶差分,并打印差分前和差分后的数据图。
result = adfuller(data)
print("Test Statistic: %f" % result[0])
print("p-value: %f" % result[1])
print("No. of lags used: %f" % result[2])
print("Number of observations used: %f" % result[3])
print("critical value 1%%: %f" % result[4]["1%"])
print("critical value 5%%: %f" % result[4]["5%"])
print("critical value 10%%: %f" % result[4]["10%"])
if result[1] > 0.05:
diff_data = data.diff().dropna()
plt.figure()
plt.plot(data, label='Original')
plt.plot(diff_data, label='Differenced')
plt.legend()
data = diff_data
else:
plt.figure()
plt.plot(data, label='Original')
plt.legend()然后对处理后的数据进行归一化
# 3. 对处理后数据进行归一化,打印归一化后的图。
scaler = MinMaxScaler()
scaled_data = pd.DataFrame(scaler.fit_transform(data), columns=data.columns, index=data.index)
plt.figure()
plt.plot(scaled_data, label='Scaled')
plt.legend()
然后通过AIC确定参数并打印ACF和PACF图文章来源:https://www.toymoban.com/news/detail-724712.html
# 4. 通过AIC确定ARIMA参数,打印原始数据和差分后数据的自相关系数图和偏自相关系数图,打印确定参数后的残差图。
aic_values = {}
for p in range(6):
for q in range(6):
try:
model = ARIMA(scaled_data, order=(p, 1, q))
result = model.fit()
aic_values[(p, 1, q)] = result.aic
except:
continue
min_aic = min(aic_values, key=aic_values.get)
print("min aci:", min_aic)
model = ARIMA(scaled_data, order=min_aic)
result = model.fit()
fig, axes = plt.subplots(3, 1, figsize=(10, 8))
plot_acf(scaled_data, ax=axes[0])
plot_pacf(scaled_data, ax=axes[1])
residuals = pd.DataFrame(result.resid)
residuals.plot(ax=axes[2])
plt.title('Residuals')
plt.show()最后,计算MAPE和RMSE并打印预测对比图文章来源地址https://www.toymoban.com/news/detail-724712.html
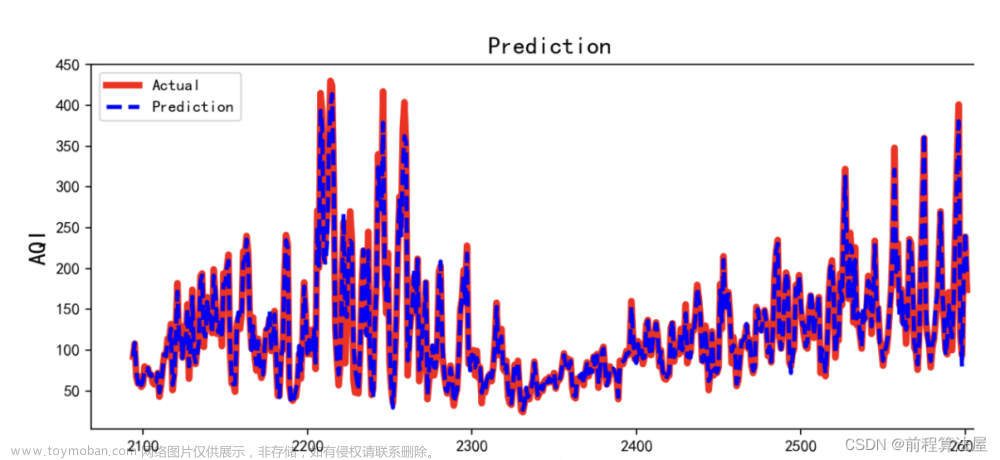
# 5. 使用ARIMA模型进行预测,打印预测值和真实值的对比图,计算模型RMSE和MAPE指标。
train_size = len(scaled_data)-3
train_data, test_data = scaled_data[:train_size], scaled_data[train_size:]
model = ARIMA(train_data, order=min_aic)
result = model.fit()
predictions = result.forecast(steps=len(test_data))
predictions = scaler.inverse_transform(predictions.values.reshape(-1, 1)).flatten()
actual = scaler.inverse_transform(test_data["GDP"].values.reshape(-1, 1)).flatten()
actual = np.array(data[-3:].cumsum() + data_origin.values[127])
predictions = predictions.cumsum() + data_origin.values[127]
plt.figure()
plt.plot(actual, label='Actual')
plt.plot(predictions, label='Predicted')
plt.legend()
plt.show()
rmse = np.sqrt(mean_squared_error(actual, predictions))
mape = mean_absolute_percentage_error(actual, predictions)
print(f"RMSE: {rmse}")
print(f"MAPE: {mape}")
return rmse, mape, actual, predictions到了这里,关于使用Python构造ARIMA模型的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!