矩阵的特征分解
特征值和特征向量的定义
抄来的:奇异值分解
困惑1:特征值和特征向量,和原矩阵是怎样的关系,需要一个栗子进行更具象的认识
困惑2:为什么多个特征向量组合成的矩阵,可以构成矩阵A的特征分解?需要推导
困惑3:为什么要特征向量标准化?
困惑4:标准正交基是什么,为什么满足 W T W = I W^TW=I WTW=I
为什么。。。。
太多why,只能自己来解决吗。。。涕泪横流。。。
先来看看特征值和特征向量
特征值与特征向量的推导
求解特征向量与特征值
A x = λ x Ax=λx Ax=λx,λ是特征值,但特征值可能会有多个,每个特征值都有对应的特征向量
根据
(
A
−
λ
E
)
x
=
0
(A-λE)x=0
(A−λE)x=0,而需要x是非零向量,则要求A-λE的行列式为0,即
∣
A
−
λ
E
∣
=
0
|A-λE|=0
∣A−λE∣=0,就可以求出多个λ值
分别将λ值代入
∣
A
−
λ
E
∣
x
=
0
|A-λE|x=0
∣A−λE∣x=0,就可以求出对应的特征向量x
question:为什么x是非零向量, ∣ A − λ E ∣ = 0 |A-λE|=0 ∣A−λE∣=0的行列式就为0呢?而不是 A − λ E = 0 A-λE=0 A−λE=0向量呢?
still,why?
毫不避讳地说:我大学线性代数是老师给的同情分,60分飘过
但我后来,有自己学习过的,现在也忘个精光了,现在还是重新梳理一遍吧,省的回头海马体又不争气
非零解与行列式值的关系
首先,先从求解矩阵的行列式方法,推导出【非零解与行列式值的关系】
求解行列式,要从【消元法】求解齐次方程组的权重系数w的过程讲起:
- w 1 x 11 + w 2 x 12 + w 3 x 13 = 0 w_1x_{11}+w_2x_{12}+w_3x_{13}=0 w1x11+w2x12+w3x13=0 式子①
- w 1 x 21 + w 2 x 22 + w 3 x 23 = 0 w_1x_{21}+w_2x_{22}+w_3x_{23}=0 w1x21+w2x22+w3x23=0 式子②
- w 1 x 31 + w 2 x 32 + w 3 x 33 = 0 w_1x_{31}+w_2x_{32}+w_3x_{33}=0 w1x31+w2x32+w3x33=0 式子③
通过消元法,求解 w 1 、 w 2 、 w 3 w_1、w_2、w_3 w1、w2、w3:
- 式子①保持: w 1 x 11 + w 2 x 12 + w 3 x 13 = 0 w_1x_{11}+w_2x_{12}+w_3x_{13}=0 w1x11+w2x12+w3x13=0
- 式子②【数乘】【数加】消去
w
1
w_1
w1项
- 数乘: w 1 x 21 x 11 x 21 + w 2 x 22 x 11 x 21 + w 3 x 23 x 11 x 21 = 0 w_1x_{21}\frac{x_{11}}{x_{21}}+w_2x_{22}\frac{x_{11}}{x_{21}}+w_3x_{23}\frac{x_{11}} {x_{21}}=0 w1x21x21x11+w2x22x21x11+w3x23x21x11=0
- 数加①: 式子② -式子①可得 w 1 ∗ 0 + w 2 ( x 22 x 11 x 21 − x 12 ) + w 3 ( x 23 x 11 x 21 − x 13 ) = 0 w_1*0+w_2(x_{22}\frac{x_{11}}{x_{21}}-x_{12})+w_3(x_{23}\frac{x_{11}}{x_{21}}-x_{13})=0 w1∗0+w2(x22x21x11−x12)+w3(x23x21x11−x13)=0
- 即简化为 w 1 ∗ 0 + w 2 b 2 + w 3 b 3 = 0 w_1*0+w_2b_{2}+w_3b_3=0 w1∗0+w2b2+w3b3=0
- 式子③【数乘】【数加】消去
w
1
、
w
2
w_1、w_2
w1、w2项
- 数乘: w 1 x 31 x 11 x 31 + w 2 x 32 x 11 x 31 + w 3 x 33 x 11 x 31 = y 3 x 11 x 31 w_1x_{31}\frac{x_{11}}{x_{31}}+w_2x_{32}\frac{x_{11}}{x_{31}}+w_3x_{33}\frac{x_{11}}{x_{31}}=y_3\frac{x_{11}}{x_{31}} w1x31x31x11+w2x32x31x11+w3x33x31x11=y3x31x11
- 数加①:式子③ -式子①可得 w 1 ∗ 0 + w 2 ( x 32 x 11 x 31 − x 12 ) + w 3 ( x 33 x 11 x 31 − x 13 ) = 0 w_1*0+w_2(x_{32}\frac{x_{11}}{x_{31}}-x_{12})+w_3(x_{33}\frac{x_{11}}{x_{31}}-x_{13})=0 w1∗0+w2(x32x31x11−x12)+w3(x33x31x11−x13)=0
- 数乘再数加消除 w 2 w2 w2,最终可化简为: w 1 ∗ 0 + w 2 ∗ 0 + w 3 c 3 = 0 w_1*0+w_2*0+w_3c_3=0 w1∗0+w2∗0+w3c3=0
通过消元法后:
稍微整理,下列的a\b\c系列都是已知数,求出w
- w 1 a 1 + w 2 a 2 + w 3 a 3 = 0 w_1a_1+w_2a_2+w_3a_3=0 w1a1+w2a2+w3a3=0
- w 1 ∗ 0 + w 2 b 2 + w 3 b 3 = 0 w_1*0+w_2b_{2}+w_3b_3=0 w1∗0+w2b2+w3b3=0
- w 1 ∗ 0 + w 2 ∗ 0 + w 3 c 3 = 0 w_1*0+w_2*0+w_3c_3=0 w1∗0+w2∗0+w3c3=0
这种情况下,方程只有无解,零解和非零解三种情况
将系数写成矩阵
∣
a
1
a
2
a
3
0
b
2
b
3
0
0
c
3
∣
\begin{vmatrix}a_{1}&a_{2}&a_{3}\\0&b_{2}&b_{3}\\0&0&c_{3}\\\end{vmatrix}
a100a2b20a3b3c3
,要使w1、w2、w3三个中有非零解,那就至少需要c3=0-
我觉得我在放屁。。。应该不是这样的,我再衡量衡量
还是偷别的up主教学吧
找个正解的线性代数(三)行列式的来历

好,即使上述关系能体现出,行列式不为零,则有非齐次线性方程组有非零解
但跟求特征根有什么关系呢? ( A − λ E ) x = 0 (A-λE)x=0 (A−λE)x=0
求特征根是求齐次线性方程组的解,但原本求行列式时的方程是非齐次方程组
特征根λ的行列式是:
∣ x 11 − λ x 12 x 13 x 21 x 22 − λ x 23 x 31 x 32 x 33 − λ ∣ \begin{vmatrix}x_{11}-λ&x_{12}&x_{13}\\x_{21}&x_{22}-λ&x_{23}\\x_{31}&x_{32}&x_{33}-λ\\\end{vmatrix} x11−λx21x31x12x22−λx32x13x23x33−λ
然后我又去翻其他的资料,果然。。。前边的分析方向搞错了,只能证明非齐次线性方程组的非零解条件是:行列式≠0
继续论证,齐次线性方程组的非零解条件是:行列式=0,才能说明行列式与特征根的关系


所以,求解非零特征根,是要求齐次线性方程组对应的系数矩阵的秩小于元素个数,也就等同于矩阵的行列式为0。
衍生出新的问题:为什么行列式是这样算的,行列式的本质到底是什么?它的计算有什么代数或几何意义吗?
我觉得,我需要知道它。。。然后去找到知乎一篇文行列式本质
我粗看一遍,感觉这篇文章一定藏着我想要的答案,但首先,我要能看懂它…
我很绝望,行列式的定义是总结归纳出来的吗?
它没有个因果关系吗?
头疼。。。。。
任意矩阵,都可以通过【交换】、【倍乘】、【倍加】的方式,变成上三角矩阵,且不改变行列式的值
B站up主的俗说矩阵,非常好!
穿插理解:行列式
呜呜呜呜呜呜,经过我坚持不懈地在B站摸鱼划水,终于在众说纷纭中,打通了任督二脉
我好像是懂了,懂了n阶行列式的定义,为什么是这样的了!!!!
先摆上二阶行列式的定义:
再摆上三阶行列式的定义:
再摆上n阶行列式的定义:
I don’t know why,how,what
二阶、二阶推导到三阶,我还能理解,但是怎么推出n阶的???
非常头疼,看了很多解释,有些看起来很专业,但我还是不理解
直到回顾到B站的俗说矩阵的行列式按行按列展开
我才有种灵光一闪的开窍!!!哦!!!!
首先,在行列式的二、三阶定义中,可以推导出【数乘】【交换】【数加】三种变换时的行列式变化
- 【行或列数加】:行列式值无改变
- 【行或列数乘】:行列式值乘相同数
- 【行或列相邻交换】:行列式值为相反值

二阶可以由余子式累加得到
通过拆分成三角形式的行列式,可以更好地求的行列式
∣
a
b
x
21
x
22
∣
=
∣
a
0
x
21
x
22
∣
+
∣
0
b
x
21
x
22
∣
\begin{vmatrix}a&b\\x_{21}&x_{22}\\\end{vmatrix}=\begin{vmatrix}a&0\\x_{21}&x_{22}\\\end{vmatrix}+\begin{vmatrix}0&b\\x_{21}&x_{22}\\\end{vmatrix}
ax21bx22
=
ax210x22
+
0x21bx22
下三角无需更换行列,直接求得行列式
∣
a
0
x
21
x
22
∣
=
a
∣
x
22
∣
=
a
x
22
\begin{vmatrix}a&0\\x_{21}&x_{22}\\\end{vmatrix}=a\begin{vmatrix}x_{22}\\\end{vmatrix}=ax_{22}
ax210x22
=a
x22
=ax22
将行列式通过【变换】,变换成下三角后,再求行列式
∣
0
b
x
21
x
22
∣
=
−
∣
b
0
x
22
x
21
∣
=
−
b
∣
x
21
∣
=
−
b
x
21
\begin{vmatrix}0&b\\x_{21}&x_{22}\\\end{vmatrix}=-\begin{vmatrix}b&0\\x_{22}&x_{21}\\\end{vmatrix}=-b\begin{vmatrix}x_{21}\\\end{vmatrix}=-bx_{21}
0x21bx22
=−
bx220x21
=−b
x21
=−bx21
相邻变换,行列式值会变为相反值,因此变换过程有负号产生
三阶也是如此,但三阶是可以由二阶推导来的
∣
x
11
x
12
x
13
x
21
x
22
x
23
x
31
x
32
x
33
∣
=
∣
x
11
0
0
x
21
x
22
x
23
x
31
x
32
x
33
∣
+
∣
0
x
12
0
x
21
x
22
x
23
x
31
x
32
x
33
∣
+
∣
0
0
x
13
x
21
x
22
x
23
x
31
x
32
x
33
∣
\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=\begin{vmatrix}x_{11}&0&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} +\begin{vmatrix}0&x_{12}&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}+\begin{vmatrix}0&0&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}
x11x21x31x12x22x32x13x23x33
=
x11x21x310x22x320x23x33
+
0x21x31x12x22x320x23x33
+
0x21x310x22x32x13x23x33
第一个直接构成下三角
- ∣ x 11 0 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = x 11 ∣ x 22 x 23 x 32 x 33 ∣ = x 11 ∣ x 22 0 x 32 x 33 ∣ + x 11 ∣ 0 x 23 x 32 x 33 ∣ \begin{vmatrix}x_{11}&0&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&x_{23}\\x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}+x_{11}\begin{vmatrix}0&x_{23}\\x_{32}&x_{33}\\\end{vmatrix} x11x21x310x22x320x23x33 =x11 x22x32x23x33 =x11 x22x320x33 +x11 0x32x23x33
- x 11 ∣ x 22 0 x 32 x 33 ∣ + x 11 ∣ 0 x 23 x 32 x 33 ∣ = x 11 ∣ x 22 0 x 32 x 33 ∣ − x 11 ∣ x 23 0 x 33 x 32 ∣ x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}+x_{11}\begin{vmatrix}0&x_{23}\\x_{32}&x_{33}\\\end{vmatrix}=x_{11}\begin{vmatrix}x_{22}&0\\x_{32}&x_{33}\\\end{vmatrix}-x_{11}\begin{vmatrix}x_{23}&0\\x_{33}&x_{32}\\\end{vmatrix} x11 x22x320x33 +x11 0x32x23x33 =x11 x22x320x33 −x11 x23x330x32
- 最终得到: x 11 ∗ x 22 x 33 − x 11 x 23 x 32 x_{11}*x_{22}x_{33}-x_{11}x_{23}x_{32} x11∗x22x33−x11x23x32
第二个需要变换1次,才成为下三角
- ∣ 0 x 12 0 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = − ∣ x 12 0 0 x 22 x 21 x 23 x 32 x 31 x 33 ∣ = − x 12 ∣ x 21 x 23 x 31 x 33 ∣ \begin{vmatrix}0&x_{12}&0\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=-\begin{vmatrix}x_{12}&0&0\\x_{22}&x_{21}&x_{23}\\x_{32}&x_{31}&x_{33}\\\end{vmatrix}=-x_{12}\begin{vmatrix}x_{21}&x_{23}\\x_{31}&x_{33}\\\end{vmatrix} 0x21x31x12x22x320x23x33 =− x12x22x320x21x310x23x33 =−x12 x21x31x23x33
- − x 12 ∣ x 21 x 23 x 31 x 33 ∣ = − x 12 ( ∣ x 21 0 x 31 x 33 ∣ + ∣ 0 x 23 x 31 x 33 ∣ ) = − x 12 ( ∣ x 21 0 x 31 x 33 ∣ − ∣ x 23 0 x 33 x 31 ∣ ) = − x 12 ∗ ( x 21 ∗ ∣ x 33 ∣ − x 23 ∗ ∣ x 31 ∣ ) = − x 12 ∗ x 21 ∗ x 33 + x 12 ∗ x 23 ∗ x 31 -x_{12}\begin{vmatrix}x_{21}&x_{23}\\x_{31}&x_{33}\\\end{vmatrix}= -x_{12}(\begin{vmatrix}x_{21}&0\\x_{31}&x_{33}\\\end{vmatrix}+\begin{vmatrix}0&x_{23}\\x_{31}&x_{33}\\\end{vmatrix}) =-x_{12}(\begin{vmatrix}x_{21}&0\\x_{31}&x_{33}\\\end{vmatrix}-\begin{vmatrix}x_{23}&0\\x_{33}&x_{31}\\\end{vmatrix}) =-x_{12}*(x_{21}*\begin{vmatrix}x_{33}\\\end{vmatrix}-x_{23}*\begin{vmatrix}x_{31}\\\end{vmatrix})=-x_{12}*x_{21}*x_{33}+x_{12}*x_{23}*x_{31} −x12 x21x31x23x33 =−x12( x21x310x33 + 0x31x23x33 )=−x12( x21x310x33 − x23x330x31 )=−x12∗(x21∗ x33 −x23∗ x31 )=−x12∗x21∗x33+x12∗x23∗x31
第三个需要变换2次,才成为下三角
- ∣ 0 0 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = − ∣ 0 x 13 0 x 21 x 23 x 22 x 31 x 33 x 32 ∣ = ∣ x 13 0 0 x 23 x 21 x 22 x 33 x 31 x 32 ∣ = x 13 ∣ x 21 x 22 x 31 x 32 ∣ \begin{vmatrix}0&0&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix} =-\begin{vmatrix}0&x_{13}&0\\x_{21}&x_{23}&x_{22}\\x_{31}&x_{33}&x_{32}\\\end{vmatrix} =\begin{vmatrix}x_{13}&0&0\\x_{23}&x_{21}&x_{22}\\x_{33}&x_{31}&x_{32}\\\end{vmatrix} =x_{13}\begin{vmatrix}x_{21}&x_{22}\\x_{31}&x_{32}\\\end{vmatrix} 0x21x310x22x32x13x23x33 =− 0x21x31x13x23x330x22x32 = x13x23x330x21x310x22x32 =x13 x21x31x22x32
- 同理可推导得: x 13 ∗ x 21 ∗ x 32 − x 13 ∗ x 22 ∗ x 32 x_{13}*x_{21}*x_{32}-x_{13}*x_{22}*x_{32} x13∗x21∗x32−x13∗x22∗x32
为什么要变换的这么详细呢?因为这个过程,恰好展现了n阶行列式的定义!
首先,每一次的变换,都是先把首行中的元素,逐一变换到左上角,这个变换的过程主要与列有关
如果首行元素在奇数列(如第3列),则变换到左上角时,行列式值是不变号的
如果首行元素在偶数列(如第2列),则变换到左上角时,行列式值会变成负号

但除了首行元素的列问题,还有次行元素的列问题
因此,我脑子不够用了,但好在世界上有很多优秀的阿婆主,能讲清楚一些
n阶特征公式解释

具体的,还是看up主的分析会比较有领悟
当然,可能我只是哦!但实际还不是很清晰,但。。。不想特别去深究行列式的定义,大概理解就好
我。。。又快要忘记前边思考的是什么问题了
已理解:行列式是什么,行列式和非零解的关系,可知道当行列式不为零时,求解特征值时,特征值也是非零解
特征值和特征向量的推导
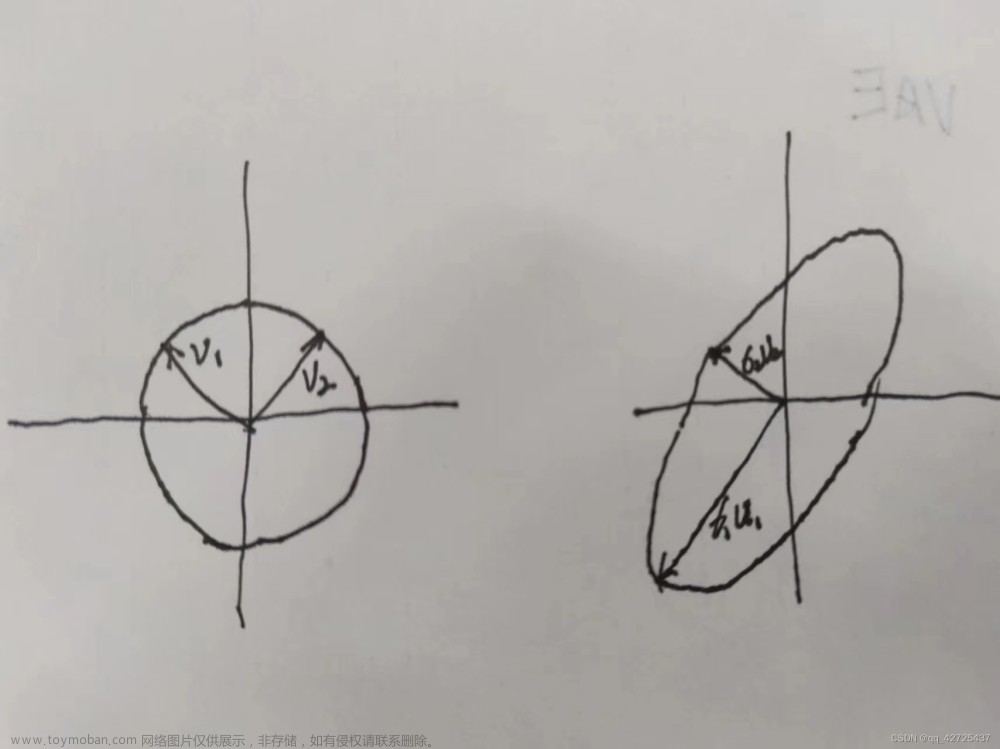
如果从坐标系固定,矩阵向量变换的角度看,矩阵A与向量x相乘 A x Ax Ax,通常是对向量x进行【旋转】+【伸缩】的变换,这个变换过程中,并伴随有【升降维】的作用。
如果从矩阵向量固定,坐标系变换的角度看,矩阵A与向量x相乘 A x Ax Ax,则表示向量x是在A坐标系下,(相当于声明:x是火星A上的人)
而矩阵与特征向量、特征值的关系 A x = λ x Ax=λx Ax=λx,右侧的 λ x λx λx没有矩阵相乘,则表示标准正交基坐标系 I I I下的向量x,只不过这个向量x中每个值都乘以λ倍
而 A x = λ x Ax=λx Ax=λx,则表示,在A坐标系下的特征向量x,实际等同于标准正交基坐标系 I I I里的向量x伸缩λ倍,相当于当坐标系A旋转伸缩变换成标准正交基坐标系 I I I后,向量x的方向没有发生旋转,只是进行了伸缩变换。
向量x,正是特征向量,而特征值λ相当于向量x伸缩的倍数
例如A有一个特征向量
x
1
x_1
x1及对应特征值
λ
1
λ_1
λ1,则
A
x
1
=
λ
1
x
1
Ax_1=λ_1x_1
Ax1=λ1x1
∣
a
11
x
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
∣
x
11
x
21
x
31
∣
=
λ
1
∣
x
11
x
21
x
31
∣
\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}\\x_{21}\\x_{31}\\\end{vmatrix}=λ_1\begin{vmatrix}x_{11}\\x_{21}\\x_{31}\\\end{vmatrix}
a11a21a31x12a22a32a13a23a33
x11x21x31
=λ1
x11x21x31
再例如A的第2 个特征向量
x
2
x_2
x2及对应特征值
λ
2
λ_2
λ2,则
A
x
2
=
λ
2
x
2
Ax_2=λ_2x_2
Ax2=λ2x2
∣
a
11
x
12
a
13
a
21
a
22
a
23
a
31
a
32
a
33
∣
∣
x
12
x
22
x
32
∣
=
λ
1
∣
x
12
x
22
x
32
∣
\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{12}\\x_{22}\\x_{32}\\\end{vmatrix}=λ_1\begin{vmatrix}x_{12}\\x_{22}\\x_{32}\\\end{vmatrix}
a11a21a31x12a22a32a13a23a33
x12x22x32
=λ1
x12x22x32
将A的所有特征向量x组成矩阵W,则有
W
=
∣
x
11
x
12
x
13
x
21
x
22
x
23
x
31
x
32
x
33
∣
W=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}
W=
x11x21x31x12x22x32x13x23x33
要让
λ
1
、
λ
2
、
λ
3
λ_1、λ_2、λ_3
λ1、λ2、λ3对应乘以到W中,则需要将λ形成对角矩阵
Σ
=
∣
λ
1
0
0
0
λ
2
0
0
0
λ
3
∣
Σ=\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix}
Σ=
λ1000λ2000λ3
则
W
Σ
=
∣
λ
1
x
11
λ
2
x
12
λ
3
x
13
λ
1
x
21
λ
2
x
22
λ
3
x
23
λ
1
x
31
λ
2
x
32
λ
3
x
33
∣
WΣ=\begin{vmatrix}λ_1x_{11}&λ_2x_{12}&λ_3x_{13}\\λ_1x_{21}&λ_2x_{22}&λ_3x_{23}\\λ_1x_{31}&λ_2x_{32}&λ_3x_{33}\\\end{vmatrix}
WΣ=
λ1x11λ1x21λ1x31λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33
而 A W = ∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ = W Σ = ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ ∣ λ 1 0 0 0 λ 2 0 0 0 λ 3 ∣ AW=\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}=WΣ=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix} AW= a11a21a31x12a22a32a13a23a33 x11x21x31x12x22x32x13x23x33 =WΣ= x11x21x31x12x22x32x13x23x33 λ1000λ2000λ3
A W W − 1 = W Σ W − 1 AWW^{-1}=WΣW^{-1} AWW−1=WΣW−1,因此就有 A = W Σ W − 1 A=WΣW^{-1} A=WΣW−1
这就是矩阵特征分解的推导
但是,当我有一天深夜,回头看这段的时候,内心依然有个大猩猩捶胸顿足:这里推导出的 A = W Σ W − 1 A=WΣW^{-1} A=WΣW−1,是逆矩阵。而下边的矩阵特征分解 A = W Σ W T A = WΣW^T A=WΣWT,是转置矩阵。
怎么来的?
这就要明确,W本身是正交矩阵,也就是W里的每个向量都是相互垂直(内积为0)且线性无关的。
正交矩阵有个性质:正交矩阵的转置矩阵,等于它的逆矩阵,即 W T = W − 1 W^T=W^{-1} WT=W−1
why?简单论证一下
正交矩阵,意味着矩阵内的任意两个不同向量都是相互垂直(内积为0)且线性无关的。
这意味着: W Σ W T = I WΣW^{T}=I WΣWT=I(不同向量的点乘为0,相同向量的点乘为1,因此形成了单位正交基矩阵I)
而逆矩阵本身的定义就是 W Σ W − 1 = I WΣW^{-1}=I WΣW−1=I
因此,正交矩阵的转置=正交矩阵的逆矩阵
之前一直有个潜意识的误会,以为线性无关的向量组成的矩阵,就是正交矩阵
实际是不正确的
从几何的角度来看:线性无关指的是不共线,正交指的是相互垂直
相互垂直,本身就是不共线,因此,可以说正交矩阵里的任意不同向量,是线性无关的
但向量不共线,并不一定是垂直的,因此线性无关向量组不一定是正交矩阵
两个向量线性相关:表示向量共线,意味着一个向量,可以被另外一个向量表示,这个表示可以用一个伸缩量表示如:A = 5B,向量A和向量B共线。
而线性无关、线性相关,在代数角度来看,指的是一个方程,是否可以由其他方程或其他方程组来表示
如
- a 1 x 1 + b 1 x 2 + c 1 x 3 = 0 a_1x_1 + b_{1}x_2+c_{1}x_3=0 a1x1+b1x2+c1x3=0,方程①
- 0 + b 2 x 2 + c 2 x 3 = 0 0+b_2x_2+c_2x_3=0 0+b2x2+c2x3=0,方程②
- 0 + 0 + c 3 x 3 = 0 0+0+c_3x_3=0 0+0+c3x3=0,方程③
可以看到,上述的方程①②③,均无法通过其他方程来表示,因此这三个方程的系数向量,两两之间都是线性无关的,且方程组本身只有零解
再比如,以下线性相关的栗子🌰
- a 1 x 1 + b 1 x 2 + c 1 x 3 = 0 a_1x_1 + b_{1}x_2+c_{1}x_3=0 a1x1+b1x2+c1x3=0,方程①
- 0 + b 2 x 2 + c 2 x 3 = 0 0+b_2x_2+c_2x_3=0 0+b2x2+c2x3=0,方程②
- 3 a 1 x 1 + ( 3 b 1 + b 2 ) x 2 + ( 3 c 1 + c 2 ) x 3 = 0 3a_1x_1 + (3b_{1}+b_2)x_2+(3c_{1}+c_2)x_3=0 3a1x1+(3b1+b2)x2+(3c1+c2)x3=0,方程③
- 可以看到,上述的方程③,可以由方程①②表示,因此方程③和方程①②之间,是线性相关的
方程组可以简化为以下
- a 1 x 1 + b 1 x 2 + c 1 x 3 = 0 a_1x_1 + b_{1}x_2+c_{1}x_3=0 a1x1+b1x2+c1x3=0,方程①
- 0 + b 2 x 2 + c 2 x 3 = 0 0+b_2x_2+c_2x_3=0 0+b2x2+c2x3=0,方程②
- 0 x 1 + 0 x 2 + 0 x 3 = 0 0x_1 + 0x_2+0x_3=0 0x1+0x2+0x3=0,方程③
方程组本身有非零解
区别了正交和线性无关的关系后,我们知道,W必须是正交矩阵,才有 W T = W − 1 W^T=W^{-1} WT=W−1,进而得到特征值分解公式 A = W Σ W T A = WΣW^T A=WΣWT
我们知道,W是A的特征向量,但A的特征向量组凭什么是正交矩阵?
哭了卧槽。。。。写完的推导。。。。还没来得及更新,就自动没了
心累
总之就是有两个性质,才能证明W是A的正交特征向量组成的矩阵。
性质①:普通方阵的不同特征值,对应的特征向量之间,是线性无关的
性质②:实对称矩阵的不同特征值,对应的特征向量之间,是正交的(内积为0)
简单说说性质①的理解:因为从几何角度看,原坐标系变换为标准正交基坐标系后,如果一个向量的方向没有改变,只是伸缩了λ倍,则称该向量为特征向量,特征值为对应的λ
而如果特征值不同,说明特征向量必然是不同方向的
而代数证明,看大神不同特征值的特征向量线性无关证明
这里,仅给出性质②的推导吧。。。因为心碎了
实对称矩阵的特征值、特征向量均是实数
实对称矩阵的不同特征值,对应的特征向量是相互正交的。
因此,一个实对称矩阵的特征值分解即可推导完成:
A是实对称矩阵,W是A的正交特征向量组(正交矩阵),则有,
W
−
1
=
W
T
,
可推出
A
=
W
Σ
W
T
W^{-1}=W^T,可推出A = WΣW^T
W−1=WT,可推出A=WΣWT
矩阵特征分解的意义
矩阵(方阵),可以由它的所有特征向量和特征值来表示,
例如A是mxm的方阵,它所有的特征向量为mxm的方阵W,对应的特征值矩阵为mxm的对角矩阵Σ
则 A = W Σ W T A = WΣW^T A=WΣWT
特征分解后,可以选择删除一些不重要的特征,对方阵A进行降维。
那怎么知道哪些特征是不重要的呢?
这里的特征,其实指的就是特征向量和特征值,主要看特征值。
如果特征值相对而言特别特别小,接近于0,则这个特征向量对原方阵A的影响相应比较小。
A = ∣ a 11 x 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ∣ = ∣ x 11 x 12 x 13 x 21 x 22 x 23 x 31 x 32 x 33 ∣ ∣ λ 1 0 0 0 λ 2 0 0 0 λ 3 ∣ ∣ x 11 x 21 x 31 x 12 x 22 x 32 x 13 x 23 x 33 ∣ A=\begin{vmatrix}a_{11}&x_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\\\end{vmatrix}=\begin{vmatrix}x_{11}&x_{12}&x_{13}\\x_{21}&x_{22}&x_{23}\\x_{31}&x_{32}&x_{33}\\\end{vmatrix}\begin{vmatrix}λ_1&0&0\\0&λ_2&0\\0&0&λ_3\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{21}&x_{31}\\x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix} A= a11a21a31x12a22a32a13a23a33 = x11x21x31x12x22x32x13x23x33 λ1000λ2000λ3 x11x12x13x21x22x23x31x32x33
A = ∣ λ 1 x 11 λ 2 x 12 λ 3 x 13 λ 1 x 21 λ 2 x 22 λ 3 x 23 λ 1 x 31 λ 2 x 32 λ 3 x 33 ∣ ∣ x 11 x 21 x 31 x 12 x 22 x 32 x 13 x 23 x 33 ∣ A=\begin{vmatrix}λ_1x_{11}&λ_2x_{12}&λ_3x_{13}\\λ_1x_{21}&λ_2x_{22}&λ_3x_{23}\\λ_1x_{31}&λ_2x_{32}&λ_3x_{33}\\\end{vmatrix}\begin{vmatrix}x_{11}&x_{21}&x_{31}\\x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix} A= λ1x11λ1x21λ1x31λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33 x11x12x13x21x22x23x31x32x33
A = ∣ λ 1 x 11 2 + λ 2 x 12 2 + λ 3 x 13 2 λ 1 x 11 x 21 + λ 2 x 12 x 22 + λ 3 x 13 x 23 λ 1 x 11 x 31 + λ 2 x 12 x 32 + λ 3 x 13 x 33 λ 1 x 21 x 11 + λ 2 x 22 x 12 + λ 3 x 23 x 13 λ 1 x 21 x 21 + λ 2 x 22 x 22 + λ 3 x 23 x 23 λ 1 x 21 x 31 + λ 2 x 22 x 32 + λ 3 x 32 x 33 λ 1 x 31 x 11 + λ 2 x 32 x 12 + λ 3 x 33 x 13 λ 1 x 31 x 21 + λ 2 x 32 x 22 + λ 3 x 33 x 23 λ 1 x 31 x 31 + λ 2 x 32 x 32 + λ 3 x 33 x 33 ∣ A=\begin{vmatrix} λ_1x^2_{11}+λ_2x^2_{12}+λ_3x^2_{13} &λ_1x_{11}x_{21}+λ_2x_{12}x_{22}+λ_3x_{13}x_{23} &λ_1x_{11}x_{31}+λ_2x_{12}x_{32}+λ_3x_{13}x_{33}\\ λ_1x_{21}x_{11}+λ_2x_{22}x_{12}+λ_3x_{23}x_{13} &λ_1x_{21}x_{21}+λ_2x_{22}x_{22}+λ_3x_{23}x_{23} &λ_1x_{21}x_{31}+λ_2x_{22}x_{32}+λ_3x_{32}x_{33}\\ λ_1x_{31}x_{11}+λ_2x_{32}x_{12}+λ_3x_{33}x_{13} &λ_1x_{31}x_{21}+λ_2x_{32}x_{22}+λ_3x_{33}x_{23} &λ_1x_{31}x_{31}+λ_2x_{32}x_{32}+λ_3x_{33}x_{33}\\\end{vmatrix} A= λ1x112+λ2x122+λ3x132λ1x21x11+λ2x22x12+λ3x23x13λ1x31x11+λ2x32x12+λ3x33x13λ1x11x21+λ2x12x22+λ3x13x23λ1x21x21+λ2x22x22+λ3x23x23λ1x31x21+λ2x32x22+λ3x33x23λ1x11x31+λ2x12x32+λ3x13x33λ1x21x31+λ2x22x32+λ3x32x33λ1x31x31+λ2x32x32+λ3x33x33
如果将特征值非常小的特征值和对应的特征向量去掉,如删掉λ1和x2,则有
A
=
∣
λ
2
x
12
λ
3
x
13
λ
2
x
22
λ
3
x
23
λ
2
x
32
λ
3
x
33
∣
∣
x
12
x
22
x
32
x
13
x
23
x
33
∣
A = \begin{vmatrix}λ_2x_{12}&λ_3x_{13}\\λ_2x_{22}&λ_3x_{23}\\λ_2x_{32}&λ_3x_{33}\\\end{vmatrix}\begin{vmatrix}x_{12}&x_{22}&x_{32}\\x_{13}&x_{23}&x_{33}\\\end{vmatrix}
A=
λ2x12λ2x22λ2x32λ3x13λ3x23λ3x33
x12x13x22x23x32x33

这样还原出来的A,就不是完完全全的A矩阵了,但相对而言,如果λ1比较小,那么还原出来的矩阵与A矩阵差别也不会太大
奇异值分解SVD
SVD数学推导(简单易懂)
看过一个推导的非常详实的知乎大神:奇异值分解(SVD)
看过理解,不代表真的理解,自己去推导一下吧,搞不好会有一些新的认识
A是mxn的矩阵,U是mxm的方阵,V是nxn的方阵,∑是一个mxn的矩阵,且只有对角线上的元素为非零元素。
那么A、U、V、∑之间有什么关系,才能形成奇异值分解 A = U Σ V T A=UΣV^T A=UΣVT的关系呢?
首先,U是 A A T AA^T AAT方阵的特征向量,特征值为 λ u λ_u λu: A A T U = λ u U AA^TU=λ_uU AATU=λuU
其次,V是 A T A A^TA ATA方阵的特征向量,特征值为 λ v λ_v λv: A T A V = λ v V A^TAV=λ_vV ATAV=λvV
要知道,不同特征值对应的特征向量是线性无关的,因此,它的转置乘以它本身 V T V = U T U = E V^TV=U^TU=E VTV=UTU=E
进而,可以求出奇异矩阵∑, A = U Σ V T → A V = U Σ V T V = U Σ A=UΣV^T→AV=UΣV^TV=UΣ A=UΣVT→AV=UΣVTV=UΣ
Σ
Σ
Σ只有对角线上的元素是非零,因此逐一求出对角线上的元素
α
i
α_i
αi即可
A
v
1
=
U
α
1
Av_1=Uα_1
Av1=Uα1、
A
v
2
=
U
α
2
Av_2=Uα_2
Av2=Uα2…
又或者,
-
A = U Σ V T → A T = V Σ U T A=UΣV^T→A^T=VΣU^T A=UΣVT→AT=VΣUT, A A T = U Σ V T V Σ U T = U Σ 2 U T AA^T=UΣV^TVΣU^T=UΣ^2U^T AAT=UΣVTVΣUT=UΣ2UT
-
由于U是 A A T AA^T AAT的特征向量,因此 A A T U = λ u U → A A T = U Σ u U T = U Σ 2 U T AA^TU=λ_uU→AA^T=UΣ_uU^T=UΣ^2U^T AATU=λuU→AAT=UΣuUT=UΣ2UT
-
因此有 Σ 2 = Σ u Σ^2=Σ_u Σ2=Σu, 奇异 值 2 = m × m 的 A A T 方阵的特征值 奇异值²=m×m的AA^T方阵的特征值 奇异值2=m×m的AAT方阵的特征值
另外,
-
A = U Σ V T → A T = V Σ U T A=UΣV^T→A^T=VΣU^T A=UΣVT→AT=VΣUT, A T A = V Σ U T U Σ V T = V Σ 2 V T A^TA=VΣU^TUΣV^T=VΣ^2V^T ATA=VΣUTUΣVT=VΣ2VT
-
由于V是 A T A A^TA ATA的特征向量,因此 A T A V = λ v V → A T A = V Σ v V T = V Σ 2 V T A^TAV=λ_vV→A^TA=VΣ_vV^T=VΣ^2V^T ATAV=λvV→ATA=VΣvVT=VΣ2VT
-
因此有 Σ 2 = Σ v Σ^2=Σ_v Σ2=Σv, 奇异 值 2 = n × n 的 A T A 方阵的特征值 奇异值²=n×n的A^TA方阵的特征值 奇异值2=n×n的ATA方阵的特征值
困惑来了,U矩阵和V矩阵,分别是mxm和nxn,那么U和V 的特征值个数是不一样,U和V的特征值如果不一样,那么奇异值矩阵里的奇异值,到底是用U的特征值还是V的特征值呢????
看了大神的原文评论,似乎是找到了答案,但为什么U和V的非零特征值会相等呢?
他说,左乘A可以得到。。。但。。。可以得到什么?
唉。。。脑子不好,无法凭空想象,可能要回家用纸推导一下
A
T
A
v
=
λ
v
v
A^TAv=λ_vv
ATAv=λvv,左乘A后
(
A
A
T
)
A
v
=
λ
v
(
A
v
)
(AA^T)Av=λ_v(Av)
(AAT)Av=λv(Av),这有什么特殊的吗?那就要结合u来看
A
A
T
u
=
λ
u
u
AA^Tu=λ_uu
AATu=λuu,如果
A
v
=
u
Av=u
Av=u,那就是
λ
u
=
λ
v
λ_u=λ_v
λu=λv
就可以看到,U和V的特征值相等,但关键是:
A
v
=
u
Av=u
Av=u真的相等吗?
em。。。。。这怎么能看出 A v = u Av=u Av=u呢???
不李姐不李姐,真的不李姐
那就要重新寻找转置矩阵的一个重要性质:
A
T
A
A^TA
ATA和
A
A
T
AA^T
AAT的非零特征值相等
假设 λ i λ_i λi是 A A T AA^T AAT的特征值,对应的特征向量为 x x x
则有 A A T x = λ i x AA^Tx=λ_ix AATx=λix,左乘一个 A T A^T AT,即有 A T A ( A T x ) = λ i ( A T x ) A^TA(A^Tx)=λ_i(A^Tx) ATA(ATx)=λi(ATx)
可以看出, A T A A^TA ATA的特征值也是 λ i λ_i λi,虽然特征向量变为了 A T x A^Tx ATx
同理,反过来也是可以论证出 A T A A^TA ATA与 A A T AA^T AAT特征值相等
但下边是比较原理型的解释,但是涉及了很多线性代数的知识
SVD数学推导(严谨复杂没梳理)
重来👉:那么A、U、V、∑之间有什么关系,才能形成奇异值分解 A = U Σ V T A=UΣV^T A=UΣVT的关系呢?
首先,明确V是 A T A A^TA ATA的正交特征向量组(正交矩阵)
A T A A^TA ATA是nxn实对称矩阵,那么假设 A T A A^TA ATA的秩为r,则说明非零特征值也有r个
为什么实对称矩阵的秩等于非零特征值的个数呢?
懒得证了。。。但不理解的话,心里又会有个疙瘩
有个up主说:实对称矩阵的秩r为非零特征值的个数,是因为实对称矩阵可以进行相似对角化,并且相似对角化的过程并不会影响秩,由于相似对角化后的对角矩阵的主对角线元素,就是特征值,那么,主对角线上有几个元素,即为秩,且意味着实对称矩阵的特征值个数也为r
但我有个很大的困惑:即使实对称矩阵A能相似对角化,且相似对角矩阵为B,且秩未改变。
但对角阵B上的元素只是B的特征值,又不是A的特征值,万一A在相似对角化后,特征值个数与B不同呢?因此,秩不变,不代表秩=特征值个数
除非还能说明,实对称矩阵的特征值个数与相似矩阵的特征值个数一致,或与相似矩阵的特征值一致。
如何论证实对称矩阵必定可以相似对角化,且对角阵上的元素即为实对称矩阵的特征值呢?
这里要拆解为3个待探索的问题:
- 什么是相似对角化?(这个比较好理解)
- 为什么实对称矩阵必定可以相似对角化?(不好理解)
- 为什么对角阵上的元素为实对称矩阵的特征值?(就没去理解)
那么, V 原 = [ v 1 , v 2 , . . . v r ] V_原 = [v_1,v_2,...v_r] V原=[v1,v2,...vr],也有r个特征向量,且相互正交 A T A v i = λ i v i A^TAv_i=λ_iv_i ATAvi=λivi, λ i 是 v i 对应 λ_i是v_i对应 λi是vi对应的特征值令 A v i Av_i Avi是mx1矩阵,设 u i = A v i ∣ ∣ A v i ∣ ∣ u_i=\frac{Av_i}{||Av_i||} ui=∣∣Avi∣∣Avi ∣ ∣ A v i ∣ ∣ 2 = ( A v i ) T ( A v i ) = v i T A T A v i = v i T λ i v i = λ i v i T v i = λ i ||Av_i||^2=(Av_i)^T(Av_i)=v_i^TA^TAv_i=v_i^Tλ_iv_i=λ_iv_i^Tv_i=λ_i ∣∣Avi∣∣2=(Avi)T(Avi)=viTATAvi=viTλivi=λiviTvi=λi
u i = A v i ∣ ∣ A v i ∣ ∣ = A v i λ i u_i=\frac{Av_i}{||Av_i||}=\frac{Av_i}{\sqrt{λ_i}} ui=∣∣Avi∣∣Avi=λiAvi
令 σ i = λ i σ_i=\sqrt{λ_i} σi=λi
则
σ
i
u
i
=
A
v
i
σ_iu_i=Av_i
σiui=Avi

头疼,无法理解更多了
只能说明,这个U和V都是补充成各自的mxm和nxn矩阵的正交矩阵
奇异值分解的降维意义
为什么奇异值分解,可以进行降维呢?
主要还是参考矩阵的特征分解时的降维意义。
不过,这只是一种比较数理方面的解释,B站有个博主,用了非常生动形象的动画效果,演示了降维的操作及意义!
B站小学长课堂
当时我在高铁的渣渣网络上看到时,虽然卡的一匹,但依然惊叹到:世间有如此博主,实乃学渣之幸事!
总之,到这里,奇异值分解内容,算是学习结束了
撒花~🌼
不不不,从PCA穿越回来的我,还是深深谴责了自己的浮躁
SVD究竟是怎样降维的,还需要再深思一下。
A是mxn的矩阵,U是mxm的方阵,V是nxn的方阵,∑是一个mxn的奇异值矩阵,且只有对角线上的元素为非零元素,并且对角线上的奇异值²=U的特征值,或=V的特征值。
如果降维选取的是前K个奇异值,那么U和V都会相应地裁剪成mxk和kxn的形式
也就是,U只保留前K列的数据,而 V T V^T VT只保留前K行的数据,实际也是V保留了前K列
最终合成的数据还是mxn形式文章来源:https://www.toymoban.com/news/detail-724875.html
但说实话,它最终保留的前K个特征值分别是什么,尤其应用在压缩图像上,它压缩后保留的具体是什么信息,删掉的又是些什么信息,我目前还没理解文章来源地址https://www.toymoban.com/news/detail-724875.html
到了这里,关于机器学习——奇异值分解二(特征分解+SVD纯理解,头疼系列)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!