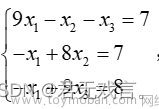高斯消去法解方程组的fortran程序实现
许多实际问题的解决,常常要化为求解线性代数方程组;例如,用最小二乘法处理测量结果和用差分法求解偏微分方程时,都会得到线性方程组;同时,很多物理学的问题最后也要归结到求矩阵的特征值和特征向量。因此,线性代数代数计算方法是一类很重要,应用很普遍的计算方法。
解线性方程组的各种方法中,高斯消去法具有通用性好,运算量小的优点,在编程解线性方程组方面应用广泛。
例如,用高斯法求解下面线性代数方程组:
A
x
=
b
(
1
)
Ax= b \qquad(1)
Ax=b(1)
其中,
A
A
A为
n
×
n
n\times n
n×n矩阵,x是解向量,b是方程组右边n维列向量。
程序参数说明:
A:
输入参数,N*N1个元素的二维实数组,存放由(1)式的系数矩阵和右端的列向量所组成的增广矩阵,存储方式是按列存放,该参数也是输出参数,其N1列存放解向量。
N:
整变量,输入参数,方程组的阶数。
N1:
整变量,输入参数,N1=N+1
EP:
实参数,输入参数,控制常数,通常为比较小的正实数
KWJI:
整变量,输出参数,标志。当矩阵
A
(
k
−
1
)
A^{(k-1)}
A(k−1)(其意义见下面内容)的第k列元素
a
k
k
(
k
−
1
)
a_{kk}^{(k-1)}
akk(k−1),
a
k
+
1
,
k
(
k
−
1
)
a_{k+1,k}^{(k-1)}
ak+1,k(k−1),…,
a
n
,
k
(
k
−
1
)
a_{n,k}^{(k-1)}
an,k(k−1)的绝对值均小于EP时,令KWJI=1,这时认为组(1)无解;否则令KWJI=0.
方法简介:
高斯消去法有两部分组成,向前过程和回代过程。在向前过程中,用一系列初等变换作用于A,把A化成单位上三角阵U.
高斯消去法的向前过程由n步组成,令
A
k
−
1
A^{k-1}
Ak−1是第k步开始的矩阵,令
A
0
=
A
A^{0}=A
A0=A,
A
n
=
U
A^{n}=U
An=U;又令
a
i
j
(
k
−
1
)
a_{ij}^{(k-1)}
aij(k−1)表示矩阵
A
(
k
−
1
)
A^{(k-1)}
A(k−1)的第i行第j列的元素(即(i,j)元素);假设向前过程已经进行了k-1步,得到矩阵
A
(
k
−
1
)
A^{(k-1)}
A(k−1),有形式:
右端项为:
于是向前过程的第k步得到的矩阵
A
k
A^{k}
Ak及右端项
b
k
b^{k}
bk的元素由下列公式确定:
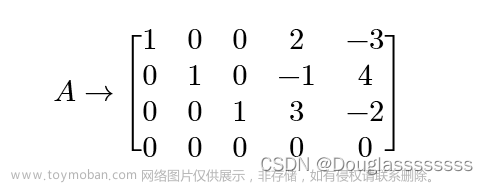
按这种步骤进行到k=n,则矩阵
A
(
n
)
A^{(n)}
A(n)为为单位上三角矩阵;
回代过程的目的是求出组(1)的解。其计算公式如下:
(4)式中的元素
a
k
k
(
k
−
1
)
a_{kk}^{(k-1)}
akk(k−1)叫做向前过程第k步上的主元。在计算过程中,他可能为零,使得计算无法进行。因此本程序采用从
a
k
k
(
k
−
1
)
a_{kk}^{(k-1)}
akk(k−1)开始按次序在
a
k
k
(
k
−
1
)
a_{kk}^{(k-1)}
akk(k−1),
a
k
+
1
,
k
(
k
−
1
)
a_{k+1,k}^{(k-1)}
ak+1,k(k−1),…,
a
n
,
k
(
k
−
1
)
a_{n,k}^{(k-1)}
an,k(k−1)中寻找第一份非0元作为主元,用行交换来完成。文章来源:https://www.toymoban.com/news/detail-724881.html
程序代码:
参考资料:刘德贵-《fortran算法汇编》文章来源地址https://www.toymoban.com/news/detail-724881.html
到了这里,关于高斯消去法解线性方程组的fortran程序实现的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!