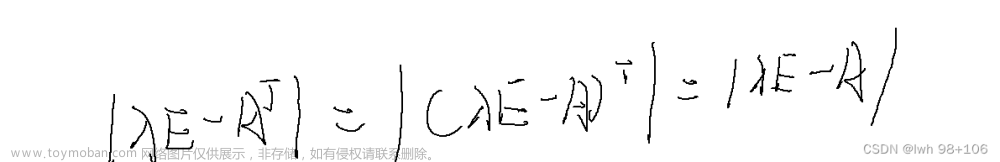线性代数｜余子式和代数余子式的性质-Toy模板网

这篇具有很好参考价值的文章主要介绍了线性代数｜余子式和代数余子式的性质。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前置知识：

【定义】n阶行列式
行列式的性质
阶梯形行列式的性质
【定义】余子式和代数余子式

引理1　设
$\begin{vmatrix} a_{11} & \cdots & a_{1k} & & & \\ \vdots & & \vdots & & 0 & \\ a_{k1} & \cdots & a_{kk} & & & \\ c_{11} & \cdots & c_{1k} & b_{11} & \cdots & b_{1n} \\ \vdots & & \vdots & \vdots & & \vdots \\ c_{n1} & \cdots & c_{nk} & b_{n1} & \cdots & b_{nn} \\ \end{vmatrix}$

$D_1 = det(a_{ij}) = \begin{vmatrix} a_{11} & \cdots & a_{1k} \\ \vdots & & \vdots \\ a_{k1} & \cdots & a_{kk} \\ \end{vmatrix}, \hspace{1em} D_2 = det(b_{ij}) = \begin{vmatrix} b_{11} & \cdots & b_{1k} \\ \vdots & & \vdots \\ b_{k1} & \cdots & b_{kk} \\ \end{vmatrix}$

满足 $D = D_1 D_2$ 。

证明见 “阶梯形行列式的性质”。

引理2　对换行列式的两行（列），行列式变号。

证明见 “行列式的性质”。

引理3　若行列式中某一行（列）的元素都是两数之和，则行列式关于该行（列）可分解为两个行列式。

证明见 “行列式的性质”。

引理4　如果行列式有两行（列）完全相同，则此行列式等于零。

证明见 “行列式的性质”。

我们考虑用低阶行列式来表示高阶行列式的问题。首先，我们考虑一种特殊情况；根据余子式和代数余子式的定义，有引理及证明如下：

引理　一个 $n$ 阶行列式，如果其中第 $i$ 行所有元素除 $(i, j)$ 元 $a_{ij}$ 外都为零，那么这行列式等于 $a_{ij}$ 与它的代数余子式的乘积，即
$D = a_{ij} A_{ij}$

证明　首先证 $(i, j) = (1, 1)$ 的情形。此时
$\begin{vmatrix} a_{11} & 0 & \cdots & 0 \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix}$
根据引理 1 可知 $D = a_{11} M_{11}$ ，于是有 $A_{11} = (-1)^{i+j} M_{11} = M_{11}$ ，从而
$D = a_{11} A_{11}$
再证一般情形，此时
$\begin{vmatrix} a_{11} & \cdots & a_{1j} & \cdots & a_{1n} \\ \vdots & & \vdots & & \vdots \\ 0 & \cdots & a_{ij} & \cdots & 0 \\ \vdots & & \vdots & & \vdots \\ a_{n1} & \cdots & a_{nj} & \cdots & a_{nn} \end{vmatrix}$
为了利用前面的结果，将 $D$ 的第 $i$ 行依次与第 $i - 1$ 行、第 $i - 2$ 行……第 $1$ 行对换，这样数 $a_{ij}$ 就换成了 $(1, j)$ 元，对换次数为 $i - 1$ ；在将 $D$ 的第 $j$ 列依次与第 $j - 1$ 列、第 $j - 2$ 列……第 $1$ 列对换，这样数 $a_{ij}$ 就换成了 $(1, 1)$ 元，对换次数为 $j - 1$ 。根据引理 2，因为累计进行 $i + j - 2$ 次对换，所以所得行列式 $D_1 = (-1)^{i+j-2} D = (-1)^{i+j} D$ ，而 $D_1$ 中 $(1, 1)$ 元的余子式就是 $D$ 中 $(i, j)$ 元的余子式 $M_{ij}$ 。

由于 $D_1$ 的 $(1, 1)$ 元为 $a_{ij}$ ，第 $1$ 行其余元素都为 $0$ ，利用已证 $(i, j) = (1, 1)$ 的特殊情形，有
$D_1 = a_{ij} M_{ij}$
于是
$D = (-1)^{i+j} D_1 = (-1)^{i+j} a_{ij} M_{ij} = a_{ij} A_{ij}$

接着，我们考虑一般情况；根据上述引理，有如下定理和证明：

定理2　行列式等于它的任一行（列）的各元素与其对应的代数余子式的乘积之和，即
$a_{i1} A_{i1} + a_{i2} A_{i2} + \cdots + a_{in} A_{in} \hspace{1em} (i=1,2,\cdots,n)$
或
$a_{1j} A_{1j} + a_{2j} A_{2j} + \cdots + a_{nj} A_{nj} \hspace{1em} (j=1,2,\cdots,n)$

证明　首先证行列式等于它的任一行的个元素与其对应的代数余子式的乘积之和。根据引理 3，可将行列式拆分为 $n$ 个行列式，其中每个行列式中第 $i$ 行仅有一个元素不为 $0$ ，即
$\begin{align*} D & = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} & a_{i2} & \cdots & a_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} \\ & = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} + 0 + \cdots + 0 & 0 + a_{i2} + \cdots + 0 & \cdots & 0 + \cdots + 0+a_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} \\ & = \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ a_{i1} & 0 & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} + \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & a_{i2} & \cdots & 0 \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} + \begin{vmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ \vdots & \vdots & & \vdots \\ 0 & 0 & \cdots & a_{in} \\ \vdots & \vdots & & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{vmatrix} \end{align*}$

根据引理，即得
$a_{i1} A_{i1} + a_{i2} A_{i2} + \cdots + a_{in} A_{in} \hspace{1em} (i=1,2,\cdots,n)$

根据引理 2 ，同理可证行列式等于它的任一列的个元素与其对应的代数余子式的乘积之和。

这个定理叫做行列式按行（按列）展开法则。

根据引理 4，有推论及其证明如下：

推论　行列式某一行（列）的元素与另一行（列）的对应元素的代数余子式乘积之和等于零，即
$a_{i1} A_{j1} + a_{i2} A_{j2} + \cdots a_{in} A_{jn} = 0, \hspace{1em} i \ne j$
或
$a_{1i} A_{1j} + a_{2i} A_{2j} + \cdots a_{ni} A_{nj}, \hspace{1em} i \ne j$

证明　首先证明，行列式某一行的元素与另一行的对应元素的代数余子式乘积之和等于零。设有 $n$ 阶行列式 $D = det(a_{ij})$ ，则它的按第 $j$ 行展开式
$a_{j1} A_{j1} + a_{j2} A_{j2} + \cdots a_{jn} A_{jn}$
因诸 $A_{jk} (k=1,2,\cdots,n)$ 都是先划去了 $D$ 中第 $j$ 行再经计算而得，所以当第 $j$ 行元素依次取为 $b_1,b_2,\cdots,b_n$ 时就有
$D_j = \begin{vmatrix} a_{11} & \cdots & a_{1n} \\ \vdots & & \vdots \\ a_{j-1,1} & \cdots & a_{j-1,n} \\ b_1 & \cdots & b_n \\ a_{j+1,1} & \cdots & a_{j+1,n} \\ \vdots & & \vdots \\ a_{n1} & \cdots & a_{mn} \end{vmatrix} = b_1 A_{j1} + b_2 A_{j2} + \cdots b_n A_{jn}$
这里 $D_j$ 表示除第 $j$ 行外其余各行均与 $D$ 相同的行列式。

特别，当 $b_1,b_2,\cdots,b_n$ 依次取与 $D = det(a_{ij})$ 的第 $i$ 行（ $\ne j$ ）各元素时，上式仍成立。但此时因 $D_j$ 中第 $j$ 行与第 $i$ 行两行相同，根据引理 4， $D_j = 0$ ，从而有
$a_{i1} A_{j1} + a_{i2} A_{j2} + \cdots a_{in} A_{jn} = 0, \hspace{1em} i \ne j$
根据引理 2 ，同理可证行列式某一列的元素与另一列的对应元素的代数余子式乘积之和等于零。

根据定理 2 和推论，可得代数余子式的重要性质如下：
$\sum_{k=1}^n a_{ki} A_{kj} = \begin{cases} D, \hspace{1em} & i = j, \\ 0, \hspace{1em} & i \ne j \end{cases}$
或
$\sum_{k=1}^n a_{ik} A_{jk} = \begin{cases} D, \hspace{1em} & i = j, \\ 0, \hspace{1em} & i \ne j \end{cases}$ 文章来源地址https://www.toymoban.com/news/detail-725292.html