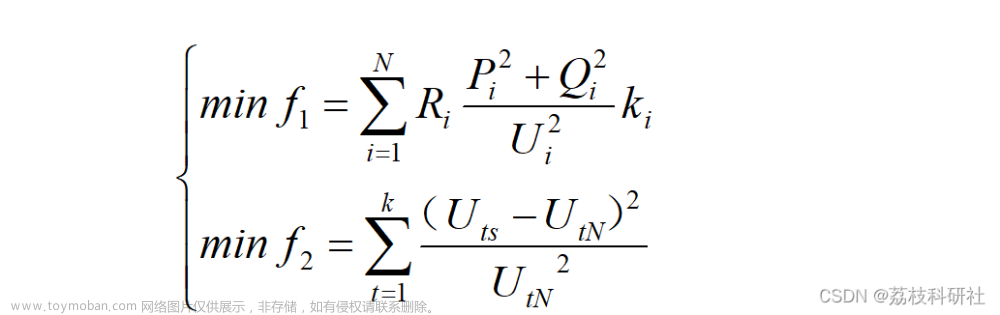多目标优化 | NSGA-Ⅲ（中篇，附MATLAB代码）

上个月我们在多目标优化 | NSGA-Ⅲ（上篇，附MATLAB代码）这篇推文中，为各位回顾了NSGA-Ⅱ，同时也讲解了多目标优化算法NSGA-Ⅲ中的参考点生成方法。今天我们书接上回，为各位讲解NSGA-Ⅲ中的种群个体的自适应归一化操作。

首先需要明确一个问题，为什么需要进行归一化处理？

答：由于后面我们将每一个解和参考点相互联系从而维持种群多样性，参考点又是均匀分布在目标空间的，而每个解的各个目标函数尺度不一样导致解的偏向性不一样，比如目标函数$f_1$的范围为$[0,1]$，目标函数$f_2$的范围为$[0,100]$，那么在联系解和参考点时，$f_1$和$f_2$起的作用就不“公平”了。（参考[7]）

目录

1. 常规归一化操作
2. 种群个体的自适应归一化操作
3. NSGA-Ⅲ代码获取方式
4. 参考文献

常规归一化操作

在生成若干参考点后，接下来需要对种群中个体的目标函数值进行归一化操作。常规归一化操作的公式如下：
$$f_{i,j}^n=\frac{f_{i,j}-f_i^{\min }}{f_i^{\max }-f_i^{\min }}i=1,2,\cdots ,M,j=1,2,\cdots ,N$$
其中，$f_{i,j}^n$表示第$j$个个体第$i$个目标归一化处理后的目标函数值，$f_{i,j}$第$j$个个体第$i$个目标归一化处理前的目标函数值，$f_i^{\min }$表示种群个体中第$i$个目标的最小值目标函数值，$f_i^{\max }$表示种群个体中第$i$个目标的最大值目标函数值，$M$表示目标函数值维数，$N$表示种群数目。

**【举例】**假设种群中有3个个体，这3个体的目标函数值分别为$(1,6)$、$(2,5)$、$(3,4)$，则采用上述公式对这三个个体进行归一化操作的计算过程如下：
$$第1维目标函数值的最小值f_1^{\min }=min(1,2,3)=1$$

$$第1维目标函数值的最大值f_1^{\max }=max(1,2,3)=3$$

$$第2维目标函数值的最小值f_2^{\min }=min(6,5,4)=4$$

$$第2维目标函数值的最大值f_2^{\max }=max(6,5,4)=6$$

$$个体1归一化处理后的第1维目标函数值f_{1,1}^n=\frac{f_{1,1}-f_1^{\min }}{f_1^{\max }-f_1^{\min }}=\frac{1-1}{3-1}=0$$

$$个体1归一化处理后的第2维目标函数值f_{2,1}^n=\frac{f_{2,1}-f_2^{\min }}{f_2^{\max }-f_2^{\min }}=\frac{6-4}{6-4}=1$$

$$个体2归一化处理后的第1维目标函数值f_{1,2}^n=\frac{f_{1,2}-f_1^{\min }}{f_1^{\max }-f_1^{\min }}=\frac{2-1}{3-1}=\frac{1}{2}$$

$$个体2归一化处理后的第2维目标函数值f_{2,2}^n=\frac{f_{2,2}-f_2^{\min }}{f_2^{\max }-f_2^{\min }}=\frac{5-4}{6-4}=\frac{1}{2}$$

$$个体3归一化处理后的第1维目标函数值f_{1,3}^n=\frac{f_{1,3}-f_1^{\min }}{f_1^{\max }-f_1^{\min }}=\frac{3-1}{3-1}=1$$

$$个体3归一化处理后的第2维目标函数值f_{2,3}^n=\frac{f_{2,3}-f_2^{\min }}{f_2^{\max }-f_2^{\min }}=\frac{4-4}{6-4}=0$$

从上述公式和例子中可以看出，归一化处理实际上是将目标函数值放缩在0~1之间。

种群个体的自适应归一化操作

NSGA-Ⅲ中并没有采用常规的归一化操作，而是采用了一种自适应归一化操作，具体步骤如下：

STEP1：计算种群理想点（ideal point）；

STEP2：转换种群目标函数值；

STEP3：计算每个坐标轴对应的极值点（extreme points）；

STEP4：计算超平面与坐标轴的截距；

STEP5：归一化种群目标函数值。

计算种群理想点

种群$S_t$的理想点实际上为${\cup }_{\tau =0}^t{S}_{\tau }$中各维目标函数值的最小值，即$\bar{z}=\left(z_1^{\min },z_2^{\min },\dots ,z_M^{\min }\right)$。其中$\bar{z}$表示理想点，$z_j^{\min }$表示第$i$个目标的最小值目标函数值，$M$表示目标函数值数目，种群$S_t$的理想点计算公式如下：
$$z_j^{\min }=\underset{\mathbf{s}\in \left({\cup }_{\tau =0}^t{S}_{\tau }\right)}{\min }{f}_j(\mathbf{s})$$
**【举例】**假设种群$S_0$中包含4个个体，目标函数数目为3，每个个体的目标函数值分别为(1,5,9),(4,2,8),(3,4,7),(6,1,6)。
$$z_1^{\min }=\underset{\mathbf{s}\in S_0}{\min }{f}_1(\mathbf{s})=\min (1,4,3,6)=1$$

$$z_2^{\min }=\underset{\mathbf{s}\in S_0}{\min }{f}_2(\mathbf{s})=\min (5,2,4,1)=1$$

$$z_3^{\min }=\underset{\mathbf{s}\in S_0}{\min }{f}_3(\mathbf{s})=\min (9,8,7,6)=6$$

则种群$S_0$的理想点为
$$\bar{z}=\left(z_1^{\min },z_2^{\min },z_3^{\min }\right)=(1,1,6)$$

转换种群目标函数值

在计算出理想点后，接下来就可以对种群$S_t$中每个个体的目标函数值进行转换，即每个个体目标函数值减去对应维的理想点目标函数值，其公式如下：
$$f_j^{\prime }(\mathbf{s})=f_j(\mathbf{s})-z_j^{\min }\forall \mathbf{s}\in S_t$$
【举例】承接上例，对4个个体目标函数值进行转换，转换结果如下：
$$个体1转换后的目标函数值=(1-1,5-1,9-6)=(0,4,3)$$

$$个体2转换后的目标函数值=(4-1,2-1,8-6)=(3,1,2)$$

$$个体3转换后的目标函数值=(3-1,4-1,7-6)=(2,3,1)$$

$$个体4转换后的目标函数值=(6-1,1-1,6-6)=(5,0,0)$$

计算每个坐标轴对应的极值点

极值点这部分内容属于自适应归一化操作中最难理解的一部分内容，首先明确一个事项，极值点数目等于目标函数数目。通过对常规归一化操作的学习，我们了解到归一化实际上是在指定范围内进行放缩操作，其中放缩公式的分母即为各个目标函数的最大值与最小值的差值。

而在NSGA-Ⅲ中，归一化采用放缩的思想仍然是不变的，只不过放缩公式的分母不是各个目标函数的最大值与最小值的差值，而是各个坐标轴截距与所对应目标函数最小值的差值。

至于如何计算各个坐标轴截距，就需要极值点进行求解。

关于极值点，个人是这样理解的。极值点中的“极”字，可以理解为“极限”的意思，也就是说无限趋近与指定坐标轴的点。举一个简单的例子，$(1000,1)$比$(1,1)$更趋近于$x$轴。

在上述对于“极限”理解的基础上，极值点的计算公式如下：
$$\begin{array}{c}ASF(x,w)={\max }_{i=1}^M{f}_i^{\prime }(x)/w_i,x\in S_t\\ z^{j,\max }=s:{\mathrm{argmin}}_{s\in S_t}ASF\left(s,w\right),w=(ϵ,\dots ,ϵ),ϵ=10^{-6},w_j=1\end{array}$$
【举例】承接上例，求出3个极值点的计算过程如下：

首先找出趋近于**$x$轴**的极值点，需要注意的是此时$w_1=1$，则$w=(1,10^{-6},10^{-6})$，然后分别计算4个个体的$ASF(x,w)$，
$$个体1的ASF(x_1,w)=\underset{i=1}{\overset{M}{\max }}{f}_i^{\prime }(x)/w_i=max(0/1,4/10^{-6},3/10^{-6})=max(0,6\times 10^6,3\times 10^6)=6\times 10^6$$

$$个体2的ASF(x_2,w)=\underset{i=1}{\overset{M}{\max }}{f}_i^{\prime }(x)/w_i=max(3/1,1/10^{-6},2/10^{-6})=max(3,1\times 10^6,2\times 10^6)=2\times 10^6$$

$$个体3的ASF(x_3,w)=\underset{i=1}{\overset{M}{\max }}{f}_i^{\prime }(x)/w_i=max(2/1,3/10^{-6},1/10^{-6})=max(2,3\times 10^6,1\times 10^6)=3\times 10^6$$

$$个体4的ASF(x_4,w)=\underset{i=1}{\overset{M}{\max }}{f}_i^{\prime }(x)/w_i=max(5/1,0/10^{-6},0/10^{-6})=max(5,0\times 10^6,0\times 10^6)=5$$

在求得4个个体求得的$ASF(x,w)$后，采用下述公式求得第1个极值点：
$$z^{1,\max }=s:{\mathrm{argmin}}_{s\in S_t}ASF\left(s,w\right)=s:\mathrm{argmin}(6\times 10^6,2\times 10^6,3\times 10^6,5)=(5,0,0)$$
即比较4个个体求得的$ASF(x,w)$，发现个体4的$ASF(x,w)$最小。因此第1个极值点即为$(5,0,0)$，即$(5,0,0)$相比于其它点更趋近于**$x$轴**。

按照上述求解步骤，求出另外2个极值点分别为$(2,3,1)$和$(3,1,2)$，即$z^{2,\max }=(2,3,1),z^{3,\max }=(3,1,2)$。

计算超平面与坐标轴的截距

在求得极值点后，接下来通过求解线性方程组即可获取与各个坐标轴的截距。2维空间2个极值点有2个截距，3维空间3个极值点有3个截距，4维空间4个极值点有4个截距，依此类推，n维空间n个极值点有n个截距。

在3维空间中，3个极值点可以形成空间平面。当空间维数大于3时，即形成超平面。

以3维空间为例，截距式平面方程为
$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1$$
假设3个点的坐标分别为$(x_1,y_1,z_1),(x_2,y_2,z_2),(x_3,y_3,z_3)$，则带入上述平面方程，得出如下线性方程组：
{ x 1 a + y 1 b + z 1 c = 1 x 2 a + y 2 b + z 2 c = 1 x 3 a + y 3 b + z 3 c = 1 → [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] [ 1 a 1 b 1 c ] = [ 1 1 1 ] → [ 1 a 1 b 1 c ] = [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] − 1 [ 1 1 1 ] \left\{\begin{array}{l} \frac{x_1}{a}+\frac{y_1}{b}+\frac{z_1}{c}=1 \\ \frac{x_2}{a}+\frac{y_2}{b}+\frac{z_2}{c}=1 \\ \frac{x_3}{a}+\frac{y_3}{b}+\frac{z_3}{c}=1 \end{array} \rightarrow\left[\begin{array}{lll} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{array}\right]\left[\begin{array}{l} \frac{1}{a} \\ \frac{1}{b} \\ \frac{1}{c} \end{array}\right]=\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] \rightarrow\left[\begin{array}{l} \frac{1}{a} \\ \frac{1}{b} \\ \frac{1}{c} \end{array}\right]=\left[\begin{array}{lll} x_1 & y_1 & z_1 \\ x_2 & y_2 & z_2 \\ x_3 & y_3 & z_3 \end{array}\right]^{-1}\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]\right. ⎩ ⎨ ⎧​ax1​​+by1​​+cz1​​=1ax2​​+by2​​+cz2​​=1ax3​​+by3​​+cz3​​=1​→ ​x1​x2​x3​​y1​y2​y3​​z1​z2​z3​​ ​ ​a1​b1​c1​​ ​= ​111​ ​→ ​a1​b1​c1​​ ​= ​x1​x2​x3​​y1​y2​y3​​z1​z2​z3​​ ​−1 ​111​ ​
推广到n维空间，线性方程组如下：
{ f 1 , 1 a 1 + f 2 , 1 a 2 + ⋯ + f n , 1 a n = 1 f 1 , 2 a 1 + f 2 , 2 a 2 + ⋯ + f n , 2 a n = 1 ⋮ f 1 , n a 1 + f 2 , n a 2 + ⋯ + f n , n a n = 1 → [ f 1 , 1 f 2 , 1 ⋯ f n , 1 f 1 , 2 f 2 , 2 ⋯ f n , 2 ⋮ ⋮ ⋱ ⋮ f 1 , n f 2 , n ⋯ f n , n ] [ 1 a 1 1 a 2 ⋮ 1 a n ] = [ 1 1 ⋮ 1 ] → [ 1 a 1 1 a 2 ⋮ 1 a n ] = [ f 1 , 1 f 2 , 1 ⋯ f n , 1 f 1 , 2 f 2 , 2 ⋯ f n , 2 ⋮ ⋮ ⋱ ⋮ f 1 , n f 2 , n ⋯ f n , n ] [ 1 1 ⋮ 1 ] \left\{\begin{array}{c} \frac{f_{1,1}}{a_1}+\frac{f_{2,1}}{a_2}+\cdots+\frac{f_{n, 1}}{a_n}=1 \\ \frac{f_{1,2}}{a_1}+\frac{f_{2,2}}{a_2}+\cdots+\frac{f_{n, 2}}{a_n}=1 \\ \vdots \\ \frac{f_{1, n}}{a_1}+\frac{f_{2, n}}{a_2}+\cdots+\frac{f_{n, n}}{a_n}=1 \end{array} \rightarrow\left[\begin{array}{cccc} f_{1,1} & f_{2,1} & \cdots & f_{n, 1} \\ f_{1,2} & f_{2,2} & \cdots & f_{n, 2} \\ \vdots & \vdots & \ddots & \vdots \\ f_{1, n} & f_{2, n} & \cdots & f_{n, n} \end{array}\right]\left[\begin{array}{c} \frac{1}{a_1} \\ \frac{1}{a_2} \\ \vdots \\ \frac{1}{a_n} \end{array}\right]=\left[\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right] \rightarrow\left[\begin{array}{c} \frac{1}{a_1} \\ \frac{1}{a_2} \\ \vdots \\ \frac{1}{a_n} \end{array}\right]=\left[\begin{array}{cccc} f_{1,1} & f_{2,1} & \cdots & f_{n, 1} \\ f_{1,2} & f_{2,2} & \cdots & f_{n, 2} \\ \vdots & \vdots & \ddots & \vdots \\ f_{1, n} & f_{2, n} & \cdots & f_{n, n} \end{array}\right]\left[\begin{array}{c} 1 \\ 1 \\ \vdots \\ 1 \end{array}\right]\right. ⎩ ⎨ ⎧​a1​f1,1​​+a2​f2,1​​+⋯+an​fn,1​​=1a1​f1,2​​+a2​f2,2​​+⋯+an​fn,2​​=1⋮a1​f1,n​​+a2​f2,n​​+⋯+an​fn,n​​=1​→ ​f1,1​f1,2​⋮f1,n​​f2,1​f2,2​⋮f2,n​​⋯⋯⋱⋯​fn,1​fn,2​⋮fn,n​​ ​ ​a1​1​a2​1​⋮an​1​​ ​= ​11⋮1​ ​→ ​a1​1​a2​1​⋮an​1​​ ​= ​f1,1​f1,2​⋮f1,n​​f2,1​f2,2​⋮f2,n​​⋯⋯⋱⋯​fn,1​fn,2​⋮fn,n​​ ​ ​11⋮1​ ​

**【举例】**承接上例，计算出上述3个极值点$(5,0,0),(2,3,1),(3,1,2)$所构成的平面与各个坐标轴的截距。
{ 5 a + 0 b + 0 c = 1 2 a + 3 b + 1 c = 1 3 a + 1 b + 2 c = 1 → [ 5 0 0 2 3 1 3 1 2 ] [ 1 a 1 b 1 c ] = [ 1 1 1 ] → [ 1 a 1 b 1 c ] = [ 5 0 0 2 3 1 3 1 2 ] − 1 [ 1 1 1 ] = [ 0.2 0 0 − 0.04 0.4 − 0.2 − 0.28 − 0.2 0.6 ] [ 1 1 1 ] = [ 0.2 0.16 0.12 ] \left\{\begin{array}{l} \frac{5}{a}+\frac{0}{b}+\frac{0}{c}=1 \\ \frac{2}{a}+\frac{3}{b}+\frac{1}{c}=1 \\ \frac{3}{a}+\frac{1}{b}+\frac{2}{c}=1 \end{array} \rightarrow\left[\begin{array}{lll} 5 & 0 & 0 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{array}\right]\left[\begin{array}{l} \frac{1}{a} \\ \frac{1}{b} \\ \frac{1}{c} \end{array}\right]=\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right] \rightarrow\left[\begin{array}{l} \frac{1}{a} \\ \frac{1}{b} \\ \frac{1}{c} \end{array}\right]=\left[\begin{array}{lll} 5 & 0 & 0 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{array}\right]^{-1}\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]=\left[\begin{array}{ccc} 0.2 & 0 & 0 \\ -0.04 & 0.4 & -0.2 \\ -0.28 & -0.2 & 0.6 \end{array}\right]\left[\begin{array}{l} 1 \\ 1 \\ 1 \end{array}\right]=\left[\begin{array}{c} 0.2 \\ 0.16 \\ 0.12 \end{array}\right]\right. ⎩ ⎨ ⎧​a5​+b0​+c0​=1a2​+b3​+c1​=1a3​+b1​+c2​=1​→ ​523​031​012​ ​ ​a1​b1​c1​​ ​= ​111​ ​→ ​a1​b1​c1​​ ​= ​523​031​012​ ​−1 ​111​ ​= ​0.2−0.04−0.28​00.4−0.2​0−0.20.6​ ​ ​111​ ​= ​0.20.160.12​ ​

[ 1 a 1 b 1 c ] = [ 0.2 0.16 0.12 ] → [ a b c ] = [ 5 6.25 8.33 ] \left[\begin{array}{l} \frac{1}{a} \\ \frac{1}{b} \\ \frac{1}{c} \end{array}\right]=\left[\begin{array}{c} 0.2 \\ 0.16 \\ 0.12 \end{array}\right] \rightarrow\left[\begin{array}{l} a \\ b \\ c \end{array}\right]=\left[\begin{array}{c} 5 \\ 6.25 \\ 8.33 \end{array}\right] ​a1​b1​c1​​ ​= ​0.20.160.12​ ​→ ​abc​ ​= ​56.258.33​ ​

则3个极值点$(5,0,0),(2,3,1),(3,1,2)$所构成的平面与$xyz$坐标轴的截距分别为$a=5,b=6.25,c=8.33$。

极值点与截距的示意图如下图所示：

归一化种群目标函数值

最后一步是对种群中每个个体每一维度的目标函数值进行归一化处理，实际上就是使用转换后的目标函数值除以截距。
$$f_i^n(\mathbf{x})=\frac{f_i^{\prime }(\mathbf{x})}{a_i-z_i^{\min }}=\frac{f_i(\mathbf{x})-z_i^{\min }}{a_i-z_i^{\min }},\text{ for }i=1,2,\dots ,M$$
【举例】承接上例，4个个体归一化后各个维度的目标函数值分别如下：
$$个体1第1个目标转换后的目标函数值f_1^n({\mathbf{x}}_1)=\frac{f_1^{\prime }({\mathbf{x}}_1)}{a}=\frac{0}{5}=0$$

$$个体1第2个目标转换后的目标函数值f_2^n({\mathbf{x}}_1)=\frac{f_2^{\prime }({\mathbf{x}}_1)}{a}=\frac{4}{6.25}=0.64$$

$$个体1第3个目标转换后的目标函数值f_3^n({\mathbf{x}}_1)=\frac{f_3^{\prime }({\mathbf{x}}_1)}{a}=\frac{3}{8.33}=0.36$$

则个体1归一化后的目标函数值为$f^n({\mathbf{x}}_1)=(0,0.64,0.36)$。

同理，个体2归一化后的目标函数值为$f^n({\mathbf{x}}_2)=(0.6,0.16,0.24)$，个体3归一化后的目标函数值为$f^n({\mathbf{x}}_3)=(0.4,0.48,0.12)$，个体4归一化后的目标函数值为$f^n({\mathbf{x}}_4)=(1,0,0)$。

种群自适应归一化操作伪代码

自适应归一化操作伪代码如下：

其中，第2行计算理想点的公式，应该改为$z_j^{\min }={\min }_{\mathbf{s}\in \left({\cup }_{\tau =0}^t{S}_{\tau }\right)}{f}_j(\mathbf{s})$。

NSGA-Ⅲ代码获取方式

https://yarpiz.com/456/ypea126-nsga3

参考文献

1. Katoch S, Chauhan S S, Kumar V. A review on genetic algorithm: past, present, and future[J]. Multimedia Tools and Applications, 2021, 80: 8091-8126.
2. Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE transactions on evolutionary computation, 2002, 6(2): 182-197.
3. Deb K, Jain H. An evolutionary many-objective optimization algorithm using reference-point-based nondominated sorting approach, part I: solving problems with box constraints[J]. IEEE transactions on evolutionary computation, 2013, 18(4): 577-601.
4. Tian Y, Cheng R, Zhang X, et al. PlatEMO: A MATLAB platform for evolutionary multi-objective optimization [educational forum][J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87.
5. Mostapha Kalami Heris, NSGA-III: Non-dominated Sorting Genetic Algorithm, the Third Version — MATLAB Implementation (URL: https://yarpiz.com/456/ypea126-nsga3), Yarpiz, 2016.
6. Das I, Dennis J E. Normal-boundary intersection: A new method for generating the Pareto surface in nonlinear multicriteria optimization problems[J]. SIAM journal on optimization, 1998, 8(3): 631-657.
7. 遗传算法之NSGA-III原理分析和代码解读（https://zhuanlan.zhihu.com/p/146618031）

想快速入门智能优化算法的小伙伴可以阅读我们的书籍，本书对算法的讲解详细易懂，对代码的注释也十分完备。

OK，今天就到这里啦。我们已经推出粉丝交流群，各位小伙伴赶快加入吧！！！

咱们下期再见

近期你可能错过了的好文章

新书上架 | 《MATLAB智能优化算法：从写代码到算法思想》

优化算法 | 灰狼优化算法（文末有福利）

优化算法 | 鲸鱼优化算法

遗传算法（GA）求解带时间窗的车辆路径（VRPTW）问题MATLAB代码

粒子群优化算法（PSO）求解带时间窗的车辆路径问题（VRPTW）MATLAB代码

公众号：优化算法交流地
知乎 | bilibili | CSDN：随心390文章来源地址https://www.toymoban.com/news/detail-725381.html

到了这里，关于多目标优化 | NSGA-Ⅲ（中篇，附MATLAB代码）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！