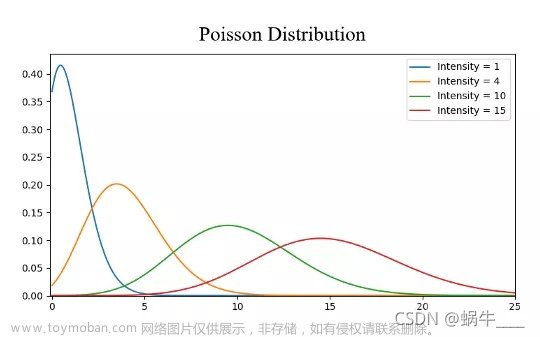
一个正态总体的抽样分布
统计量: X ‾ = 1 n ∑ i = 1 n X i , 其 中 X i ~ N ( μ , σ 2 ) \overline{X}= \cfrac{1}{n}\sum_{i=1}^nX_{i},其中X_{i}\text{\textasciitilde} N(\mu,{\sigma^{2}} ) X=n1i=1∑nXi,其中Xi~N(μ,σ2) S 2 = 1 n − 1 ∑ i = 1 n ( X i − X ‾ ) 2 S^2= \cfrac{1}{n-1}\sum_{i=1}^n(X_{i}-\overline{X})^2 S2=n−11i=1∑n(Xi−X)2推论·:文章来源地址https://www.toymoban.com/news/detail-725450.html
- X ‾ ~ N ( μ , σ 2 n ) 证 明 : X ‾ = 1 n ∑ i = 1 n X i ~ N ( 1 n ∑ i = 1 n μ , ∑ i = 1 n σ 2 n 2 ) = N ( μ , σ 2 n ) \overline{X} \text{\textasciitilde} N(\mu,\cfrac{\sigma^{2}}{n})\\ \begin{aligned} 证明: \overline{X}&= \cfrac{1}{n}\sum_{i=1}^nX_{i} \\& \text{\textasciitilde} N( \cfrac{1}{n}\sum_{i=1}^n\mu, \sum_{i=1}^n\cfrac{\sigma^{2}}{n^2})\\ &=N(\mu,\cfrac{\sigma^{2}}{n})\end{aligned} X~N(μ,nσ2)证明:X=n1i=1∑n
文章来源:https://www.toymoban.com/news/detail-725450.html
到了这里,关于概率论与数理统计:正态分布相关推论及推导(更新ing)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!