【数据结构】二叉树中的递归问题（超详细画图~）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】二叉树中的递归问题（超详细画图~）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【数据结构】二叉树中的递归问题（超详细画图~）,数据结构,数据结构,开发语言,c语言

和光同尘_我的个人主页不管风吹浪打，胜似闲庭信步。 --毛泽东

🕯️前言

我本来还说上节难来着，没想到这节更难🥲
不过我既然会了保证xdm也能看懂👍

1. 前置说明

首先回顾下二叉树的概念

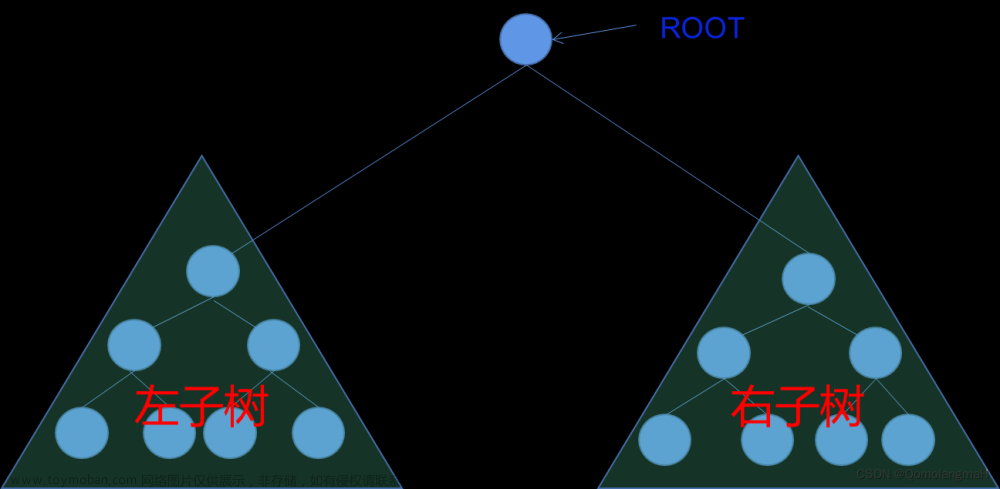
二叉树是由:空树或者非空树（根节点，根节点的左子树、根节点的右子树）组成的

【数据结构】二叉树中的递归问题（超详细画图~）,数据结构,数据结构,开发语言,c语言
从概念中可以看出，二叉树定义是递归式的，后面的思路都是基于此概念实现的

2. 二叉树的遍历

2.1. 前序、中序和后序遍历

二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。
按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。

中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。

后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

前序遍历示意（打印访问结果）：

void PrevOrder(BinaryTreeNode* root) 
{
	if (root == NULL) {
		printf("NULL ");
		
		return;
	}

	printf("%d ", root->val);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

逻辑示意

【数据结构】二叉树中的递归问题（超详细画图~）,数据结构,数据结构,开发语言,c语言

中序后序画不动了…太麻烦了🥲

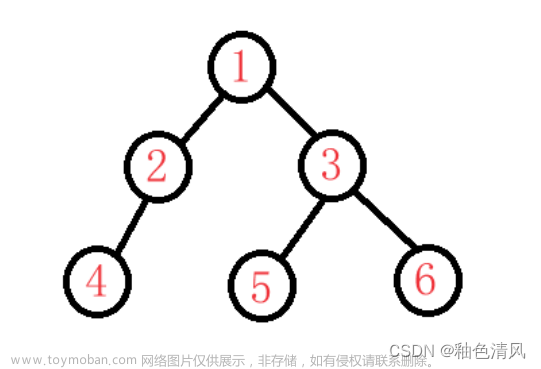
前序、中序、后序的差别就是访问一棵树的顺序，在上图中访问根为1的树时，根据前序根、左、右的顺序，我们先访问了根节点1，而后访问1的左子树，即根为2的节点，而后又先访问了根节点2，完成堆根节点2、左右子树的访问后、才能回退到对节点1右子树的访问……
而如果是中序的话，访问根为1的树时，会直接从根节点1的左子树开始，即根为2的数，完成对2的左右子树、根的访问，才会访问根节点1…
明白了这些我们才能理解后面递归问题的思路

3. 二叉树的简单递归问题

3.1. 求二叉树节点个数

对于这个整体问题，我们可以将其分化成每个树之间联系的小问题
对于每棵树来说，树的节点总和等于根节点+左右子树节点数量的和，即左右子树节点数+1
因此可以得到下面这段代码：

int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

递归问题的代码通常比较短，我们可以通过画图理解其逻辑
以这样的二叉树为例

【数据结构】二叉树中的递归问题（超详细画图~）,数据结构,数据结构,开发语言,c语言

3.2. 求叶子节点个数

这道题与上面的思路类似，同样时树的叶子结点数量等于左右子树叶子节点的数量之和，只需要多加一个判断是否为叶子节点即可。

int TreeLeafSize(BTNode* root)
{
	if(root==NULL)
		return 0;
	if(root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right) + 1;
}

3.3. 求第K层节点个数（根节点为第1层）

这个比起前两道又加了一丢丢难度，不过我们还是一样的思路：

当前树的第K层即为左子树的第k-1层和右子树的k-1层

int TreeKLevel(BTNode* root, int k)
{
	assert(k > 0);

	if (root == NULL)
		return 0;
	if (k == 1)
		return 1;
	return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}

3.4. 单值二叉树

如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树
只有给定的树是单值二叉树时，才返回 true；否则返回 false。
力扣—单值二叉树

这道题又有了一丢丢的变化，我们先按之前的思路，每个节点都相同，即每个树的根都等于左右子树的根，函数要求返回bool值，也就是 根=左子树的根 && 根=右子树的根为真可是这样的话每个树会有：两个子树，只有左、右子树，没有子树；相等，不相等一共8种情况，这也太复杂了😵‍💫
但是我们又会发现，叶子结点对应的树必返回真，那么我们只需要判断为假，即不相等的情况，就可以判断整体的真假，又因为我们不确定是否有左右子树，因此分情况讨论：
左子树存在，根不等于左子树的根，返回假；
右子树存在，根不等于右子树的根，返回假；

我们就得到了这段代码：

bool isUnivalTree(struct TreeNode* root) {

	//叶子结点对应的树返回真
	if (root == NULL)
		return true;

	//左子树存在，根不等于左子树的根，返回假；
	if (root->left != NULL && root->val != root->left->val)
		return false;

	//右子树存在，根不等于右子树的根，返回假；
	if (root->right != NULL && root->val != root->right->val)
		return false;
		
	return isUnivalTree(root->left) && isUnivalTree(root->right);
}