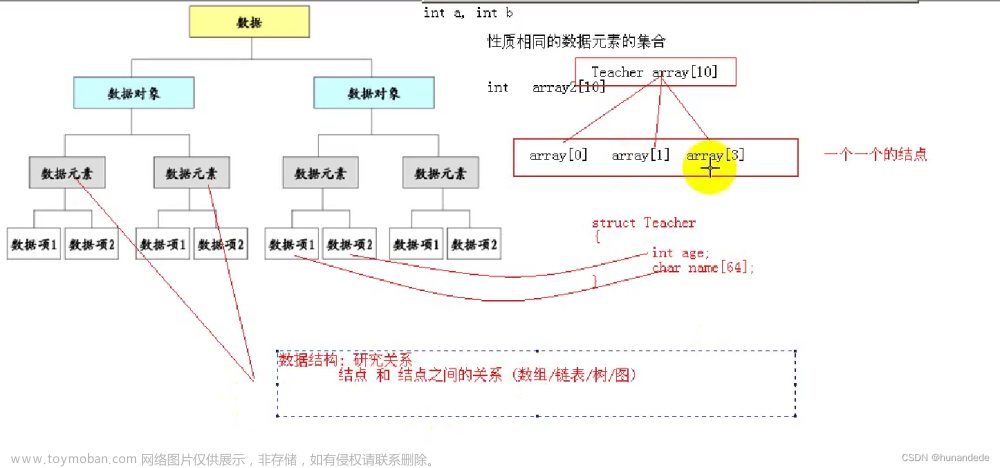
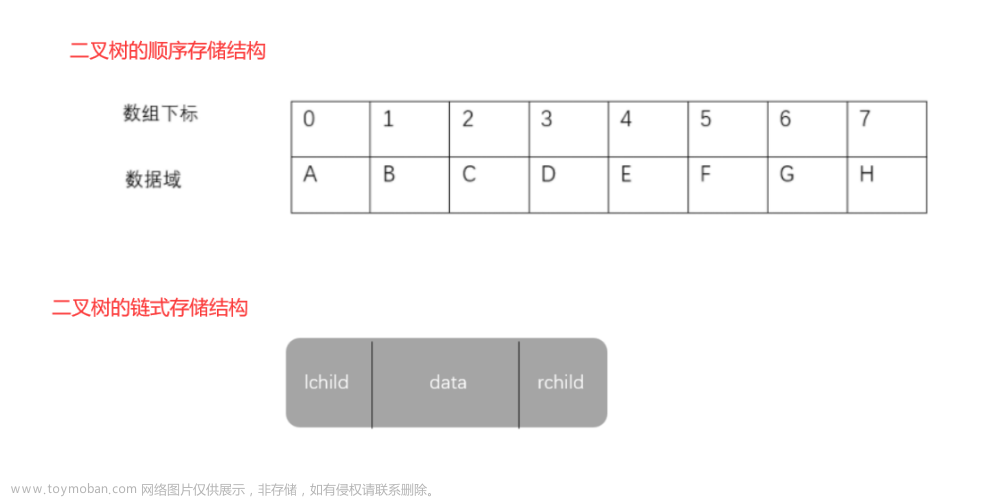
1.单调栈定义:栈内元素按照递增(递减)顺序排列的栈。
单调栈分为单调递增栈和单调递减栈。
单调递增栈:从栈顶到栈底数据是从小到大(栈顶元素最小)
单调递减栈:从栈顶到栈底数据是从大到小(栈顶元素最大)
2.模拟实现一个单调递增栈:
有一组数8,3,6,12。从左到右依次入栈,如果栈为空或入栈元素小于栈顶元素,入栈。
(1).8入栈时,栈为空,直接入栈,栈内元素为8.
(2).3入栈时,栈顶元素为8 > 3,入栈,栈内元素为8,3.
(3).6入栈时,栈顶元素为3 < 6, 则3出栈,此时栈顶元素为 8 > 6 ,则 6入栈,栈内元素为8,6。
(4)12入栈时,栈顶元素为6 < 12,则6出栈,此时栈顶元素为 8 < 12,栈顶元素8继续出栈,此时栈为空,12入栈,栈内元素为12.
3.适用问题:
通常解决前后元素大小关系时使用单调栈。
4.例题:
(1).单调栈(【模板】单调栈 - 洛谷)
给出项数为 n 的整数数列 a1…n。
定义函数 f(i) 代表数列中第 i个元素之后第一个大于 ai 的元素的下标,即 f(i)=mini<j≤n,aj>ai{j}。若不存在,则 f(i)=0。
试求出 f(1…n)。
输入格式
第一行一个正整数 n。
第二行 n 个正整数 a1…n。
输出格式
一行 n 个整数 f(1…n) 的值。
输入输出样例
输入 #1
5 1 4 2 3 5
输出 #1
2 5 4 5 0
说明/提示
【数据规模与约定】
对于 30% 的数据,n ≤ 100;
对于 60% 的数据,n ≤ 5×10^3 ;
对于100% 的数据,1≤n≤3×10^6,1≤ai≤10^9。
AC代码:
#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;
const int N = 3 * 1e6 + 10;
stack<int> v; //存下标
int a[N], f[N]; //a数组储存原数,f数组储存结果下标
int main()
{
std::ios::sync_with_stdio(false); //加速,避免超时
int n;
cin >> n;
for(int i = 1; i <= n; i++ )
cin >> a[i];
for(int i = n; i >= 1; i-- ) //从后向前
{
while(!v.empty() && a[v.top()] <= a[i] ) //栈不为空,栈顶元素比当前元素小,删除栈顶
v.pop();
f[i] = v.empty() ? 0 : v.top(); //栈为空,输出0,非空,栈顶即为答案元素下标
v.push(i); //当前元素下标入栈
}
for(int i = 1; i <= n; i++ ) //正序输出
cout << f[i] <<" ";
return 0;
}
(2).直方图中最大的矩形(131. 直方图中最大的矩形 - AcWing题库)
直方图是由在公共基线处对齐的一系列矩形组成的多边形。
矩形具有相等的宽度,但可以具有不同的高度。
例如,图例左侧显示了由高度为 2,1,4,5,1,3,3 的矩形组成的直方图,矩形的宽度都为 1:

通常,直方图用于表示离散分布,例如,文本中字符的频率。
现在,请你计算在公共基线处对齐的直方图中最大矩形的面积。
图例右图显示了所描绘直方图的最大对齐矩形。
输入格式
输入包含几个测试用例。
每个测试用例占据一行,用以描述一个直方图,并以整数 n 开始,表示组成直方图的矩形数目。
然后跟随 n 个整数 h1,…,hn。
这些数字以从左到右的顺序表示直方图的各个矩形的高度。
每个矩形的宽度为 1。
同行数字用空格隔开。
当输入用例为 n=0时,结束输入,且该用例不用考虑。
输出格式
对于每一个测试用例,输出一个整数,代表指定直方图中最大矩形的区域面积。
每个数据占一行。
请注意,此矩形必须在公共基线处对齐。文章来源:https://www.toymoban.com/news/detail-726051.html
数据范围
1≤n≤100000,
0≤hi≤1000000000文章来源地址https://www.toymoban.com/news/detail-726051.html
输入样例:
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出样例:
8
4000AC代码:
#include <iostream>
#include <algorithm>
#include <stack>
using namespace std;
typedef unsigned long long ull;
const int N = 1e5 + 10;
ull a[N],l[N],r[N]; //a存原数组,l存左边第一个比原数小的下标, r存右边第一个比原数小的下标
int n;
int main()
{
while(cin >> n && n)
{
for(int i = 0; i < n; i++)
cin >> a[i];
stack<ull>s;
ull ans = 0;
a[n]=0; //最后一个
s.push(-1); //第一个
for(int i = 0; i <= n; i++)
{
while(!s.empty() && a[s.top()] > a[i]) //单调递减栈
{
r[s.top()] = i; //被弹出的即为右边第一个比原数小的元素,存下标
s.pop();
}
if(!s.empty())
l[i] = s.top(); //左边第一个比原数小的元素下标即为栈顶元素下标
s.push(i);
}
for(int i = 0 ; i <= n; i++)
{
ans = max( ans, (ull)(r[i] - l[i] - 1) * a[i]); //更新最大值
}
cout << ans << endl;
}
return 0;
}到了这里,关于[数据结构]---单调栈的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!