LU分解
LU分解是旨在将某个矩阵表示为两个或多个矩阵的乘积。
LU分解是将矩阵表示为 A A A= L L L U U U,其中 L L L 矩阵 代表Lower Triangular(下三角矩阵), U U U 矩阵 代表Upper Triangular(上三角矩阵)。形象一点就相当于写为 A = ◣ ∗ ◥ A=◣*◥ A=◣∗◥。
LU分解步骤
1. 求解U矩阵
先求U矩阵,再求L矩阵。
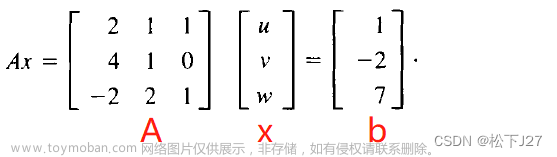
若 A X = b AX=b AX=b是一个非奇异系统,那么高斯消元法将A化简为一个上三角矩阵。
例如:
A
x
=
b
A x=b
Ax=b
A
=
[
−
5
3
4
10
−
8
−
9
15
1
2
]
A= \begin{bmatrix} -5& 3&4 \\ 10 & -8 &-9\\ 15&1&2\end{bmatrix}
A=⎣
⎡−510153−814−92⎦
⎤
经过高斯消元得到
[
−
5
3
4
10
−
8
−
9
15
1
2
]
(
R
2
+
2
R
1
,
R
3
+
3
R
1
)
→
[
−
5
3
4
0
−
2
−
1
0
10
14
]
(
R
3
+
5
R
2
)
→
[
−
5
3
4
0
−
2
−
1
0
0
9
]
\begin{bmatrix} -5& 3&4 \\ 10 & -8 &-9\\ 15&1&2\end{bmatrix}(R_2+2R_1,R_3+3R_1) →\begin{bmatrix} -5& 3&4 \\ 0 & -2&-1\\ 0&10&14\end{bmatrix}(R_3 +5R_2)→ \begin{bmatrix} -5& 3&4 \\ 0 & -2&-1\\ 0&0&9\end{bmatrix}
⎣
⎡−510153−814−92⎦
⎤(R2+2R1,R3+3R1)→⎣
⎡−5003−2104−114⎦
⎤(R3+5R2)→⎣
⎡−5003−204−19⎦
⎤
所以,
U
=
[
−
5
3
4
0
−
2
−
1
0
0
9
]
U=\begin{bmatrix} -5& 3&4 \\ 0 & -2&-1\\ 0&0&9\end{bmatrix}
U=⎣
⎡−5003−204−19⎦
⎤
2. 求解L矩阵
L矩阵的下三角位置为,进行U分解时,消去某位置所乘系数的 相反数。
L
=
[
1
0
0
−
2
1
0
−
3
−
5
1
]
L=\begin{bmatrix} 1& 0&0 \\ -2 & 1&0\\ -3&-5&1\end{bmatrix}
L=⎣
⎡1−2−301−5001⎦
⎤
−
2
和
−
3
分别为
(
R
2
+
2
R
1
,
R
3
+
3
R
1
)
中
2
和
3
的相反数。
-2和-3分别 为(R_2+2R_1,R_3+3R_1)中2和3的相反数。
−2和−3分别为(R2+2R1,R3+3R1)中2和3的相反数。
−
5
为
(
R
3
+
5
R
2
)
中
5
的相反数。
-5为(R_3 +5R_2)中5的相反数。
−5为(R3+5R2)中5的相反数。
3. 验证
A = L U = [ 1 0 0 − 2 1 0 − 3 − 5 1 ] [ − 5 3 4 0 − 2 − 1 0 0 9 ] = [ − 5 3 4 10 − 8 − 9 15 1 2 ] A=LU=\begin{bmatrix} 1& 0&0 \\ -2 & 1&0\\ -3&-5&1\end{bmatrix} \begin{bmatrix} -5& 3&4 \\ 0 & -2&-1\\ 0&0&9\end{bmatrix}= \begin{bmatrix} -5& 3&4 \\ 10 & -8 &-9\\ 15&1&2\end{bmatrix} A=LU=⎣ ⎡1−2−301−5001⎦ ⎤⎣ ⎡−5003−204−19⎦ ⎤=⎣ ⎡−510153−814−92⎦ ⎤
4. 用途
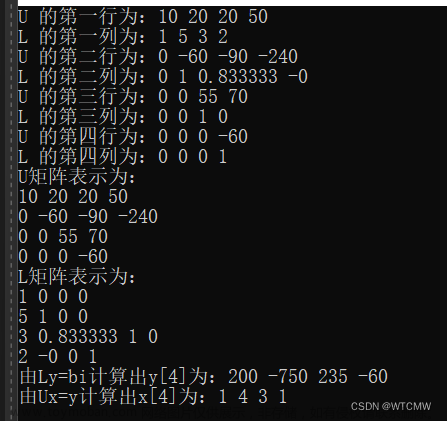
A x = b 可以写成 L ( U x ) = b 和 U x = y Ax=b可以写成L(Ux)=b和Ux=y Ax=b可以写成L(Ux)=b和Ux=y,即先求解 L ( y ) = b L(y)=b L(y)=b得到 y y y,再求解 ( U x ) = y (Ux)=y (Ux)=y得到 x x x,因为矩阵 L L L和 U U U都是三角矩阵,所以求解上述两个方程比直接求解 A x = b Ax=b Ax=b要简单。
L
(
y
)
=
b
L(y)=b
L(y)=b
[
1
0
0
2
1
0
3
4
1
]
[
y
1
y
2
y
3
]
=
[
12
24
12
]
⇒
[
y
1
y
2
y
3
]
=
[
12
0
−
24
]
\begin{bmatrix} 1& 0&0 \\ 2 & 1&0\\ 3&4&1\end{bmatrix} \begin{bmatrix} y_1\\y_2\\y_3\end{bmatrix}= \begin{bmatrix} 12\\24\\12\end{bmatrix}\Rightarrow \begin{bmatrix} y_1\\y_2\\y_3\end{bmatrix}=\begin{bmatrix} 12\\0\\-24\end{bmatrix}
⎣
⎡123014001⎦
⎤⎣
⎡y1y2y3⎦
⎤=⎣
⎡122412⎦
⎤⇒⎣
⎡y1y2y3⎦
⎤=⎣
⎡120−24⎦
⎤
(
U
x
)
=
y
(Ux)=y
(Ux)=y
[
2
2
2
0
3
3
0
0
4
]
[
x
1
x
2
x
3
]
=
[
12
0
−
24
]
⇒
[
x
1
x
2
x
3
]
=
[
6
6
−
6
]
\begin{bmatrix} 2& 2&2 \\ 0 & 3&3\\ 0&0&4\end{bmatrix}\begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix} 12\\0\\-24\end{bmatrix}\Rightarrow\begin{bmatrix} x_1\\x_2\\x_3\end{bmatrix}=\begin{bmatrix} 6\\6\\-6\end{bmatrix}
⎣
⎡200230234⎦
⎤⎣
⎡x1x2x3⎦
⎤=⎣
⎡120−24⎦
⎤⇒⎣
⎡x1x2x3⎦
⎤=⎣
⎡66−6⎦
⎤
部分主元法
部分主元消去法多了一个把最大的值调到主元位置的操作,可以提高计算精度。一般需要使用关联系数矩阵, P A = L U PA=LU PA=LU。
例如:
A
=
[
1
2
−
3
−
4
4
8
12
−
8
2
3
2
1
−
3
−
1
1
−
4
]
A=\begin{bmatrix} 1& 2&-3&-4 \\ 4 &8&12&-8\\2&3&2&1\\-3&-1&1&-4\end{bmatrix}
A=⎣
⎡142−3283−1−31221−4−81−4⎦
⎤
1. 加关联矩阵,找主元
进行行初等变换,找主元。
[
A
∣
p
]
=
[
1
2
−
3
−
4
4
8
12
−
8
2
3
2
1
−
3
−
1
1
−
4
1
2
3
4
]
→
[
4
8
12
−
8
1
2
−
3
−
4
2
3
2
1
−
3
−
1
1
−
4
2
1
3
4
]
\begin{bmatrix} A|p \end{bmatrix}= \left [ \begin{array}{c:c} \begin{matrix} 1& 2&-3&-4 \\ 4 &8&12&-8\\2&3&2&1\\-3&-1&1&-4\end{matrix}& \begin{matrix}1\\2\\3\\4\end{matrix} \end{array} \right ]→ \left [ \begin{array}{c:c} \begin{matrix} 4 &8&12&-8\\1& 2&-3&-4 \\ 2&3&2&1\\-3&-1&1&-4\end{matrix}& \begin{matrix}2\\1\\3\\4\end{matrix} \end{array} \right ]
[A∣p]=⎣
⎡142−3283−1−31221−4−81−41234⎦
⎤→⎣
⎡412−3823−112−321−8−41−42134⎦
⎤
2. 进行LU分解
强烈建议:每次进行初等行变换时,将系数的相反数提前写出,因为会受到初等行变换(交换两行)的影响。
[
A
∣
p
]
=
[
1
2
−
3
−
4
4
8
12
−
8
2
3
2
1
−
3
−
1
1
−
4
1
2
3
4
]
→
[
4
8
12
−
8
1
2
−
3
−
4
2
3
2
1
−
3
−
1
1
−
4
2
1
3
4
]
→
[
4
8
12
−
8
1
4
0
−
6
−
6
1
2
−
1
−
4
5
−
3
4
5
10
−
10
2
1
3
4
]
\begin{bmatrix} A|p \end{bmatrix}= \left [ \begin{array}{c:c} \begin{matrix} 1& 2&-3&-4 \\ 4 &8&12&-8\\2&3&2&1\\-3&-1&1&-4\end{matrix}& \begin{matrix}1\\2\\3\\4\end{matrix} \end{array} \right ]→ \left [ \begin{array}{c:c} \begin{matrix} 4 &8&12&-8\\1& 2&-3&-4 \\ 2&3&2&1\\-3&-1&1&-4\end{matrix}& \begin{matrix}2\\1\\3\\4\end{matrix} \end{array} \right ]→ \left [ \begin{array}{c:c} \begin{matrix} 4 &8&12&-8\\\frac{1}{4}& 0&-6&-6 \\ \frac{1}{2}&-1&-4&5\\\frac{-3}{4}&5&10&-10\end{matrix}& \begin{matrix}2\\1\\3\\4\end{matrix} \end{array} \right ]
[A∣p]=⎣
⎡142−3283−1−31221−4−81−41234⎦
⎤→⎣
⎡412−3823−112−321−8−41−42134⎦
⎤→⎣
⎡441214−380−1512−6−410−8−65−102134⎦
⎤ 文章来源:https://www.toymoban.com/news/detail-726830.html
文章来源:https://www.toymoban.com/news/detail-726830.html
3. 计算 A x = b Ax=b Ax=b
A x = b 可以写成 L ( U x ) = b 和 U x = y Ax=b可以写成L(Ux)=b和Ux=y Ax=b可以写成L(Ux)=b和Ux=y,通过先求 y y y,再求 x x x。文章来源地址https://www.toymoban.com/news/detail-726830.html
到了这里,关于【国科大——矩阵分析与应用】LU分解的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!