本文主要记录一下Float的一些基础知识。
在计算机界,有个规定叫IEEE754,它规定了如何以二进制的方式来存储10进制的数。
按照这个规定,单精度浮点数(float)这个数据类型所占内存大小为4个字节,也就是32位,所以单精度浮点数也叫32位浮点数,它在内存或硬盘中要占用32个比特。
字节就是存储数据的单位,并且是硬件所能访问的最小单位
1字节 = 8位
1K = 1024字节
二进制和十进制的互相转换
十进制与二进制的相互转换流程:
二进制转十进制:按权相加法。
十进制转二进制:除2取余,逆序排列。
二进制到十进制:
例一:10010 = 0 * 20 + 1 * 21 + 0 * 22 + 0 * 23 + 1 * 24 = 18 ;
例二:1010.11 = 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 + 1 * 2-1 = 10.5;
例三:1010.11 = 1 * 23 + 0 * 22 + 1 * 21 + 0 * 20 + 1 * 2-1 + 1 * 2-2 = 10.75
在小数点后的第n位,则乘以2-n
十进制到二进制:
18 / 2 = 9 … 0 ;
9 / 2 = 4 … 1 ;
4 / 2 = 2 … 0 ;
2 / 2 = 1 … 0 ;
1 / 2 = 0 … 1;
然后从下往上取余数,可得10010
以上的十进制数都是不带小数的,下面看看带小数的十进制数是如何与二进制互相转换的:
二进制转十进制:权相加法。
十进制转二进制:整数部分除2取余,逆序排列;小数部分使用乘 2 取整数位,顺序排列,直至小数点后为0;
二进制转十进制:
10.01 = 1 * 2-2 + 0 * 2-1 + 0 * 20 + 1 * 21 = 2.25
十进制转二进制:
整数部分:
2 / 2 = 1 … 0
1 / 2 = 0 … 1
小数部分:
0.25 * 2 = 0.5 … 0
0.5 * 2 = 1 … 1
整数部分从下往上取结果,是10。小数部分是从上往下取结果,是01,即10.01
二进制存储十进制的规范
举例说明,有个十进制的数10.75,它的二进制数是1010.11,再规范化后就是1.01011 * 23
规范化就是指把二进制数转化成“尾数 * 2指数”的形式,即把尾数的小数点放在第一位和第二位之间,然后保证第一位非0,再将尾数乘以2n。 上面的“1.01011”就是尾数,
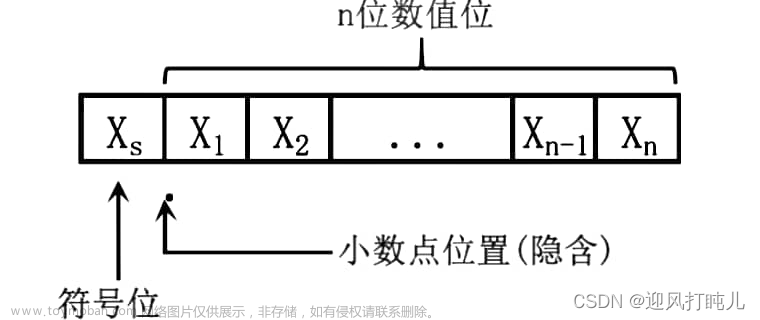
Float的存储结构
一个浮点数(Floating Point Number)由三个基本成分构成:
-
符号位(Sign)(占1位)
-
偏移指数位(阶码、指数)(Exponent)(占8位)
偏移指数位用来表示“规范化”后的指数值,上面以十进制数10.75为例,它的二进制数规范化后是1.01011 * 23,这里的“3”就是指数值。
为什么叫偏移呢,就是因为根据那个IEEE754规定,在单精度浮点数中,指数值的范围是-127~128。为了表示起来更加方便,浮点数的指数位都有一个固定的偏移量,偏移后的指数等于实际的指数加上偏移量,从而保证“偏移后的指数”总是一个非负整数,这样,指数位部分就不用为如何表示负数而担心了。
IEEE754规定了float浮点数的指数的偏移量是127。这里同样以上述的十进制数10.75为例:
二进制数规范化后是:1.01011 * 23
指数值是:3
则偏移指数值就是:3 + 127 = 130(加上127这个偏移量,避免出现负数)偏移指数位(130的二进制表示):1000 0010(8位比特的二进制)
摘录自:什么是浮点数?10分钟彻底掌握浮点数的底层原理 #安员外读书会
-
尾数位(Mantissa)(占23位)
就是小数点后面的那些小数
对于 32 位的单精度浮点型如下:
有 1位符号位(S),8位偏移指数位(P),23位尾数(M)
例:
十进制数16.5,转换为二进制数是:10000.1,规范化后是:1.00001 * 24
符号位(S):这个数是正数,所以为0
偏移指数位(P):看规范化后的式子,指数是4,所以就是偏移指数就是4+127=131。131的二进制形式是1000 0011,这就是8位的便宜指数位。
尾数(M):看规范化后的式子,小数部分是00001,这个就是尾数位了,但由于这个尾数部分总共有23位,所以还要在后面补18个0,所以完整的尾数部分是:0000 1000 0000 0000 0000 000
所以10进制的数字16.5在内存的表示为:
| 符号位(S) | 指数部分(P)(8位) | 尾数部分(M)(23位) |
|---|---|---|
| 0 | 1000 0011 | 0000 1000 0000 0000 0000 000 |
(参考来源https://blog.csdn.net/qq_34719188/article/details/83351918)
精度问题
float只能得到7位(包括整数部分和小数部分)精确数:
#include <stdio.h>
int main()
{
double a = 1.0;
float b = 2.3;
printf("a = %f \n",a/3);
printf("b = %f \n",b);
return0;
}
运行结果:
a = 0.333333
b = 2.300000
在C语言中,用%f输出单精度浮点数只有7位有效数字(整数部分和小数部分一共7位)
单精度浮点数的尾数部分用23位存储,加上默认的小数点前的1位1,2(23+1) = 16777216。
因为 107 < 16777216 < 108,所以说单精度浮点数的有效位数是7位
(摘自为何float有效位数为7位?)
float的小数可能会不精准:
#include <stdio.h>
int main()
{
float a = 1.1;
float b = 12.12;
float c = 123.123;
float d = 1234.1234;
float e = 12345.12345;
float f = 123456.123456;
printf("a = %f \n",a);
printf("b = %f \n",b);
printf("c = %f \n",c);
printf("d = %f \n",d);
printf("e = %f \n",e);
printf("f = %f \n",f);
return 0;
}
运行结果为:
a = 1.100000
b = 12.120000
c = 123.123001
d = 1234.123413
e = 12345.123047
f = 123456.125000
为什么精度会有问题:
根据上面十进制与二进制互相转换的方法,以十进制数2.1为例
转成二进制:
整数部分:
2 / 2 = 1 … 0
1 / 2 = 0 … 1
小数部分:
0.1 * 2 = 0.2 … 0
0.2 * 2 = 0.4 … 0
0.4 * 2 = 0.8 … 0
0.8 * 2 = 1.6 … 1
0.6 * 2 = 1.2 … 1
0.2 * 2 = 0.4 … 0
0.4 * 2 = 0.8 … 0
0.8 * 2 = 1.6 … 1
0.6 * 2 = 1.2 … 1
0.2 * 2 = 0.4 … 0
0.4 * 2 = 0.8 … 0
0.8 * 2 = 1.6 … 1
0.6 * 2 = 1.2 … 1
…
结果会发现十进制的0.1在二进制中并不能精确表示,只能用无限的小数位来逼近0.1。而计算机在存储小数时是有长度限制的(毕竟存储空间有限),所以会进行截取部分小数进行存储,从而导致计算机存储 2.1 这个十进制数字的值只能是个大概的值,而不是精确的值。
= 1.6 … 1
0.6 * 2 = 1.2 … 1
…
结果会发现十进制的0.1在二进制中并不能精确表示,只能用无限的小数位来逼近0.1。而计算机在存储小数时是有长度限制的(毕竟存储空间有限),所以会进行截取部分小数进行存储,从而导致计算机存储 2.1 这个十进制数字的值只能是个大概的值,而不是精确的值。
(参考来源:详谈浮点精度(float、double)运算不精确的原因)
补充
有一个浮点型变量,如何判断x的值是否为零
if(0 == x)
x是0
else
x不是0
上面这个判断方式对于浮点数来说是错误的,因为在float数据类型中,小数是以近似值来存储的
这里我有些不懂:
在一些教学视频中,说判断浮点数x是否为0应该这样写:
if(|x-0.000001| < 0.000001)
x是0
else
x不是0
再上网查,发现这样写的都是直接照搬,没说为啥,或者说了我也看不太懂的。
为什么是看x与0.000001的距离而不是看x与0.000000的距离,|x-0.000001| < 0.000001在数学上不是等价于0<x<0.000002吗
为什么不是
if(|x-0.000000| <= 0.000001)
x是0
else
x不是0
参考网上看到对我来说能看得懂,也能接受的是这样的:
参考了有一个浮点型变量 X,如何判断它是否为 0 ?用除法可以吗?中用户Uron的评论
再结合Comparison of a float with a value in C中,最后那里的Example no 2文章来源:https://www.toymoban.com/news/detail-727054.html
if(fabs(x) < 0.0000001)
x是0
else
x不是0
fabs()函数是用来求绝对值的,它在math.h这个头文件里面定义。文章来源地址https://www.toymoban.com/news/detail-727054.html
到了这里,关于C语言中的float(单精度浮点数)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!