图论——强连通分量详解！-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论——强连通分量详解！。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

写在前面：

本篇主要内容：

强连通分量等概念
Tarjan算法的过程与实现

强连通分量等概念：

首先我们要明白上面是连通。

连通：

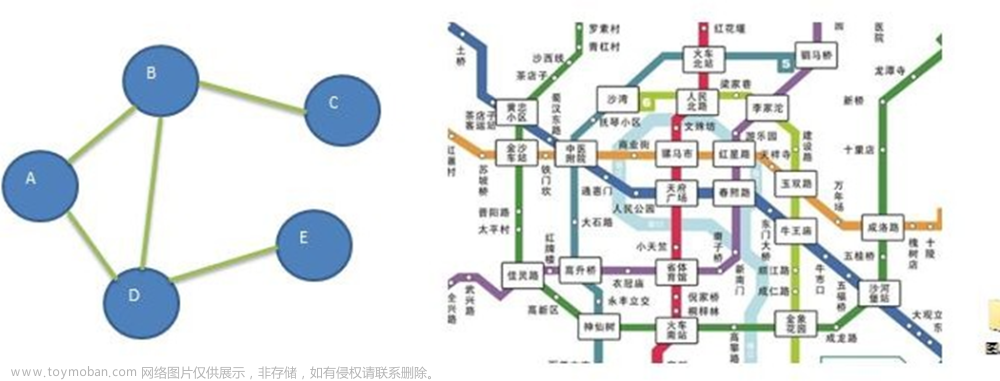
在一张图中任意两个点能互相到达。（举个例子）

强连通分量,图论,算法,数据结构

所以我们称上面的这个图是一个连通图！

接着我们在来理解什么是强连通。

强连通：

若一张有向图的节点两两互相可达，则称这张图是 强连通的。

和连通图的唯一不同就是连通图是无向图，而强连通是有向图。（再来个栗子）

强连通分量,图论,算法,数据结构

那明白了强连通，再看看什么是强连通分量。

强连通分量：

首先一张图很可能不是强连通图，但是它的子图可能是强强连通图，那我们称该子图是原图的强连通分量。（额。。。再给给栗子）

强连通分量,图论,算法,数据结构

例如上的图被框起来的每一个子图就是原图（整张图）的强连通分量！

ok到这里有关强连通分量等概念就讲完了。终于可以讲如何求强连分量了。

Tarjan算法的过程与实现：

过程：

我们考虑 DFS 生成树与强连通分量之间的关系。

若该子图是强连通图，那么从这个子图的根节点出发必定那再回到根。

说的专业一点就是：如果结点 u 是某个强连通分量在搜索树中遇到的第一个结点，那么这个强连通分量的其余结点肯定是在搜索树中以 u 为根的子树中。结点 u 被称为这个强连通分量的根。

具体地，在这个查找的过程中，可以对经过的结点标记，当发现某一节点连向的点正好已经被标记过，则说明找到了一条回路，而这个回路上的所有点构成一个强连通分量。

为了保存这个强连通分量，我们需要知道这条路上有哪些点，而此时，栈就是一种适合该算法的数据结构。对于每次搜索的点，我们都加入栈中，遇到回路时，在把栈中的元素逐个弹出，记录它们的起始结点，直到栈中弹出的元素正好是起始结点时，结束弹栈，继续搜索其它强连通分量。在这个过程中，所有的点和都有的边都被遍历了一次，所以最终的时间复杂度为O ( N + E )

——图论——强连通分量（Tarjan算法)_上总介的博客-CSDN博客

额。。。学习了一下dalao

实现：

在 Tarjan 算法中为每个结点 u 维护了以下几个变量：

dfn[u]：深度优先搜索遍历时结点 u 被搜索的次序。（就是时间戳）
low[u]：在 u 的子树中能够回溯到的最早的已经在栈中的结点。
subtree[u]：表示以 u 为根的子树。
instack：表示是否在栈中的数组。

再来n个栗子：

强连通分量,图论,算法,数据结构

不好意思图画太大了所以截的有点模糊，呃呃呃将就着看吧！

强连通分量,图论,算法,数据结构

好吧我画累了，上面这张图是最终版。。。（啊！创作不容易点个赞吧QA）

再说明一点：

对于一个连通分量图，我们很容易想到，在该连通图中有且仅有一个 u 使得 dfn[u]=low[u]。该结点一定是在深度遍历的过程中，该连通分量中第一个被访问过的结点，因为它的 dfn 和 low 值最小，不会被该连通分量中的其他结点所影响。

因此，在回溯的过程中，判定 dfn[u]=low[u] 是否成立，如果成立，则栈中 u 及其上方的结点构成一个 SCC（强连通分量）。

好好体会一下。

代码：

终于啊！写了5个小时了.........

伪代码：

tarjan(u){
	dfn[u]=low[u]=++Index
	for each(u,v) in E
		if(v is not visted){
			tarjan(v)
			low[u]=min(low[u],low[v])
		}
		else if(v in s)
			low[u]=min(low[u],dfn[v])
	if(dfn[u]==low[u])
		repeat
			v=stack.pop
			print v
		until(u==v)
}

c++Tarjan模板：

#include<bits/stdc++.h>

using namespace std;
int n,m,cnt,cntb;
vector<int> edge[101];
vector<int> belong[101];
bool instack[101];
int dfn[101],low[101];
stack<int> s;
void Tarjan(int u){
	++cnt;
	dfn[u]=low[u]=cnt;
	s.push(u);
	instack[u]=true;
	for(int i=0;i<edge[u].size();i++){
		int v=edge[u][i];
		if(!dfn[v]){
			Tarjan(v);
			low[u]=min(low[u],low[v]);
		}
		else if(instack[v]){
			low[u]=min(low[u],dfn[v]);
		}
	}
	if(dfn[u]==low[u]){
		++cntb;
		int node;
		do{
			node=s.top();
			s.pop();
			instack[node]=false;
			belong[cntb].push_back(node);
		}while(node!=u);
	}
}
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++){
		int u,v;
		scanf("%d%d",&u,&v);
		edge[u].push_back(v);
	}
	Tarjan(1);
	printf("id :");
	for(int i=1;i<=n;i++){
		printf("%d ",i);
	}
	printf("\n");
	printf("dfn :");
	for(int i=1;i<=n;i++){
		printf("%d ",dfn[i]);
	}
	printf("\n");
	printf("low :");
	for(int i=1;i<=n;i++){
		printf("%d ",low[i]);
	}
	printf("\n");
	for(int i=1;i<=cntb;i++){
		printf("SCG %d :",i);
		for(int j=0;j<belong[i].size();j++){
			printf("%d ",belong[i][j]);
		}
		printf("\n");
	}
	return 0;
}

可以试试样例：

运行结果：

强连通分量,图论,算法,数据结构

例题：

【模板】缩点 - 洛谷

题目描述：

给定一个 n 个点 m 条边有向图，每个点有一个权值，求一条路径，使路径经过的点权值之和最大。你只需要求出这个权值和。

允许多次经过一条边或者一个点，但是，重复经过的点，权值只计算一次。

题解：

根据题目意思，我们只需要找出一条点权最大的路径就行了，不限制点的个数。那么考虑对于一个环上的点被选择了，一整条环是不是应该都被选择，这一定很优，能选干嘛不选。很关键的是题目还允许我们重复经过某条边或者某个点，我们就不需要考虑其他了。因此整个环实际上可以看成一个点（选了其中一个点就应该选其他的点）——luogu题解

代码（有注释）：

#include<bits/stdc++.h>

using namespace std;

const int N=1e4+10,M=1e5+10;

struct point{
	int nxt;
	int to;
	int from;
}e_1[M],e_2[M];

int val[N];//存储点权
int head_1[N],head_2[N];
int cnt_1,cnt_2;
int n,m;//点数，边数
int dfn[N],low[N];
int sta[N],top;//栈
int ind;//遍历顺序，时间戳
int inDegree[N];//入度
int d[N];//以i为结尾的路径值
int sd[N];//每个结点在连通分量中的根结点
bool vis[N];

int read(){
	int x=0,w=1;
	char ch=0;
	while(ch<'0' || ch>'9'){
		if(ch=='-') w=-1;
		ch=getchar();
	}
	while(ch>='0' && ch<='9'){
		x=x*10+(ch-'0');
		ch=getchar();
	}
	return x*w;
}
void add(int x,int y){
	e_1[++cnt_1].from=x;
	e_1[cnt_1].to=y;
	e_1[cnt_1].nxt=head_1[x];
	head_1[x]=cnt_1;
}
void Tarjan(int x){
	dfn[x]=low[x]=++ind;
	sta[++top]=x;
	vis[x]=1;
	for(int i=head_1[x];i;i=e_1[i].nxt){
		int y=e_1[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(vis[y]){
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(low[x]==dfn[x]){
		int y;
		while(y=sta[top--]){
			sd[y]=x;
			vis[y]=0;
			if(y==x) break;
			val[x]+=val[y];//把连通分量中的其他结点的权值加到根结点上
		}
	}
}
int ask(){
	queue<int> q;
	for(int i=1;i<=n;i++){
		if(i==sd[i] && inDegree[i]==0){
			q.push(i);
			d[i]=val[i];
		}
	}
	int u,v;
	while(!q.empty()){
		u=q.front();
		q.pop();
		for(int i=head_2[u];i;i=e_2[i].nxt){
			v=e_2[i].to;
			d[v]=max(d[v],d[u]+val[v]);
			inDegree[v]--;
			if(inDegree[v]==0){
				q.push(v);
			}
		}
	}
	int ans=0;
	for(int i=1;i<=n;i++){
		ans=max(ans,d[i]);
	}
	return ans;
}
int main(){
	n=read();m=read();
	for(int i=1;i<=n;i++){
		val[i]=read();
	}
	//建图
	int u,v;
	for(int i=1;i<=m;i++){
		u=read();v=read();
		add(u,v);
	}
	//Tarjan
	for(int i=1;i<=n;i++){
		if(!dfn[i])
			Tarjan(i);
	}
	//重新建图
	for(int i=1;i<=m;i++){
		u=sd[e_1[i].from];
		v=sd[e_1[i].to];
		if(u!=v){
			e_2[++cnt_2].from=u;
			e_2[cnt_2].to=v;
			e_2[cnt_2].nxt=head_2[u];
			head_2[u]=cnt_2;
			inDegree[v]++;
		}
	}
	printf("%d",ask());
	return 0;
}